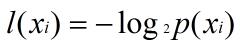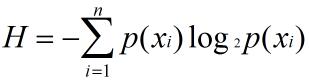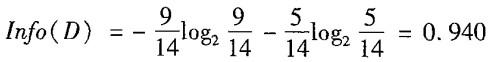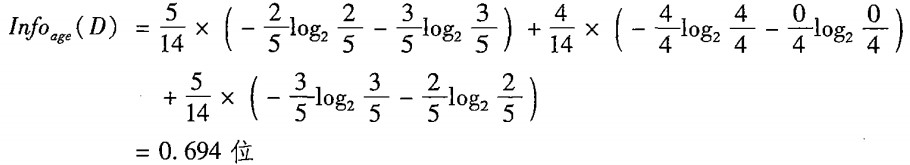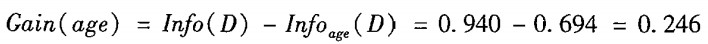《機器學習實戰》第三章:決策樹(1)基本概念
有半個月沒來了。
最近一段時間...大多在忙專案組的事(其實就是改一改現有程式碼的bug,不過也挺費勁的,畢竟程式碼不是自己寫的)。另外就是自己租了幾臺美帝的vps,搭了$-$的伺服器 ,效果還不錯。自己搭的話就不用去買別人的服務了,不過租vps畢竟還是要成本的,光用來番茄的話,價效比仍然比不過各路山寨奸商。
,效果還不錯。自己搭的話就不用去買別人的服務了,不過租vps畢竟還是要成本的,光用來番茄的話,價效比仍然比不過各路山寨奸商。
然而我用學校郵箱註冊了Github,會送一個學生大禮包,裡面有些vps服務商的合作專案, 各種優惠。像aws的兩個美國節點就有一年的免費使用權;Digital Ocean還送50刀的credit,也能用挺久了。話說回來,還是得給伺服器找點“正事兒”來跑,不然有點浪費了。
------------------------------------------------------------------------------------------------
扯遠了。迴歸正題,決策樹。
這個玩意其實我並不太陌生。《人工智慧》《資料探勘》等幾門課裡面都動手實踐過。還做過決策樹的“增強版”——隨機森林。這本書是用python實現的決策樹,程式碼比較簡潔。
------------------------------------------------------------------------------------------------
決策樹(Decision Tree)
(1)是個基本的【分類】演算法。
(2)基本思想:決策樹是一種樹結構,其中的每個內部節點代表對某一特徵的一次測試,每條邊代表一個測試結果,葉節點代表某個類或類的分佈。決策樹的決策過程需要從決策樹的根節點開始,待測資料與決策樹中的特徵節點進行比較,並按照比較結果選擇選擇下一比較分支,直到葉子節點作為最終的決策結果。
(3)舉個例子吧:
比如,兩個同班同學A和B,玩一個遊戲。A頭腦中想著班上的一個同學,讓B來猜是誰。B可以不斷地通過向A提問,來逐漸縮小猜測範圍,比如“這個人是男生還是女生”,“這個人身高是160以下,是160-170,是170-180,還是180以上”,“這個人有沒拿過國家獎學金”等等,直到剩下一個或很有限個幾個候選人。
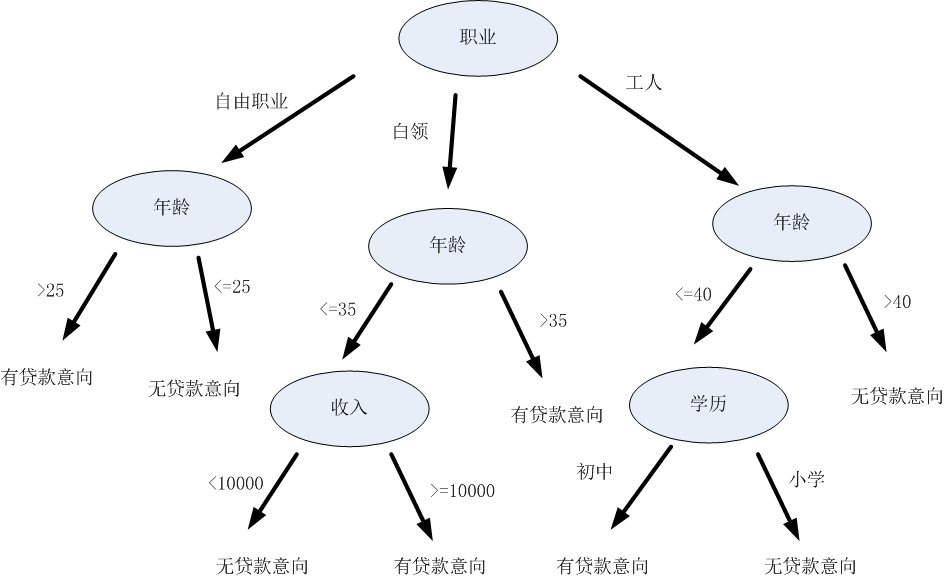
嗯...這個過程其實類似於決策樹的決策過程,也就是拿到一條待分類的資料,給他進行分類:從決策樹的根節點開始,按照一定順序驗證這條資料的特徵。在每個特徵節點上,按照該資料特徵值對應的分類,順著決策樹的邊,進入下一層節點,直到到達葉節點,得到最終的決策結果(即標籤)。例如...有一家貸款機構拿到了一個人的個人資訊(可能是資訊洩露了),然後想根據下面這棵決策樹,判斷這個人有沒貸款意向,從而決定要不要給他打騷擾電話:
決策樹的構造過程,其實就是他的“機器學習過程”,也就是機器根據資料集建立規則的過程。什麼規則?就是在樹的每一個節點上,究竟該選擇哪一個資料屬性,來把這個節點中的資料集分開呢?比如上面那個猜同學的遊戲,是先問“性別”,還是先問“身高”,才能達到縮小猜測範圍的最佳效果呢?
等下會介紹。
(4)優點:複雜度不高
缺點:可能會產生過度匹配的問題
適用資料型別:離散型,連續型。
------------------------------------------------------------------------------------------------
資訊增益(Information Gain)、熵(Entropy)
回到剛才那個問題,在決策樹的每個節點上,究竟是選擇哪個特徵來把這個節點裡的資料集劃分開呢?
劃分資料集的大原則是:將無序的資料變得更加有序。
那麼,怎樣度量資料有序還是無序?一種方法就是使用資訊理論來度量。
在劃分資料集之前之後,資訊發生的變化稱為資訊增益。我們希望計算出每個特徵值劃分資料集獲得的資訊增益。那麼,資訊增益最高的特徵就是最好的選擇。墜吼滴!
對於一個資料集合而言,資訊的度量方式稱為夏農熵,或簡稱為熵。熵越大,說明資料集越混亂、越無序。一個數據集合,再劃分前、劃分後,熵的變化,就是資訊增益了。資訊增益越大,說明資料集合劃分之後,有序程度的增加量越大。
那麼怎樣計算熵呢?熵定義為資訊的期望值。如果待分類的事務可能劃分在多個分類之中,假設 Xi是其中的一個類,則符號 Xi 的資訊定義為:
其中,p(Xi) 是選擇該分類的概率。
為了計算熵,我們需要計算所有類別的所有可能值所包含的資訊期望值:
其中,n是分類的數目。
還是來舉個栗子:
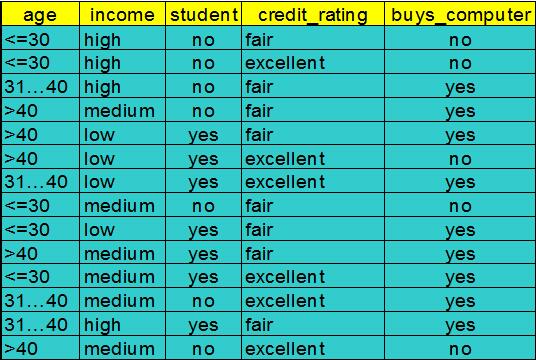
這個例子取自於《資料探勘:概念與技術》。前4列:age(年齡)、income(收入)、student(是否是學生)、credit_rating(信用評級)是特徵值。最後一列:buys_computer(是否買電腦)是分類(也就是標籤)。
這裡有14條資料,他們現在處於同一個節點之中,我們先用4個特徵中的某一個,來劃分它們。先算當前沒劃分時的熵:
根據最後一列的標籤,這對資料有兩個分類:yes / no。這14條資料裡,有9條的分類是yes,5條是no。那麼按上面的公式計算,當前資料集合的熵就是0.940。
接下來,我們看看按照4種特徵劃分這個資料集合後,熵變成了多少。
首先是age(年齡)。如果按照age來分,那麼會分出3個子資料集,因為age有3種不同的特徵值:<=30,31-40,>40。
<=30:一共5條資料,其中2條yes,3條no
30-40:一共4條資料,其中4條yes,0條no
>40:一共5條資料,其中3條yes,2條no
那麼,按照age來分的話,劃分後的熵就是:
注意,這裡計算的是劃分後3個子資料集的熵的總和,每個子資料集的熵之前還乘上了一個權重,也就是這個子資料集的概率。
然後,拿劃分前的熵減劃分後的熵,就得到了資訊增益:
接下來算按照income、student、credit_rating來劃分的情況,過程一樣的:
Infoincome(D) = 4/14 * [ -2/4*log(2/4) - 2/4*log(2/4)] + 6/14* [ -4/6*log(4/6) - 2/6*log(2/6)] + 4/14* [ -3/4*log(3/4) - 1/4*log(1/4)]
Gain(income) =0.029
Infostudent(D) = 7/14 * [ -3/7*log(3/7) - 4/7*log(4/7)] + 7/14* [ -1/7*log(1/7) - 6/7*log(6/7)]
Gain(student) =0.151
Infocredit_rating(D) = 6/14 * [ -3/6*log(3/6) - 3/6*log(3/6)] + 8/14 * [ -6/8*log(6/8)- 2/8*log(2/8)]
Gain(credit_rating) = 0.048
比較之後,發現按照 age 劃分,資訊增量是最大的。所以在這個節點,我們決定按照 age 來進行劃分。
哦對了,以上的演算法是ID3演算法。它傾向於選擇具有大量值的屬性,即值比較分散的屬性。除此之外還有C4.5演算法。它引入了增益率(gain ratio)的概念,具體就不介紹了。
嗯,決策樹最核心的部分應該就是這些了。下一篇部落格上程式碼。
相關推薦
《機器學習實戰》第三章:決策樹(1)基本概念
有半個月沒來了。 最近一段時間...大多在忙專案組的事(其實就是改一改現有程式碼的bug,不過也挺費勁的,畢竟程式碼不是自己寫的)。另外就是自己租了幾臺美帝的vps,搭了$-$的伺服器 ,效果還不錯。自己搭的話就不用去買別人的服務了,不過租vps畢竟還是要成本的,光用來番茄
《機器學習實戰》第五章:Logistic迴歸(1)基本概念和簡單例項
最近感覺時間越來越寶貴,越來越不夠用。不過還是抽空看了點書,然後整理到部落格來。 加快點節奏,廢話少說。 Keep calm & carry on. ----------------------------------------------------------
機器學習實戰第三章——決策樹(原始碼解析)
機器學習實戰中的內容講的都比較清楚,一般都能看懂,這裡就不再講述了,這裡主要是對程式碼進行解析,如果你很熟悉python,這個可以不用看。 #coding=utf-8 ''' Created on 2016年1月5日 @author: ltc ''' from mat
機器學習實戰第三章——決策樹程式
在閱讀理解決策樹之後,按照《機器學習實戰》的程式碼,實現ID3決策樹 程式如下: from math import log def calcShannonEnt(dataSet): numEntries = len(dataSet) labelCounts
機器學習實戰—第9章:樹迴歸 程式程式碼中的小錯誤
提示:本人程式碼執行在Python3的環境下 1、程式清單9-1: 應改為: list(map(float, curLine)) 解釋:map()返回結果是一個Iterator,Iterator是惰性序列,因此通過list()函式讓它把整個序列都計算出來並返回
機器學習實戰—第5章:Logistic迴歸中程式清單5-1中的數學推導
如圖中梯度上升法給出的函式程式碼。 假設函式為: 1、梯度上升演算法(引數極大似然估計值): 通過檢視《統計學習方法》中的模型引數估計,分類結果為類別0和類別1的概率分別為: 則似然函式為: 對數似然函式為: 最大似然估計求使得對數似然函式取最大值時的引數
【機器學習實戰—第4章:基於概率論的分類方法:樸素貝葉斯】程式碼報錯(python3)
1、報錯:UnicodeDecodeError: ‘gbk’ codec can’t decode byte 0xae in position 199: illegal multibyte sequence 原因:這是檔案編碼的問題,檔案中有非法的多位元組字元。 解決辦法:開啟Ch04\
機器學習實戰第三章程式碼3-2註釋
按照給定特徵劃分資料集 ""splitDataSet函式引數: dataSet為輸入資料集,包含label值;axis為每行的第axis元素,value為對應元素的值,即特徵值。 函式功能:找出所有
《深度實踐Spark機器學習 》第11章 pyspark決策樹模型
由於此書不配程式碼,以下程式碼都是本寶寶在ipynb測試過的,執行環境為hdp2.6.2和Anaconda2。完整ipynb和py程式碼地址:https://gitee.com/iscas/deep_spark_ml/tree/master11.3 資料載入刪除標題sed 1
機器學習實戰 第九章回歸樹錯誤
最近一直在學習《機器學習實戰》這本書。感覺寫的挺好,並且在網上能夠輕易的找到python原始碼。對學習機器學習很有幫助。 最近學到第九章樹迴歸。發現程式碼中一再出現問題。在網上查了下,一般的網上流行的錯誤有兩處。但是我發現原始碼中的錯誤不止這兩處,還有個錯誤在
[完]機器學習實戰 第六章 支援向量機(Support Vector Machine)
[參考] 機器學習實戰(Machine Learning in Action) 本章內容 支援向量機(Support Vector Machine)是最好的現成的分類器,“現成”指的是分類器不加修改即可直接使用。基本形式的SVM分類器就可得到低錯
【SpringCloud Greenwich版本】第三章:服務消費者(Feign)
一、SpringCloud版本 本文介紹的Springboot版本為2.1.1.RELEASE,SpringCloud版本為Greenwich.RC1,JDK版本為1.8,整合環境為IntelliJ IDEA 二、Feign介紹 Feign是一個宣告式的Web服務客戶端。這使得W
讀書筆記--《程式設計師的自我修養》第4章:靜態連結(1)
本章以 如何將a.c檔案與b.c檔案連結成一個可執行檔案 來探討如何進行靜態連結 其中a.c和b.c檔案如下: a.c檔案 extern int shared; int main() { int a = 100; swap(&a,&shared);
《機器學習》第三章 決策樹學習 筆記加總結
分類問題 子集 觀察 組成 cas 普通 重復 1.0 需要 《機器學習》第三章 決策樹學習 決策樹學習方法搜索一個完整表示的假設空間,從而避免了受限假設空間的不足。決策樹學習的歸納偏置是優越選擇較小的樹。 3.1.簡介 決策樹學習是一種逼近離散值目標函數的方法,在這種方法
機器學習實戰第8章預測數值型數據:回歸
矩陣 向量 from his sca ima 用戶 targe 不可 1.簡單的線性回歸 假定輸入數據存放在矩陣X中,而回歸系數存放在向量W中,則對於給定的數據X1,預測結果將會是 這裏的向量都默認為列向量 現在的問題是手裏有一些x
機器學習實戰(第三篇)-決策樹簡介
我們經常使用決策樹處理分類問題,近來的調查表明決策樹也是最經常使用的資料探勘演算法。它之所以如此流行,一個很重要的原因就是使用者基本上不用瞭解機器學習演算法,也不用深究它是如何工作的。 如果你以前沒有接觸過決策樹,不用擔心,它的概念非常簡單。即使不知道它也可以通
機器學習實戰(第三篇)-決策樹構造
首先我們分析下決策樹的優點和缺點。優點:計算複雜度不高,輸出結果易於理解,對中間值的卻是不敏感,可以處理不相關特徵資料;缺點:可能會產生過度匹配問題。適用資料型別:數值型和標稱型。 本篇文章我們將一步步地構造決策樹演算法,並會涉及許多有趣的細節。首先我們先討論數
程式碼註釋:機器學習實戰第2章 k-近鄰演算法
寫在開頭的話:在學習《機器學習實戰》的過程中發現書中很多程式碼並沒有註釋,這對新入門的同學是一個挑戰,特此貼出我對程式碼做出的註釋,僅供參考,歡迎指正。 1、匯入資料: #coding:gbk from numpy import * import operator de
機器學習實踐-第三章 決策樹
計算給定資料集的夏農熵from math import log import operator def calcShannonEnt(dataSet): numEntries = len(dat
程式碼註釋:機器學習實戰第12章 使用FP-growth演算法來高效發現頻繁項集
寫在開頭的話:在學習《機器學習實戰》的過程中發現書中很多程式碼並沒有註釋,這對新入門的同學是一個挑戰,特此貼出我對程式碼做出的註釋,僅供參考,歡迎指正。 #coding:gbk #作用:FP樹中節點的類定義 #輸入:無 #輸出:無 class treeNode: