上一節中,我們介紹了Harris角點檢測。角點在影象旋轉的情況下也可以檢測到，但是如果減小(或者增加)影象的大小，可能會丟失影象的某些部分，甚至導致檢測到的角點發生改變。這樣的損失現象需要一種與影象比例無關的角點檢測方法來解決。尺度不變特徵變換(Scale-Invariant Feature Transform,SIFT)可以解決這個問題。我們使用一個變換來進行特徵變換，並且該變換會對不同的影象尺度輸出相同的結果。

到底什麼是SIFT演算法？通俗一點說，SIFT演算法利用DoG(差分高斯)來提取關鍵點(或者說成特徵點)，DoG的思想是用不同的尺度空間因子(高斯正態分佈的標準差$\sigma$)對影象進行平滑，然後比較平滑後圖像的區別，差別大的畫素就是特徵明顯的點，即可能是特徵點。對得到的所有特徵點，我們剔除一些不好的，SIFT運算元會把剩下的每個特徵點用一個128維的特徵向量進行描述。

由上，易知，一幅影象經過SIFT演算法後可以表示為一個128維的特徵向量集。

SIFT具有一下特徵：

• SIFT特徵，對旋轉、尺度縮放、亮度變化等保持不變性，對視角變換、仿射變化、噪聲也保持一定程度的穩定性，是一種非常優秀的區域性特徵描述演算法；
• 獨特性好，資訊量豐富，適用於海量特徵庫進行快速、準確的匹配；
• 多量性，即使是很少幾個物體也可以產生大量的SIFT特徵；
• 高速性，經優化的SIFT匹配演算法甚至可以達到實時性的要求；
• 擴充套件性，可以很方便的與其他的特徵向量進行聯合。

一 使用DoG和SIFT進行特徵提取和描述

我們先用OpenCV庫函式演示一下DoG和SIFT特徵提取的效果,然後再來講述一下SIFT的原理。

我們先來介紹一下Different of Gaussians(DoG)，DoG是對同一圖象使用不同高斯濾波器作差所得到的結果。DoG操作的最終結果會得到感興趣的區域(關鍵點)，這將通過SIFT來進行特徵描述。

我們來看看如何通過SIFT得到充滿角點和特徵的影象：

# -*- coding: utf-8 -*-
"""
Created on Wed Aug 22 16:53:16 2018

@author: lenovo
"""

'''
SIFT演算法
'''
import cv2
import numpy as np

img = cv2.imread('./image/cali.bmp')
img 
 
= cv2.resize(img,dsize=(600,400))
#轉換為灰度影象
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
#建立一個SIFT物件
sift = cv2.xfeatures2d.SIFT_create()
#SIFT物件會使用DoG檢測關鍵點，並且對每個關鍵點周圍的區域計算特徵向量。該函式返回關鍵點的資訊和描述符
keypoints,descriptor = sift.detectAndCompute(gray,None)
print(type(keypoints),len(keypoints),keypoints[0])
print(descriptor.shape)
#在影象上繪製關鍵點
img = cv2.drawKeypoints(image=img,keypoints = keypoints,outImage=img,color=(255,0,255),flags=cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)
#顯示影象
cv2.imshow('sift_keypoints',img)
cv2.waitKey(0)
cv2.destroyAllWindows()

我們首先建立了一個SIFT物件，SIFT物件會使用DoG檢測關鍵點，並且對每個關鍵點周圍區域計算特徵向量。detectAndCompute()函式會返回關鍵點資訊(每一個元素都是一個物件，有興趣的可以看一下OpenCV原始碼)和關鍵點的描述符。然後，我們在影象上繪製關鍵點，並顯示出來。

 上面我們用到了一個函式，下面來介紹一下：

cv2.drawKeypoints(image,keypoints,outImage[,color[,flags]])

 引數描述：

image：原始影象，可以使三通道或單通道影象；

keypoints：特徵點集合list，向量內每一個元素是一個KeyPoint物件，包含了特徵點的各種屬性資訊；

outImage：特徵點繪製的畫布影象，可以是原影象；

color：顏色設定，繪製的特徵點的顏色資訊，預設繪製的是隨機彩色；

flags：特徵點的繪製模式，其實就是設定特徵點的哪些資訊需要繪製，哪些不需要繪製，有以下幾種模式可選：

•  cv2.DRAW_MATCHES_FLAGS_DEFAULT：建立輸出影象矩陣，使用現存的輸出影象繪製匹配對和特徵點，對每一個關鍵點只繪製中間點；
• cv2.DRAW_MATCHES_FLAGS_DRAW_OVER_OUTIMG：不建立輸出影象矩陣，而是在輸出影象上繪製匹配對；
• cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS：對每一個特徵點繪製帶大小和方向的關鍵點圖形；
• cv2.DRAW_MATCHES_FLAGS_NOT_DRAW_SINGLE_POINTS：單點的特徵點不被繪製；

我們傳入了DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS標誌位，表明對影象每個關鍵點都繪製圓圈(大小)和方向。

二 SIFT演算法原理

1、SIFT特徵檢測的步驟

1. 尺度空間的極值檢測：搜尋所有高斯尺度空間上的影象，通過高斯差分函式(DoG)來識別潛在的對尺度和選擇不變的興趣點。
2. 關鍵點的定位和過濾：在每個候選的位置上，通過一個擬合精細模型來確定位置尺度，關鍵點的選取依據他們的穩定程度。
3. 特徵方向賦值：基於影象區域性的梯度方向，分配給每個關鍵點位置一個或多個方向，後續的所有操作都是對於關鍵點的方向、尺度和位置進行變換，從而提供這些特徵的不變性。
4. 特徵點描述：在每個特徵點周圍的鄰域內，在選定的尺度上測量影象的區域性梯度，這些梯度被變換成一種表示，這種表示允許比較大的區域性形狀的變形和光照變換。

2、尺度空間

在一定的範圍內，無論物體是大還是小，人眼都可以分辨出來。然而計算機要有相同的能力卻不是那麼簡單的事情，在未知的場景中，計算機視覺並不能提供物體的尺度大小，其中的一個方法就是把物體不同尺寸下的影象都提供給機器，讓機器能夠對物體再不同的尺度下有一個統一的認知。在建立統一認知的過程中，要考慮的就是影象在不同的尺度下都存在的特徵點。

2.1 多解析度影象金字塔

在早期影象的多尺度通常使用影象金字塔表述形式。影象金字塔是同一圖象在不同的解析度下得到的一組結果，其生成過程一半包含兩個步驟：

1、對原始影象進行平滑出來；

2、對處理後的影象進行降維取樣(通常是水平、垂直方向的1/2)；降維取樣後得到一系列尺寸不斷縮小的影象。顯然，一個傳統的金字塔中，每一層的影象是其上一層影象長、高的各一半。多解析度的影象金字塔雖然生成簡單，但其本質是降維取樣，影象的區域性特徵則難以保持，也就是無法保持特性的尺度不變性。

2.2 高斯尺度空間

我們還可以通過影象的模糊程度來模擬人在距離物體遠近時物體在視網膜上的成像過程，距離物體越近其尺寸越大影象也越清晰，這就是高斯尺度空間，使用不同的引數模糊影象(保持解析度不變)，是尺度空間的另一種表現形式。

我們知道影象和高斯函式進行卷積運算能夠對影象進行模糊，使用不同的"高斯核"可得到不同模糊程度影象。

高斯核函式$G(x,y,σ)$(二維高斯函式)的公式可以寫成：

$$G(x,y,σ)=\frac{1}{2\pi σ^2}e^{\frac{x^2+y^2}{2σ^2}}$$

$σ$稱為尺度空間因子，它是高斯正太分佈的標準差，反映了影象被模糊的程度，其值越大影象越模糊，對應的尺度也就越大。

在二維空間中，這個公式生成的曲面的等高線是從中心開始呈正態分佈的同心圓，如圖所示。分佈不為零的畫素組成的卷積矩陣與原始影象做變換。每個畫素的值都是周圍相鄰畫素值的加權平均。原始畫素的值有最大的高斯分佈值，所以有最大的權重，相鄰畫素隨著距離原始畫素越來越遠，其權重也越來越小。這樣進行模糊處理比其它的均衡模糊濾波器更高地保留了邊緣效果。

一副影象其高斯尺度空間可由其和不同的高斯卷積得到：

$$L(x,y,σ)=G(x,y,σ)*I(x,y)$$

$L(x,y,σ)$代表著影象的高斯尺度空間。下圖為影象取不同$\sigma$值得到的高斯尺度空間：

構建尺度空間的目的是為了檢測出在不同的尺度下都存在的特徵點，而檢測特徵點較好的運算元是$\sigma^2\nabla^2G$(高斯拉普拉斯,LoG，影象的二階導數)，是由2002年Mikolajczyk在詳細的實驗比較中發現的，同其它的特徵提取函式，例如：梯度，Hessian或Harris角特徵比較，能夠產生最穩定的影象特徵。

而Lindeberg早在1994年就發現高斯差分函式（Difference of Gaussian ，簡稱DOG運算元）與尺度歸一化的高斯拉普拉斯函式$\sigma^2\nabla^2G$非常近似。使用LoG雖然能較好的檢測到影象中的特徵點，但是其運算量過大，通常可使用DoG(差分高斯,Difference of Gaussina)來近似計算LoG。其中$D(x,y,\sigma)$和$\sigma^2\nabla^2G$的關係可以從如下公式推導得到：$$\frac{\partial{G}}{\partial{\sigma}}=\sigma^2\nabla^2G$$

利用差分近似代替微分，則有：$$\sigma^2\nabla^2G=\frac{\partial{G}}{\partial{\sigma}}≈\frac{G(x,y,k\sigma)-G(x,y,\sigma)}{k\sigma-\sigma}$$    

因此有：$$G(x,y,k\sigma)-G(x,y,\sigma)≈(k-1)\sigma^2\nabla^2G$$

其中k-1是個常數，並不影響極值點位置的求取。高斯拉普拉斯和高斯差分的比較如下：

如圖所示，紅色曲線表示的是高斯差分運算元，而藍色曲線表示的是高斯拉普拉斯運算元。Lowe使用更高效的高斯差分運算元代替拉普拉斯運算元進行極值檢測，設$k$為相鄰兩個高斯尺度空間的比例因子，則DoG的定義:

$$D(x,y,σ)=[G(x,y,kσ)-G(x,y,σ)]*I(x,y)$$ $$=L(x,y,kσ)-L(x,y,σ)$$

其中，$L(x,y,σ)$是影象的高斯尺度空間。

從上式可以知道，將相鄰的兩個高斯空間的影象相減就得到了DoG的響應影象。為了得到DoG影象,先要構造高斯尺度空間,而高斯的尺度空間可以在影象金字塔降維取樣的基礎上加上高斯濾波得到,也就是對影象金字塔的每層影象使用不同的尺度引數$\sigma$進行高斯模糊，使每層金字塔有多張高斯模糊過的影象，然後我們把得到的同一尺寸大小的影象劃分為一組。

易知，高斯金字塔有多組(如上圖)，每組又有多層。一組中的多個層之間的尺度是不一樣的(也就是使用的高斯引數$\sigma$是不同的)，相鄰兩層之間的尺度相差一個比例因子$k$，如果每組有$S$層，則$k=2^{\frac{1}{S}}$。上一組影象的最低層圖象是由下一組中尺度為$2\sigma$的影象進行因子為2的降維取樣得到的(高斯金字塔先底層建立)。高斯金字塔構建完成後，將相鄰的高斯金字塔相減就得到了DoG金字塔。

高斯金字塔的組數一般是:

$$O=[log_2min(m,n)-a]$$

$O$代表高斯金字塔的組數，$m$,$n$分別是影象的行和列。減去的係數$a$可以在$0-log_2min(m,n)$之間的任意值，和具體需要的金字塔的頂層影象的大小有關。

高斯模糊引數$\sigma$(尺度空間)，可由下面關係得到：

$$\sigma(o,s)=\sigma_0·2^{\frac{o+s}{S}}$$

其中$o$為所在的組，$s$為所在的層，$\sigma_0$為初始的尺度，$S$為每組的層數。

在Lowe論文中$\sigma_0=1.6$，$o_{min}=-1$，$S=3$,$o_{min}=-1$就是首先將原影象的長和寬各擴充套件一倍(為了保留原始影象資訊，增加特徵點數量)。

從上面可以得到同一組內相鄰的影象尺度關係：

$$\sigma_{s+1}=k·\sigma_s=2^{\frac{1}{S}}·\sigma_s$$

相鄰組處於同一層之間的影象尺度關係：

$$\sigma_{o+1}=2\sigma_o$$

下面是高斯尺度空間表示的一個例子：

2.3 高斯金字塔構建案例

以一張$512×512$的影象$I$為例,構建高斯金字塔步驟:(從0開始計數，倒立的金字塔)

1、金字塔的組數，$log_2{512}=9$，減去因子3，構建的金字塔組數為$O=6$，取每組的層數為$S=3$，相鄰兩個高斯尺度空間的比例因子$k=2^{\frac{1}{S}}=2^{\frac{1}{3}}$；

2、構建第0組，將影象的寬和高都增加一倍，變成$1024×1024$($I_0$)。第0層$I_0*G(x,y,\sigma_0)$，第1層$I_0*G(x,y,k\sigma_0)$，第2層$I_0*G(x,y,k^2\sigma_0)$；

3、構建第1組，對$I_0$降維取樣變成$512×512$($I_1$)。第0層$I_1*G(x,y,2\sigma_0)$，第1層$I_1*G(x,y,2k\sigma_0)$，第2層$I_1*G(x,y,2k^2\sigma_0)$；

4、......

5、構建第$o$組，第$s$層$I_o*G(x,y,2^ok^s\sigma_0)$;

高斯金字塔構建成功後，將每一組相鄰的兩層相減就可以得到DoG金字塔。

 3、DoG空間極值檢測

為了尋找DoG金字塔尺度空間的極值點，每個畫素點要和其影象域（相同大小的影象）和尺度域（相鄰的尺度空間）的所有相鄰點進行比較，當其大於（或者小於）所有相鄰點時，該點就是極值點。如圖所示，中間的檢測點要和其所在影象的$3×3$鄰域8個畫素點，以及其相鄰的上下兩層$3×3$鄰域18個畫素點，共26個畫素點進行比較。

從上面的描述中可以知道，不同組的影象大小不一樣，因此每組影象的第一層和最後一層是無法進行比較取得極值的。為了滿足尺度變換的連續性，在每一組影象繼續使用高斯模糊生成3幅影象，高斯金字塔每組$S+3$層影象,DoG金字塔的每組有$S+2$層影象.

3.1 尺度變化的連續性

設$S=3$,也就是每組有3層，則$k=2^{\frac{1}{S}}=2^{\frac{1}{3}}$。如果按照之前的計算，也就是高斯金字塔每組有3層影象，DoG金字塔每組有2層影象，在DoG金字塔的第一組有兩層尺度分別是$\sigma$,$k\sigma$,$k^2\sigma$，第二組有兩層尺度分別是$2\sigma$,$2k\sigma$,由於只有兩項是無法比較取得極值的(只有左右兩邊都有值才能有極值)，我們必須在高斯空間繼續新增高斯模糊項，使得DoG空間尺度形成$\sigma$,$k\sigma$,$k^2\sigma$,$k^3\sigma$,$k^4\sigma$，這樣就可以選擇中間的三項$k\sigma$,$k^2\sigma$,$k^3\sigma$。對應的下一組由上一組降維取樣得到的三項是$2k\sigma$,$2k^2\sigma$,$2k^3\sigma$,其首項$2k\sigma=2·2^{\frac{1}{3}}\sigma=2^{\frac{4}{3}}\sigma$，剛好與上一組的最後一項$k^3\sigma=2^{\frac{3}{3}}\sigma$尺度連線起來。所以需要在每一組影象繼續使用高斯模糊生成3幅影象，高斯金字塔每組有$S+3$層影象,DoG金字塔的每組有$S+2$層影象。

下面是區域性極值檢測的結果：

 4、刪除不好的極值點(特徵點)

到現在，我們已經得到了部分關鍵點，但是現在存在幾個問題，通過比較檢測得到的DoG的區域性極值點是在離散的空間搜尋得到的，由於離散空間是對連續空間取樣得到的結果，因此在離散空間找到的極值點不一定是真正意義上的極值點，因此要設法將不滿足條件的點剔除掉。可以通過尺度空間DoG函式進行曲線擬合尋找極值點，這一步的本質是去掉DoG局部曲率非常不對稱的點，增強匹配穩定性、提高抗噪聲能力，以達到精確定位關鍵點的目的。

利用已知的離散空間點插值得到的連續空間極值點的方法叫做子畫素插值（Sub-pixelInterpolation）。

要剔除掉的不符合要求的點主要有兩種：

• 低對比度的特徵點;
• 不穩定的邊緣響應點;

4.1 剔除低對比度的特徵點

假設我們在尺度為$\sigma$的尺度影象$D(x,y)$上檢測到了一個區域性極值點，空間位置為$(x,y,\sigma)$，為了簡單方便我們使用$x$表示這個候選點，其極值點偏移量用$Δx$表示，為了提高關鍵點的穩定性，需要對尺度空間DoG函式進行曲線擬合。利用DoG函式在尺度空間的泰勒展開式(擬合函式)為：

$$D(x+Δx)=D(x)+\frac{\partial{D^T}}{\partial{x}}Δx+\frac{1}{2}Δx^T\frac{\partial^2D}{\partial{x^2}}Δx$$

對$Δx$求導並讓方程等於零，可以得到極值點的偏移量為：

$$Δx=-\frac{\partial^2D^{-1}}{\partial{x^2}}\frac{\partial{D(x)}}{\partial{x}}$$

然後再把求得的$Δx$帶入到$D(x)$的泰勒展開式中：

$$D(\hat{x})=D(x)+\frac{1}{2}\frac{\partial{D^T}}{\partial{x}}Δx$$

其中$\hat{x}=x+Δx$,設對比度的閾值為$T$,對比度為$D(x)$的絕對值$|D(x)|$，若$|D(\hat{x})|≥T$,則該特徵點保留，否則剔除掉。

下面是刪除$D(x)$絕對值較小後的結果：

 4.2 剔除不穩定的邊緣響應點

有些極值點的位置是在影象的邊緣位置的，因為影象的邊緣點很難定位，同時也容易受到噪聲的干擾，我們把這些點看做是不穩定的極值點，需要進行去除。

在邊緣梯度的方向上主曲率值比較大，而沿著邊緣方向則主曲率值較小。候選特徵點的DoG函式$D(x)$的主曲率與$2×2$Hessian矩陣$H$的特徵值成正比：

$$H=\begin{bmatrix}D_{xx} & D_{yx} \\ D_{xy} & D_{yy} \end{bmatrix}$$

其中,$D_{xx}$,$D_{xy}$,$D_{yy}$是候選點鄰域位置差分求得的。

為了避免求具體的值，可以使用$H$特徵值的比例.設$\alpha=\lambda_{max}$為$H$的最大特徵值,$\beta=\lambda_{min}$為$H$的最小特徵值,則:

$$T_r(H)=D_{xx}+D_{yy}=\alpha+\beta$$

$$Det(H)=D_{xx}+D_{yy}-D^2_{xy}=\alpha·\beta$$

其中，$T_r(H)$為矩陣$H$的跡,$Det(H)$為矩陣$H$的行列式.

設$\gamma=\frac{\alpha}{\beta}$表示最大特徵值與最小特徵值的比值，則：

$$\frac{T_r(H)^2}{Det(H)}=\frac{(\alpha+\beta)^2}{\alpha\beta}=\frac{(\gamma\beta+\beta)^2}{\gamma\beta^2}=\frac{(\gamma+1)^2}{\gamma}$$
上式的結果與兩個特徵值的比例有關，和具體的大小無關，當兩個特徵值相等時其值最小，並且隨著$\gamma$的增大而增大。因此為了檢測主曲率是否在某個閾值$T_r$下，只需檢測：

$$\frac{T_r(H)^2}{Det(H)}>\frac{(T_{\gamma}+1)^2}{T_{\gamma}}$$

如果上式成立，則剔除該特徵點，否則保留。（Lowe論文中取$T_{\gamma}=10$)

我們知道邊緣$H$矩陣一個特徵值很大,一個特徵值很小,因此可以通過過濾較大的$\gamma$值達到過濾邊緣的目的。具體可參見Harris角點檢測演算法第十一節、Harris角點檢測原理。

下面是移除邊緣響應後的結果：

5、求取特徵點的主方向

經過上面的步驟已經找到了在不同尺度下都存在的特徵點，為了實現影象旋轉不變性，需要給特徵點的方向進行賦值。利用特徵點鄰域畫素的梯度來確定其方向引數，再利用影象的梯度直方圖求取關鍵點區域性結構的穩定方向。
對於已經檢測到的特徵點，我們知道該特徵點的尺度值$\sigma$，因此根據這一尺度值，也就可以得到這一尺度的高斯影象：

$$L(x,y)=G(x,y,\sigma)*I(x,y)$$

使用有限差分，計算以特徵點為中心，$3×1.5\sigma$為半徑的區域影象的幅角和幅值，每個點$L(x,y)$的梯度的模$m(x,y)$以及方向$\theta(x,y)$可通過下面公式得到：

$$m(x,y)=\sqrt{[L(x+1,y)-L(x-1,y)]^2+[L(x,y+1)-L(x,y-1)]^2}$$

$$\theta(x,y)=arctan\frac{L(x,y+1)-L(x,y-1)}{L(x+1,y)-L(x-1,y)}$$

計算得到梯度方向後，就要使用直方圖統計特徵點鄰域內畫素對應的梯度方向和幅值。梯度方向的直方圖的橫軸是梯度方向的角度（梯度方向的範圍是0到360度，直方圖每36度一個柱共10個柱，或者每45度一個柱共8個柱），縱軸是梯度方向對應梯度幅值的累加，在直方圖的峰值就是特徵點的主方向。

在Lowe的論文還提到了使用高斯函式對直方圖進行平滑以增強特徵點近的鄰域點對關鍵點方向的作用，並減少突變的影響。為了得到更精確的方向，通常還可以對離散的梯度直方圖進行插值擬合。具體而言，關鍵點的方向可以由和主峰值最近的三個柱值通過拋物線插值得到。在梯度直方圖中，當存在一個相當於主峰值80%能量的柱值時，則可以將這個方向認為是該特徵點輔助方向。所以，一個特徵點可能檢測到多個方向（也可以理解為，一個特徵點可能產生多個座標、尺度相同，但是方向不同的特徵點）。Lowe在論文中指出15%的關鍵點具有多方向，而且這些點對匹配的穩定性很關鍵。

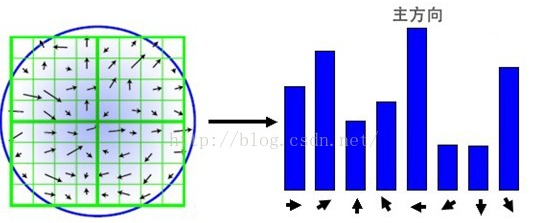
得到特徵點的主方向後，對於每個特徵點可以得到三個資訊$(x,y,\sigma,\theta)$,即位置、尺度和方向。由此可以確定一個SIFT特徵區域，一個SIFT特徵區域由三個值表示，中心表示特徵點位置，半徑表示關鍵點的尺度，箭頭表示主方向。具有多個方向的關鍵點可以被複製成多份，然後將方向值分別賦給複製後的特徵點，一個特徵點就產生了多個座標、尺度相等，但是方向不同的特徵點。

下面是特徵方向和尺度分配的結果（箭頭指向代表方向，長度代表尺度）：

6、生成特徵描述

通過以上的步驟已經找到了SIFT特徵點位置、尺度和方向資訊，下面就需要使用一組向量來描述關鍵點也就是生成特徵點描述子，這個描述符不只包含特徵點，也含有特徵點周圍對其有貢獻的畫素點。描述子應具有較高的獨立性，以保證匹配率。
特徵描述符的生成大致有三個步驟：

• 校正旋轉主方向，確保旋轉不變性。
• 生成描述子，最終形成一個128維的特徵向量
• 歸一化處理，將特徵向量長度進行歸一化處理，進一步去除光照的影響。

為了保證特徵向量的旋轉不變性，要以特徵點為中心，在附近鄰域內將座標軸旋轉$\theta$（特徵點的主方向）角度，即將座標軸旋轉為特徵點的主方向。

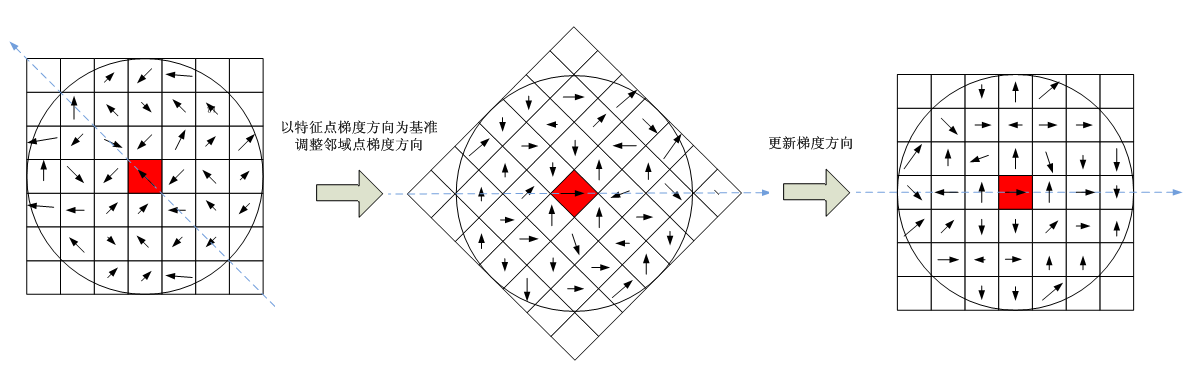
到這裡，有人會問：旋轉過程中，中圖和右圖為什麼每個畫素點的方向不一樣？其實，你要明確一點，你所選的小區域，是關鍵點旋轉後的小區域，右圖的區域跟旋轉前的區域不一樣了，右圖是重新選取得區域，但是區域大小沒變。

旋轉後鄰域內畫素的新座標為：

$$\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} cos\theta & –sin\theta \\ sin\theta & cos\theta \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}$$

旋轉後以主方向為中心取$3\sigma{d}\times3\sigma{d}$(下圖中$d=4$)的視窗。下圖所示，左圖的中央為當前關鍵點的位置，每個小格代表為關鍵點鄰域所在尺度空間的一個畫素，求取每個畫素的梯度幅值與梯度方向，箭頭方向代表該畫素的梯度方向，長度代表梯度幅值，然後利用高斯視窗對其進行加權運算。最後在每個$3\sigma\times3\sigma$的小塊上(影象中每個正方形的區域的邊長為$4$)繪製8個方向的梯度直方圖，計算每個梯度方向的累加值，即可形成一個種子點，如右圖所示。每個特徵點由4個種子點組成，每個種子點有8個方向的向量資訊。這種鄰域方向性資訊聯合增強了演算法的抗噪聲能力，同時對於含有定位誤差的特徵匹配也提供了比較理性的容錯性。

注意：由於實際情況下，程式設計時用到雙線性差值(前面用到了旋轉，旋轉操作會用到插值處理)，因此這裡用到的特徵點鄰域的邊長實際為$3\sigma{(d+1)}$。因此鄰域中一共有$(3\sigma{(d+1)})^2$個畫素點。

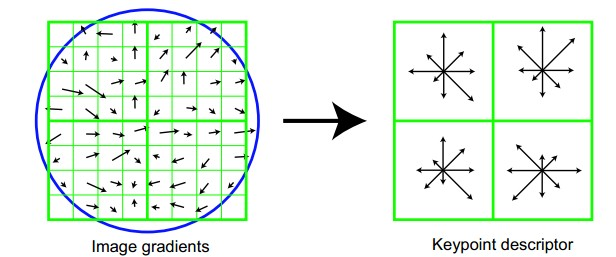
與求主方向不同，此時每個種子區域的梯度直方圖在0-360之間劃分為8個方向區間，每個區間為45度，即每個種子點有8個方向的梯度強度資訊。
在實際的計算過程中，為了增強匹配的穩健性，Lowe建議對每個關鍵點使用$4\times4$共16個種子點來描述，這樣一個關鍵點就可以產生128維的SIFT特徵向量。

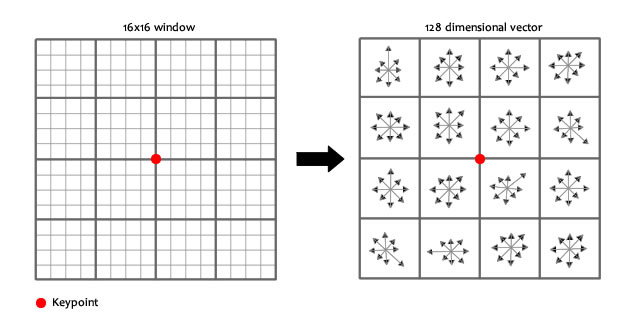
通過對特徵點周圍的畫素進行分塊，計算塊內梯度直方圖，生成具有獨特性的向量，這個向量是該區域影象資訊的一種抽象，具有唯一性。

上面講了那麼多，我們來總結一下特徵點鄰域每個畫素點對於整個梯度直方圖的貢獻的計算如下所述：

1. 計算各個畫素點的梯度幅值和梯度幅角；
2. 根據該畫素點距離特徵點的距離進行加權（即第一次高斯加權），該畫素點的幅值乘以加權值；
3. 根據該畫素點在所在的小正方形區域內據中心的距離進行加權（即第二次高斯加權），把2中的結果再乘以一個權值。

經過上面的計算，就可以得到128柱的直方圖$\{p_1,p_2,...,p_{128}\}$，為了去除光照的影響，需要進行歸一化處理：

$$q_i=\frac{p_i}{\sqrt{p_1^2+p_2^2+...+p_{128}^2}},i=1,2,3,...,128$$

實際上為了去除非線性光照的變化，在實現的過程中對於已經歸一化好的描述符$\{q_1,q_2,...,q_{128}\}$需要設定一個閾值，一般閾值為0.2，當$q_i$超過0.2以後，則$q_i=0.2$。

7、總結

SIFT特徵以其對旋轉、尺度縮放、亮度等保持不變性，是一種非常穩定的區域性特徵，在影象處理和計算機視覺領域有著很重要的作用，其本身也是非常複雜的，下面對其計算過程做一個粗略總結。

1、DoG尺度空間的極值檢測。 首先是構造DoG尺度空間，在SIFT中使用不同引數的高斯模糊來表示不同的尺度空間。而構造尺度空間是為了檢測在不同尺度下都存在的特徵點，特徵點的檢測比較常用的方法$\sigma^2\nabla^2G$（高斯拉普拉斯LoG），但是LoG的運算量是比較大的，Marr和Hidreth曾指出，可以使用DoG（差分高斯）來近似計算LoG，所以在DoG的尺度空間下檢測極值點。

2、刪除不穩定的極值點。主要刪除兩類：低對比度的極值點以及不穩定的邊緣響應點。

3、確定特徵點的主方向。以特徵點的為中心、以$3×1.5\sigma$為半徑的領域內計算各個畫素點的梯度的幅角和幅值，然後使用直方圖對梯度的幅角進行統計。直方圖的橫軸是梯度的方向，縱軸為梯度方向對應梯度幅值的累加值，直方圖中最高峰所對應的方向即為特徵點的方向。

4、生成特徵點的描述子。 首先將座標軸旋轉為特徵點的方向，以特徵點為中心的$16\times16$視窗的畫素的梯度幅值和方向，將視窗內的畫素分成16塊，每塊是其畫素內8個方向的直方圖統計，共可形成128維的特徵向量。

三 特徵點匹配

既然是匹配，當然每個特徵點的特徵向量(描述符)要相似才能匹配到一起，這裡採用的是歐式距離來衡量其相似度。比如說我有2張圖片A和B，圖片的內容相同，只是圖片的大小尺寸不同。假設A圖片尺寸比較大，且我們已經採用SIFT演算法對圖片A和B都進行了特徵提取，獲得了它們的特徵點集合，現在我們的問題是需要把A和B中相應的特徵點給對應連線起來。

對B中的特徵點x，去尋找A中最相似的點y，最簡單的方法就是拿x與A中所有點進行相似度比較，距離最小的那個為匹配點。但是如果圖片中特徵點數目很多的話，這樣效率會很低。所以我們需要把A中特徵點向量集合用一種資料結構來描述，這種描述要有利於x在A中的搜尋，即減少時間複雜度。在sift匹配中，這種資料結構採用的是kd-tree。關於kd-tree的講解，可以參考博文k-d tree演算法的研究.

# -*- coding: utf-8 -*-
"""
Created on Wed Aug 22 16:53:16 2018

@author: lenovo
"""

'''
SIFT演算法
'''
import cv2

'''1、載入圖片'''
img1 = cv2.imread('./image/match1.jpg')
img1 = cv2.resize(img1,dsize=(600,400))
gray1 = cv2.cvtColor(img1,cv2.COLOR_BGR2GRAY)
img2 = cv2.imread('./image/match2.jpg')
img2 = cv2.resize(img2,dsize=(600,400))
gray2 = cv2.cvtColor(img2,cv2.COLOR_BGR2GRAY)
image1 = gray1.copy()
image2 = gray2.copy()

'''2、提取特徵點'''
#建立一個SIFT物件
sift = cv2.xfeatures2d.SIFT_create(400)
#SIFT物件會使用DoG檢測關鍵點，並且對每個關鍵點周圍的區域計算特徵向量。該函式返回關鍵點的資訊和描述符
keypoints1,descriptor1 = sift.detectAndCompute(image1,None)
keypoints2,descriptor2 = sift.detectAndCompute(image2,None)
print('descriptor1:',descriptor1.shape,'descriptor2',descriptor2.shape)
#在影象上繪製關鍵點
image1 = cv2.drawKeypoints(image=image1,keypoints = keypoints1,outImage=image1,color=(255,0,255),flags=cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)
image2 = cv2.drawKeypoints(image=image2,keypoints = keypoints2,outImage=image2,color=(255,0,255),flags=cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)
#顯示影象
cv2.imshow('sift_keypoints1',image1)
cv2.imshow('sift_keypoints2',image2)
cv2.waitKey(20)


'''3、特徵點匹配'''
matcher = cv2.FlannBasedMatcher()
matchePoints = matcher.match(descriptor1,descriptor2)
print(type(matchePoints),len(matchePoints),matchePoints[0])

#提取強匹配特徵點
minMatch = 1
maxMatch = 0
for i in range(len(matchePoints)):
    if  minMatch > matchePoints[i].distance:
        minMatch = matchePoints[i].distance
    if  maxMatch < matchePoints[i].distance:
        maxMatch = matchePoints[i].distance
print('最佳匹配值是:',minMatch)        
print('最差匹配值是:',maxMatch)      

#獲取排雷在前邊的幾個最優匹配結果
goodMatchePoints = []
for i in range(len(matchePoints)):
    if matchePoints[i].distance < minMatch + (maxMatch-minMatch)/3:
        goodMatchePoints.append(matchePoints[i])

#繪製最優匹配點
outImg = None
outImg = cv2.drawMatches(img1,keypoints1,img2,keypoints2,goodMatchePoints,outImg,matchColor=(0,255,0),flags=cv2.DRAW_MATCHES_FLAGS_DEFAULT)
cv2.imshow('matche',outImg)
cv2.waitKey(0)
cv2.destroyAllWindows()

我們選擇的這兩幅圖片亮度和對比度差異都是很大的，而且拍攝所使用的相機也是不同的，拍攝出來的同一物體尺寸也是不用的，左側是我自己用手機拍攝到的，右側是從網上下載的，可以看到匹配效果還不錯。這也說明了SIFT演算法的優越性：對旋轉、尺度縮放、亮度變化等保持不變性，對視角變換、仿射變化、噪聲也保持一定程度的穩定性。但是如果我們想達到更高的匹配度，我們應該儘量選擇兩張更為相似的圖片。

參考文章：