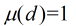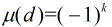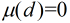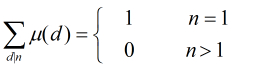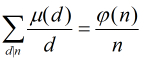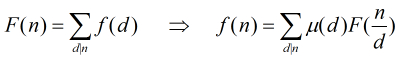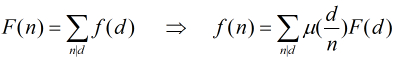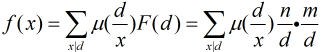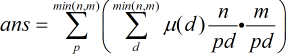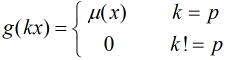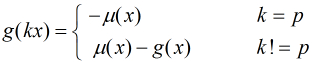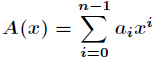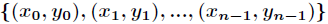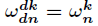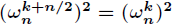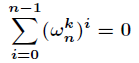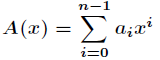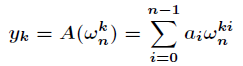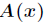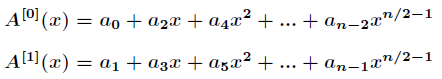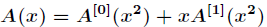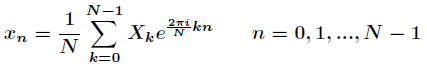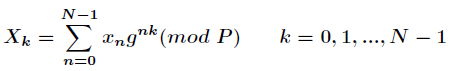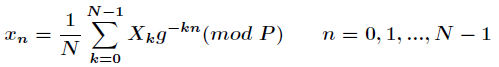莫比烏斯反演在數論中佔有重要的地位，許多情況下能大大簡化運算。那麼我們先來認識莫比烏斯反演公式。

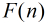
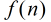
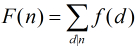
定理：和是定義在非負整數集合上的兩個函式，並且滿足條件，那麼我們得到結論

在上面的公式中有一個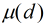函式，它的定義如下：

    （1）若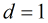，那麼

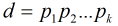
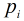
    （2）若，均為互異素數，那麼

    （3）其它情況下

對於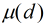函式，它有如下的常見性質：

    （1）對任意正整數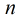有

        （2）對任意正整數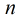有

線性篩選求莫比烏斯反演函式程式碼。

void Init()
{
    memset(vis,0,sizeof(vis));
    mu[1] = 1;
    cnt = 0;
    for(int i=2; i<N; i++)
    {
        if(!vis[i])
        {
            prime[cnt++] = i;
            mu[i] = -1;
        }
        for(int j=0; j<cnt&&i*prime[j]<N; j++)
        {
            vis[i*prime[j]] = 1;
            if(i%prime[j]) mu[i*prime[j]] = -mu[i];
            else
            {
                mu[i*prime[j]] = 0;
                break;
            }
        }
    }
}
 

有了上面的知識，現在我們來證明莫比烏斯反演定理。

證明

證明完畢！

嗯，有了莫比烏斯反演，很多問題都可以簡化了，接下來我們來看看莫比烏斯反演在數論中如何簡化運算的。

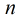
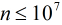
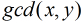
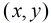
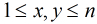
題意：給一個正整數，其中，求使得為質數的的個數，。

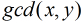
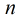
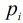
分析：對於本題，因為是使得為質數，所以必然要列舉小於等於的質數，那麼對於每一個質數，只

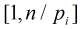
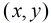
     需要求在區間中，滿足有序對互質的對數。

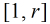
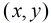
     也就是說，現在問題轉化為：在區間中，存在多少個有序對使得互質，這個問題就簡單啦，因為

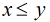
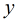
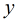
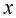
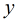
     是有序對，不妨設，那麼我們如果列舉每一個，小於有多少個與互素，這正是尤拉函式。所以

     我們可以遞推法求尤拉函式，將得到的答案乘以2即可，但是這裡乘以2後還有漏計算了的，那麼有哪些呢？

     是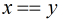且為素數的情況，再加上就行了。

程式碼：

#include <iostream>
#include <string.h>
#include <stdio.h>
#include <bitset>

using namespace std;
typedef long long LL;
const int N = 10000010;

bitset<N> prime;
LL phi[N];
LL f[N];
int p[N];
int k;

void isprime()
{
    k = 0;
    prime.set();
    for(int i=2; i<N; i++)
    {
        if(prime[i])
        {
            p[k++] = i;
            for(int j=i+i; j<N; j+=i)
                prime[j] = false;
        }
    }
}

void Init()
{
    for(int i=1; i<N; i++)  phi[i] = i;
    for(int i=2; i<N; i+=2) phi[i] >>= 1;
    for(int i=3; i<N; i+=2)
    {
        if(phi[i] == i)
        {
            for(int j=i; j<N; j+=i)
                phi[j] = phi[j] - phi[j] / i;
        }
    }
    f[1] = 0;
    for(int i=2;i<N;i++)
        f[i] = f[i-1] + (phi[i]<<1);
}

LL Solve(int n)
{
    LL ans = 0;
    for(int i=0; i<k&&p[i]<=n; i++)
        ans += 1 + f[n/p[i]];
    return ans;
}

int main()
{
    Init();
    isprime();
    int n;
    scanf("%d",&n);
    printf("%I64d\n",Solve(n));
    return 0;
}
 

上題不算太難，普通的尤拉函式就可以搞定，接下來我們來看看它的升級版。

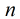
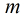
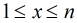
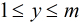
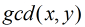
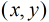
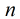
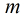
題意：給定兩個數和，其中，，求為質數的有多少對？其中和的範

     圍是。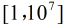

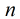
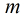
分析：本題與上題不同的是和不一定相同。在這裡我們用莫比烏斯反演來解決，文章開頭也說了它能大大簡化

     運算。我們知道莫比烏斯反演的一般描述為：

     其實它還有另一種描述，本題也是用到這種。那就是：

     好了，到了這裡，我們開始進入正題。。。

     對於本題，我們設

     為滿足且和的的對數

     為滿足且和的的對數

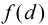
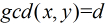
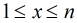
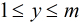
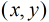
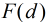
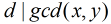
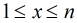
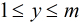
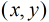
     那麼，很顯然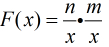，反演後得到

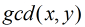
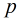
     因為題目要求是為質數，那麼我們列舉每一個質數，然後得到

     如果直接這樣做肯定TLE，那麼我們必須優化。

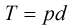
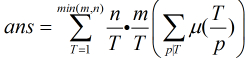
     我們設，那麼繼續得到。

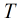
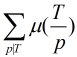
     到了這裡，可以看出如果我們可以先預處理出所有的對應的的值，那麼本題就解決了。

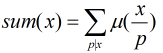
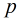
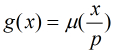
     我們設，注意這裡為素數，。

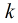
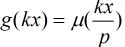
     那麼，我們列舉每一個，得到，現在分情況討論：

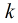
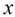
     （1）如果整除，那麼得到

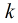
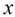
     （2）如果不整除，那麼得到

程式碼：

#include <iostream>
#include <string.h>
#include <stdio.h>

using namespace std;
typedef long long LL;
const int N = 10000005;

bool vis[N];
int p[N];
int cnt;
int g[N],u[N],sum[N];

void Init()
{
    memset(vis,0,sizeof(vis));
    u[1] = 1;
    cnt = 0;
    for(int i=2;i<N;i++)
    {
        if(!vis[i])
        {
            p[cnt++] = i;
            u[i] = -1;
            g[i] = 1;
        }
        for(int j=0;j<cnt&&i*p[j]<N;j++)
        {
            vis[i*p[j]] = 1;
            if(i%p[j])
            {
                u[i*p[j]] = -u[i];
                g[i*p[j]] = u[i] - g[i];
            }
            else
            {
                u[i*p[j]] = 0;
                g[i*p[j]] = u[i];
                break;
            }
        }
    }
    sum[0] = 0;
    for(int i=1;i<N;i++)
        sum[i] = sum[i-1] + g[i];
}

int main()
{
    Init();
    int T;
    scanf("%d",&T);
    while(T--)
    {
        LL n,m;
        cin>>n>>m;
        if(n > m) swap(n,m);
        LL ans = 0;
        for(int i=1,last;i<=n;i=last+1)
        {
            last = min(n/(n/i),m/(m/i));
            ans += (n/i)*(m/i)*(sum[last]-sum[i-1]);
        }
        cout<<ans<<endl;
    }
    return 0;
}

多項式乘法運算初級版——快速傅立葉變換

快速傅立葉變換在資訊學競賽中主要用於求卷積，或者說多項式乘法。我們知道，多項式乘法的普通演算法時間複雜度

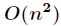
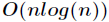
是，通過快速傅立葉變換可以使時間降為，那麼接下來會詳細介紹快速傅立葉變換的原理。

首先來介紹多項式的兩種表示方法，即係數表示法和點值表示法。從某種意義上說，這兩種方法是等價的。先設

（1）係數表示法

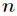
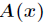
    對於一個次數界為的多項式來說，其係數表示法就是一個由係數組成的向量，很

    明顯，這樣的多項式乘法運算的時間複雜度為。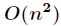

（2）點值表示法

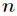
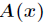
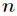
    對於一個次數界為的多項式來說，其點值是個點值對所形成的集合

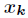
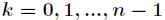
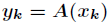
    其中各不相同，並且當時，有。可以看出一個多項式可以有多種不同的點值

    表示法，而通過這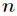個不同的點值對可以表示一個唯一的多項式。而通過點值表示法來計算多項式的乘法，時間

    複雜度為。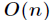

    從原則上來說，計算多項式的點值是簡單易行的，因為我們只需要先選取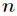個相異的點，然後通過秦九韶演算法可

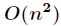
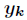
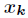
    以在時間內求出所有的，實際上如果我們的選得巧妙的話，就可以加速這一過程，使其執行時間變

    為。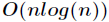

    根據多項式的係數表示法求其點值表示法的過程稱為求值，而根據點值表示法求其係數表示法的過程稱為插值。

    對於求卷積或者說多項式乘法運算問題，先是通過傅立葉變換對係數表示法的多項式進行求值運算，這一步的時

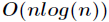
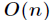
    間複雜度為，然後在時間內進行點值相乘，再進行插值運算。

那麼，接下來就是我們今天的重點了，如何高效地對一個多項式進行求值運算，即將多項式的表示法變為點值表示法。

如果選取單位復根作為求值點，則可以通過對係數向量進行離散傅立葉變換（DFT），得到相應的點值表示。同樣地

也可以通過對點值對進行逆DFT運算，獲得相應的係數向量。DFT和逆DFT的時間複雜度均為。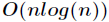

一. 求DFT

    選取次單位復根作為來求點值是比較巧妙的做法。

    次單位復根是滿足的複數，次單位復根恰好有個，它們是，，為

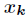
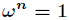
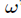
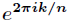
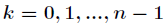
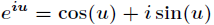
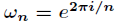
    瞭解釋這一式子，利用複數冪的定義，值稱為主次單位根，所有其

    它次單位復根都是的次冪。

    個次單位復根在乘法運算下形成一個群，該群的結構與加法群模相同。

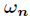
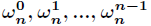
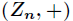
    接下來認識幾個關於次單位復根的重要性質。

    （1）相消引理

        對於任何整數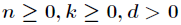，有

    （2）折半引理

        如果且為偶數，則

    （3）求和引理

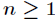
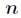
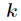
        對任意整數和不能被整除的非零整數，有

     回顧一下，我們希望計算次數界為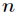的多項式

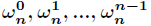
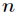
     在處的值，假定是2的冪，因為給定的次數界總可以增大，如果需要，總可以新增值為零

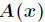
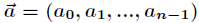
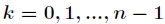
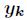
     的新的高階係數。假定已知的係數形式為，對，定義結果

     如下

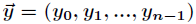
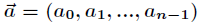
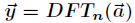
     向量是係數向量的離散傅立葉變換，寫作。

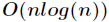
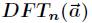
     通過使用一種稱為快速傅立葉變換（FFT）的方法，就可以在時間內計算出，而直接

     計算的方法所需時間為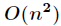，FFT主要是利用單位復根的特殊性質。FFT方法運用了分治策略，它用

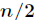
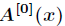
     中偶數下標的係數與奇數下標的係數，分別定義了兩個新的次數界為的多項式和

     則進一步有

     這樣在處的值得問題就轉換為求次數界為的多項式和在點

     處的值。由於在奇偶分類時導致順序發生變化，所以需要先通過Rader演算法進行

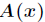
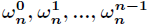
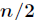
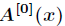
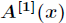
     倒位序，在FFT中最重要的一個操作是蝴蝶操作，通過蝴蝶操作可以將前半部分和後半部分的值求出。

題意：大數乘法，需要用FFT實現。

程式碼：

#include <iostream>
#include <string.h>
#include <stdio.h>
#include <math.h>

using namespace std;
const int N = 500005;
const double PI = acos(-1.0);

struct Virt
{
    double r, i;

    Virt(double r = 0.0,double i = 0.0)
    {
        this->r = r;
        this->i = i;
    }

    Virt operator + (const Virt &x)
    {
        return Virt(r + x.r, i + x.i);
    }

    Virt operator - (const Virt &x)
    {
        return Virt(r - x.r, i - x.i);
    }

    Virt operator * (const Virt &x)
    {
        return Virt(r * x.r - i * x.i, i * x.r + r * x.i);
    }
};

//雷德演算法--倒位序
void Rader(Virt F[], int len)
{
    int j = len >> 1;
    for(int i=1; i<len-1; i++)
    {
        if(i < j) swap(F[i], F[j]);
        int k = len >> 1;
        while(j >= k)
        {
            j -= k;
            k >>= 1;
        }
        if(j < k) j += k;
    }
}

//FFT實現
void FFT(Virt F[], int len, int on)
{
    Rader(F, len);
    for(int h=2; h<=len; h<<=1) //分治後計算長度為h的DFT
    {
        Virt wn(cos(-on*2*PI/h), sin(-on*2*PI/h));  //單位復根e^(2*PI/m)用尤拉公式展開
        for(int j=0; j<len; j+=h)
        {
            Virt w(1,0);            //旋轉因子
            for(int k=j; k<j+h/2; k++)
            {
                Virt u = F[k];
                Virt t = w * F[k + h / 2];
                F[k] = u + t;     //蝴蝶合併操作
                F[k + h / 2] = u - t;
                w = w * wn;      //更新旋轉因子
            }
        }
    }
    if(on == -1)
        for(int i=0; i<len; i++)
            F[i].r /= len;
}

//求卷積
void Conv(Virt a[],Virt b[],int len)
{
    FFT(a,len,1);
    FFT(b,len,1);
    for(int i=0; i<len; i++)
        a[i] = a[i]*b[i];
    FFT(a,len,-1);
}

char str1[N],str2[N];
Virt va[N],vb[N];
int result[N];
int len;

void Init(char str1[],char str2[])
{
    int len1 = strlen(str1);
    int len2 = strlen(str2);
    len = 1;
    while(len < 2*len1 || len < 2*len2) len <<= 1;

    int i;
    for(i=0; i<len1; i++)
    {
        va[i].r = str1[len1-i-1] - '0';
        va[i].i = 0.0;
    }
    while(i < len)
    {
        va[i].r = va[i].i = 0.0;
        i++;
    }
    for(i=0; i<len2; i++)
    {
        vb[i].r = str2[len2-i-1] - '0';
        vb[i].i = 0.0;
    }
    while(i < len)
    {
        vb[i].r = vb[i].i = 0.0;
        i++;
    }
}

void Work()
{
    Conv(va,vb,len);
    for(int i=0; i<len; i++)
        result[i] = va[i].r+0.5;
}

void Export()
{
    for(int i=0; i<len; i++)
    {
        result[i+1] += result[i]/10;
        result[i] %= 10;
    }
    int high = 0;
    for(int i=len-1; i>=0; i--)
    {
        if(result[i])
        {
            high = i;
            break;
        }
    }
    for(int i=high; i>=0; i--)
        printf("%d",result[i]);
    puts("");
}

int main()
{
    while(~scanf("%s%s",str1,str2))
    {
        Init(str1,str2);
        Work();
        Export();
    }
    return 0;
}

題意：給定n條長度已知的邊，求能組成多少個三角形。

分析：用一個num陣列來記錄次數，比如num[i]表示長度為i的邊有num[i]條。然後對num[]求卷積，除去本身重

     復的和對稱的，然後再整理一下就好了。

程式碼：

#include <iostream>
#include <string.h>
#include <algorithm>
#include <stdio.h>
#include <math.h>

using namespace std;
typedef long long LL;

const int N = 400005;
const double PI = acos(-1.0);

struct Virt
{
    double r,i;

    Virt(double r = 0.0,double i = 0.0)
    {
        this->r = r;
        this->i = i;
    }

    Virt operator + (const Virt &x)
    {
        return Virt(r+x.r,i+x.i);
    }

    Virt operator - (const Virt &x)
    {
        return Virt(r-x.r,i-x.i);
    }

    Virt operator * (const Virt &x)
    {
        return Virt(r*x.r-i*x.i,i*x.r+r*x.i);
    }
};

//雷德演算法--倒位序
void Rader(Virt F[],int len)
{
    int j = len >> 1;
    for(int i=1; i<len-1; i++)
    {
        if(i < j) swap(F[i], F[j]);
        int k = len >> 1;
        while(j >= k)
        {
            j -= k;
            k >>= 1;
        }
        if(j < k) j += k;
    }
}

//FFT實現
void FFT(Virt F[],int len,int on)
{
    Rader(F,len);
    for(int h=2; h<=len; h<<=1) //分治後計算長度為h的DFT
    {
        Virt wn(cos(-on*2*PI/h),sin(-on*2*PI/h));  //單位復根e^(2*PI/m)用尤拉公式展開
        for(int j=0; j<len; j+=h)
        {
            Virt w(1,0);            //旋轉因子
            for(int k=j; k<j+h/2; k++)
            {
                Virt u = F[k];
                Virt t = w*F[k+h/2];
                F[k] = u+t;      //蝴蝶合併操作
                F[k+h/2] = u-t;
                w = w*wn;      //更新旋轉因子
            }
        }
    }
    if(on == -1)
        for(int i=0; i<len; i++)
            F[i].r /= len;
}

//求卷積
void Conv(Virt F[],int len)
{
    FFT(F,len,1);
    for(int i=0; i<len; i++)
        F[i] = F[i]*F[i];
    FFT(F,len,-1);
}

int a[N];
Virt F[N];
LL num[N],sum[N];
int len,n;

void Init()
{
    memset(num,0,sizeof(num));
    scanf("%d",&n);
    for(int i=0; i<n; i++)
    {
        scanf("%d",&a[i]);
        num[a[i]]++;
    }
    sort(a, a + n);
    int len1 = a[n-1] + 1;
    len  = 1;
    while(len < len1*2) len <<= 1;
    for(int i=0; i<len1; i++)
        F[i] = Virt(num[i],0);
    for(int i=len1; i<len; i++)
        F[i] = Virt(0,0);
}

void Work()
{
    Conv(F,len);
    for(int i=0; i<len; i++)
        num[i] = (LL)(F[i].r+0.5);
    len = a[n-1]*2;
    for(int i=0; i<n; i++)
        num[a[i]+a[i]]--;
    for(int i=1; i<=len; i++)
        num[i] >>= 1;
    sum[0] = 0;
    for(int i=1; i<=len; i++)
        sum[i] = sum[i-1] + num[i];
    LL cnt = 0;
    for(int i=0; i<n; i++)
    {
        cnt+=sum[len]-sum[a[i]];
        //減掉一個取大，一個取小的
        cnt-=(LL)(n-1-i)*i;
        //減掉一個取本身，另外一個取其它
        cnt-=(n-1);
        //減掉大於它的取兩個的組合
        cnt-=(LL)(n-1-i)*(n-i-2)/2;
    }
    LL tot = (LL)n*(n-1)*(n-2)/6;
    printf("%.7lf\n",(double)cnt/tot);
}

int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        Init();
        Work();
    }
    return 0;
}

多項式乘法運算終極版——NTT（快速數論變換）

換來求多項式的乘法。可以發現它是利用了單位復根的特殊性質，大大減少了運算，但是這種做法是對複數係數的矩陣

加以處理，每個複數係數的實部和虛部是一個正弦及餘弦函式，因此大部分系數都是浮點數，我們必須做複數及浮點數

的計算，計算量會比較大，而且浮點數的計算可能會導致誤差增大。

今天，我將來介紹另一種計算多項式乘法的演算法，叫做快速數論變換（NTT），在離散正交變換的理論中，已經證明在

複數域內，具有迴圈卷積特性的唯一變換是DFT，所以在複數域中不存在具有迴圈卷積性質的更簡單的離散正交變換。

因此提出了以數論為基礎的具有迴圈卷積性質的快速數論變換。

回憶複數向量，其離散傅立葉變換公式如下

離散傅立葉逆變換公式為

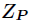
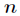
今天的快速數論變換（NTT）是在上進行的，在快速傅立葉變換（FFT）中，通過次單位復根來運算的，即滿

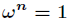
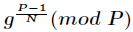
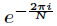
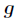
足的，而對於快速數論變換來說，則是可以將看成是的等價，這裡是模素數

的原根（由於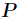是素數，那麼原根一定存在）。即

所以綜上，我們得到數論變換的公式如下

而數論變換的逆變換公式為

這樣就把複數對應到一個整數，之後一切都是在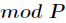系統內考慮。

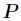
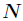
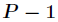
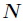
上述數論變換（NTT）公式中，要求是素數且必須是的因子。由於經常是2的方冪，所以可以構造形

如的素數。通常來說可以選擇為費馬素數，這樣的變換叫做費馬數數論變換。

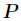
這裡我們選擇，，這樣得到模的原根值為。

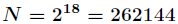
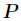
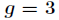
分析：題目意思就是大數相乘，此處用快速數論變換（NTT）實現。

程式碼：

#include <iostream>
#include <string.h>
#include <stdio.h>

using namespace std;
typedef long long LL;

const int N = 1 << 18;
const int P = (479 << 21) + 1;
const int G = 3;
const int NUM = 20;

LL  wn[NUM];
LL  a[N], b[N];
char A[N], B[N];

LL quick_mod(LL a, LL b, LL m)
{
    LL ans = 1;
    a %= m;
    while(b)
    {
        if(b & 1)
        {
            ans = ans * a % m;
            b--;
        }
        b >>= 1;
        a = a * a % m;
    }
    return ans;
}

void GetWn()
{
    for(int i=0; i<NUM; i++)
    {
        int t = 1 << i;
        wn[i] = quick_mod(G, (P - 1) / t, P);
    }
}

void Prepare(char A[], char B[], LL a[], LL b[], int &len)
{
    len = 1;
    int len_A = strlen(A);
    int len_B = strlen(B);
    while(len <= 2 * len_A || len <= 2 * len_B) len <<= 1;
    for(int i=0; i<len_A; i++)
        A[len - 1 - i] = A[len_A - 1 - i];
    for(int i=0; i<len - len_A; i++)
        A[i] = '0';
    for(int i=0; i<len_B; i++)
        B[len - 1 - i] = B[len_B - 1 - i];
    for(int i=0; i<len - len_B; i++)
        B[i] = '0';
    for(int i=0; i<len; i++)
        a[len - 1 - i] = A[i] - '0';
    for(int i=0; i<len; i++)
        b[len - 1 - i] = B[i] - '0';
}

void Rader(LL a[], int len)
{
    int j = len >> 1;
    for(int i=1; i<len-1; i++)
    {
        if(i < j) swap(a[i], a[j]);
        int k = len >> 1;
        while(j >= k)
        {
            j -= k;
            k >>= 1;
        }
        if(j < k) j += k;
    }
}

void NTT(LL a[], int len, int on)
{
    Rader(a, len);
    int id = 0;
    for(int h = 2; h <= len; h <<= 1)
    {
        id++;
        for(int j = 0; j < len;