AI之旅(4):初識邏輯回歸
前置知識
??求導
知識地圖

??邏輯回歸是用於分類的算法,最小的分類問題是二元分類。貓與狗,好與壞,正常與異常。掌握邏輯回歸的重點,是理解S型函數在算法中所發揮的作用,以及相關推導過程。
從一個例子開始
??假設我們是信貸工作人員,有一個關於客戶記錄的數據集。數據集中有兩個特征,x1表示月收入金額,x2表示月還貸金額。y稱為標簽,其中y=1表示客戶發生違約。

??我們的目標是挖掘出數據間可能存在的規律,建立相應的模型,用於對新客戶進行預測。假設一個新客戶的收入金額是5.0,還貸金額是2.7,請判斷客戶最可能屬於的類別。

??圖中三角形表示y=1的樣本,十字表示y=0的樣本。一般約定將關註的重點定義為y=1的類別,在這個問題中重點是尋找可能發生違約的客戶,因此將違約客戶定義為y=1。
??觀察上圖可以發現,似乎可以用一個邊界將樣本分為兩類。於是問題轉化為如何尋找到這樣的邊界,能夠將全部樣本正確地分離,或者將最多數量的樣本正確地分離。
??記得在線性回歸中,假設函數是如下形式:
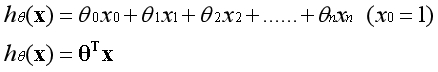
??以兩個特征為例,這既可以表現為線性模型,對應的邊界在空間中表現為一條直線:
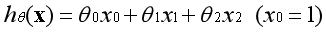
??通過添加高階多項式,也可以表現為非線性模型,對應的邊界在空間中表現為一條曲線:

??無論是線性模型還是非線性模型,從空間的角度看,模型的作用是將空間切成兩部分。從方程的角度看,模型的作用是將一個樣本映射為一個實數。用一條直線來舉例:
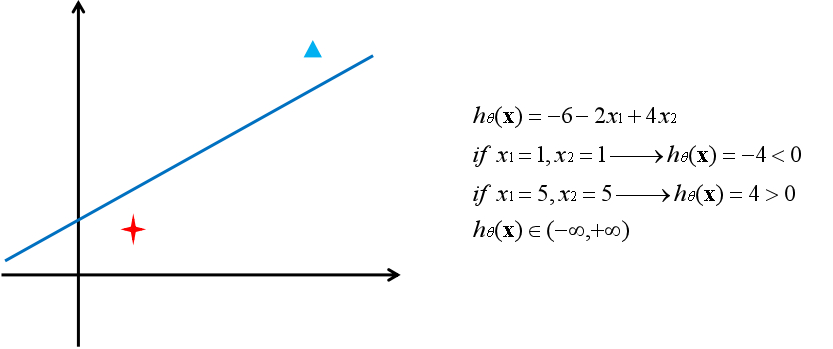
??現在的問題是這個實數的範圍屬於負無窮到正無窮,而通常是用概率的形式表示事物屬於某一類別的可能性,因此還需要一個函數將實數映射到0和1之間。
S型函數
??想象一下這個函數應該具有的形狀,當x越小時y越接近0,當x越大時y越接近1,這是一個S型的函數。S型函數有很多種,我們選擇的是名為Sigmoid的函數,也叫邏輯函數。
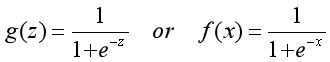
??因為特征是用x表示,為了與特征區別開,一般使用第一種形式來表示邏輯函數。函數對應的圖像如下,註意當z等於0時,Sigmoid函數的值為0.5,這是概率中的分界點。

??Sigmoid函數基本性質:
??1,定義域:(-∞,+∞);
??2,值域:(0,1);
??3,函數在定義域內為連續和光滑的曲線;
??4,處處可導,導數為:g’(z)=g(z)(1-g(z));
??Sigmoid導數推導過程:
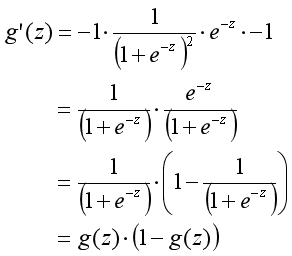
??線性回歸的模型將樣本映射為負無窮到正無窮間的實數,Sigmoid函數將該實數映射為0到1之間的數。兩者結合使用,得到的數值可以表示樣本屬於某一類別的概率。
假設函數
??邏輯回歸假設函數是在線性回歸假設函數的基礎上,再加上一個Sigmoid函數。所實現的作用是先將樣本映射為一個實數,再將實數映射為一個概率,形式如下:
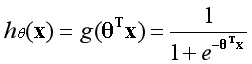
??一般表示概率是用如下形式表示,含義為在給定參數θ的情況下,當隨機變量為x時,y的概率估計。
??因為是二元分類,顯然如果一個樣本預測為y=1的概率是0.7,相應的該樣本預測為y=0的概率是0.3。在概率中以0.5作為分界點,假設函數所發揮的作用如下圖所示:
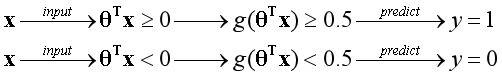
??邏輯回歸算法的最終目的,是獲得合適的參數θ,用結構圖的形式表示如下:

代價函數
??因為邏輯回歸的假設函數是非線性函數,樣本都被壓縮成0到1之間的數值,所以不適合用距離來衡量模型的準確性,我們需要構造一個新的代價函數。

??上圖是log(x)的圖像,觀察圖像的趨勢可以發現,當x接近1的時候,y接近0。當x接近0的時候,y接近負無窮。根據圖像特性可以構造第一個代價函數。
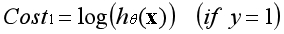
??當樣本的類別為1時,若預測樣本的類別接近1,說明預測準確,代價接近0;
??當樣本的類別為1時,若預測樣本的類別接近0,說明預測不準確,代價接近負無窮;

??上圖是log(1-x)的圖像,觀察圖像的趨勢可以發現,當x接近0的時候,y接近0。當x接近1的時候,y接近負無窮。根據圖像性質可以構造第二個代價函數。

??當樣本的類別為0時,若預測樣本的類別接近0,說明預測準確,代價接近0;
??當樣本的類別為0時,若預測樣本的類別接近1,說明預測不準確,代價接近負無窮;
??根據對數函數的圖像性質,可以構造出評估模型準確性的代價函數。當樣本類別為1時對應第一個代價函數,為0時對應第二個代價函數。能否將兩個函數合並為一個函數呢?
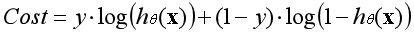
??因為y的取值只有1和0,當y等於1時函數第二部分消失,當y等於0時函數第一部分消失,這個函數包含了所有可能出現的四種情況。所以數據集的平均代價函數如下:
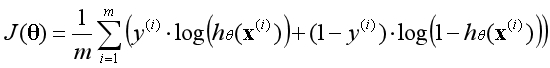
??註:這裏的log函數特指e為底的對數;
??所謂代價,是給予算法判斷錯誤的懲罰。當預測準確時,代價接近0;當預測不準確時,代價接近負無窮。因此目標是將代價函數最大化,邏輯回歸的代價函數有全局最優解。

代價函數的導數
??與線性回歸類似,邏輯回歸也是通過梯度更新的方法求最優解。首先要求出代價函數的偏導數,通過將其他變量視為常數,運用鏈式法則逐層求導,以下為推導過程:
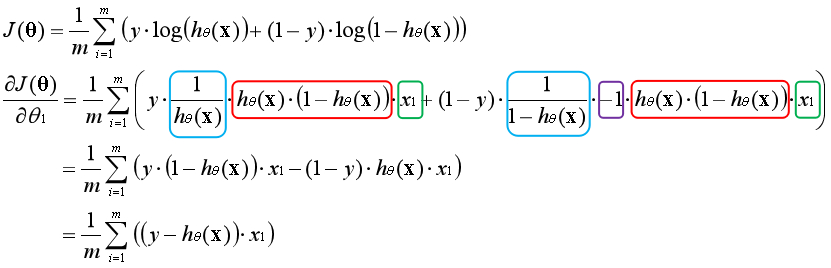
??第一層(藍色)對e為底的對數求導,第二層(紅色)對Sigmoid函數求導,第三層(綠色)對線性模型求導。
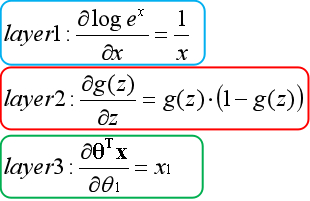
梯度上升
??梯度上升法是讓參數向偏導數的同方向調整,反復叠代,逐步靠近全局最優點的方法。從直觀上看參數從任意一個位置出發,總是一步步接近最高點的位置,如下圖所示:

??梯度上升公式(示例):
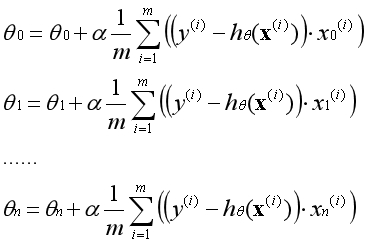
??註:α為學習率;
??註:n為特征的數量;
??在實際運用中參數θ必須同時更新,一次梯度上升指的是所有的參數運用舊的參數同時更新一次。不能先更新第一個參數,然後用更新後的第一個參數去更新第二個參數。
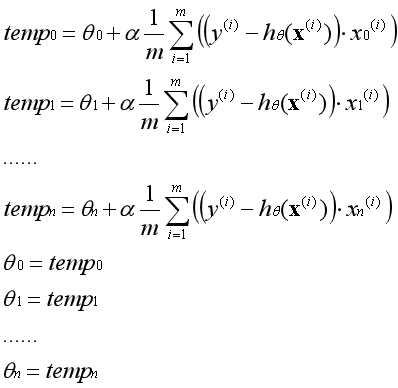
??下圖為兩個正常運行的梯度上升的代價函數圖像:

??對比線性回歸中運用的梯度下降法,可以發現這兩者本質上是同一種方法,都是通過對偏導數的反復更新逐步靠近全局最優點。
多元分類
??如果給出一個包含多個類別的數據集,如何用邏輯回歸算法對其進行分類呢?我們可以將這個問題轉化為多個獨立的二元分類問題。
??將第一類視為正項,其他項視為負項,訓練出第一個分類器;
??將第二類視為正項,其他項視為負項,訓練出第二個分類器;
??將第三類視為正項,其他項視為負項,訓練出第三個分類器;
??......
??有了多個分類器以後,將要預測的新樣本同時輸入到多個分類器中,每個分類器會給出樣本屬於該類別的概率。哪一個類別的概率最高,就預測新樣本屬於哪一類。
向量化
??如果構建一個最小單位的邏輯回歸模型,將梯度下降的方程展開後,經過適當的變換,會發現邏輯回歸的梯度上升可以用一行代碼表達。
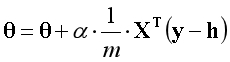
??註:X是樣本構成的矩陣,矩陣規格為(m×n);
??註:θ是參數構成的向量,向量規格為(n×1);
??註:h是假設函數,h=g(Xθ);
??註:g是Sigmoid函數;
??註:說明原理時向量的下標是從0開始,實際運用中向量的下標是從1開始;
總結
??邏輯回歸是用於分類的算法,通過線性模型將樣本映射為實數,通過Sigmoid函數將實數映射為概率,用概率衡量事物屬於某一類別的可能性。這是邏輯回歸的假設函數。
??根據對數函數的圖像性質,構造出符合要求的代價函數,這個代價函數有全局最優解。通過梯度上升的方法反復叠代,得到代表全局最優解的參數θ。這是邏輯回歸的實現方法。
??至此,我們掌握了兩個基本的算法。線性回歸可用於預測趨勢,邏輯回歸可用於判斷類別。通過對這兩個算法進行變換組合,可以構造出更強大的算法,比如神經網絡。
??回到開頭的例子,將這個小小的數據集扔到邏輯回歸算法中學習後,可以預測新客戶屬於y=1的可能性約為85%。去尋找更多的數據集來實踐吧,實踐是記憶的最好方法。
非正規代碼

版權聲明
??1,本文為原創文章,未經作者授權禁止引用、復制、轉載、摘編。
??2,對於有上述行為者,作者將保留追究其法律責任的權利。
Tieven
2019.1.7
AI之旅(4):初識邏輯回歸
