凸優化學習筆記(1)——凸集

筆記是根據《Convex Optimization》寫的，序號對應章。

2.1 凸集(convex sets)
　　如果在集合C中的任意兩點滿足：

θx1+(1−θ)x2∈C
其中0≤θ≤1，則集合C為凸集
2.2 重要例子
1) 超平面與半空間(hyperplanes and halfspaces)
　　超平面定義為{x|aTx=b}，半空間被定義為{x|aTx≤b}。從直觀上看，超平面在空間中為一塊板子，劃分的兩邊則分別為半空間。

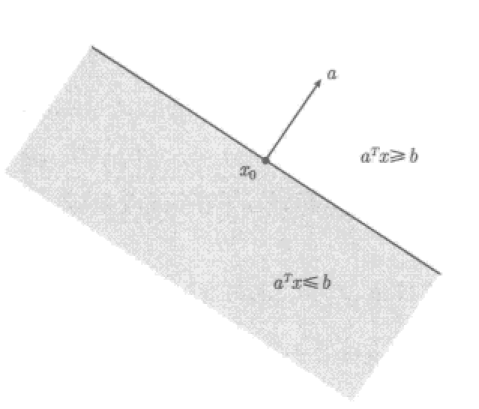
2) 球和橢球
　　球的形式為
{x|||x−xc||2≤r}={x│(x−xc)T(x−xc)≤r2}
橢球的形式為
{

x│(x−xc)TP−1(x−xc)≤1}
其中P是對稱的正定矩陣。
二維橢球

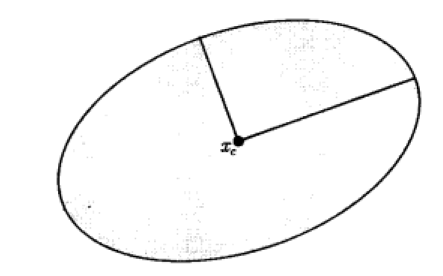
3) 範數球和範數錐
　　範數球為：
{x|||x−xc||≤r}
範數錐為：
{(x,t)|||x||≤t}

4) 多面體
{x|aTjx≤bj,j=1,…,m,cTjx≤dj,j=1,…,p}
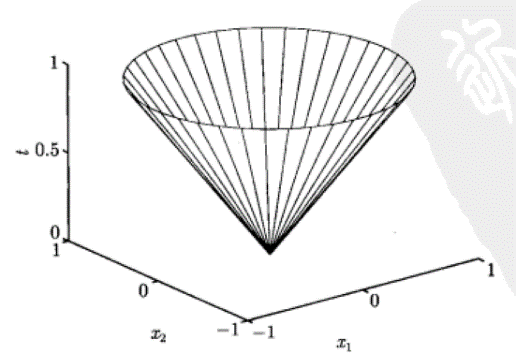
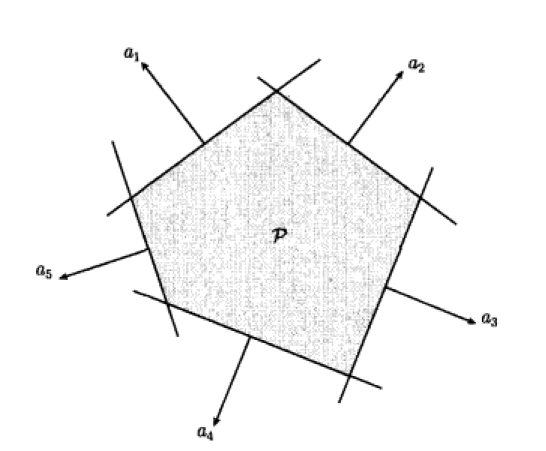
二維多面體

5) 半正定錐
　　滿足如下條件的集合Sn+是凸集：θ1、θ2≥0並且A,B∈Sn+，則θ1A+θ2B∈Sn+。其中Sn+是半正定矩陣。

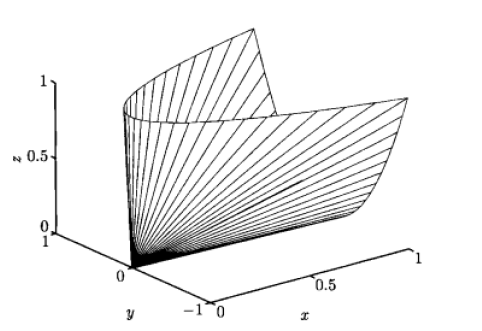
2.3 保凸運算
1) 交集
　　如果A與B均為凸集，則A與B的交集也為凸集。
2) 仿射函式
　　仿射函式即線性函式加常數。如果x為凸集，則f(x)

=Ax+b為凸集。仿射函式的逆函式也保凸。
3) 線性分式以及透視函式
　　透視函式即P(z,t)=z/t，這裡z是n−1維向量，t是最後一維分量。例如P(x1,x2,x3)={x1/x3,x2/x3}，P的定義域是正定對稱矩陣。從幾何上看，透視函式類似小孔成像，是從高維到低維的對映。

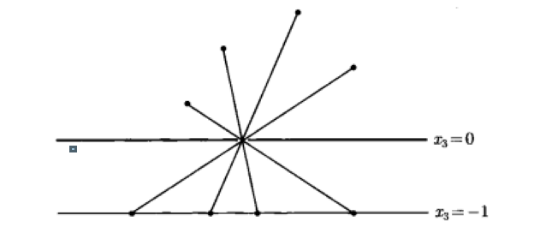
　　線性分式即f(x)=(Ax+b)/(cTx+d)其定義域為{x|cTx+d>0}。其逆函式也保凸。線性分式可看做在原集合內做拉伸，故而保凸。

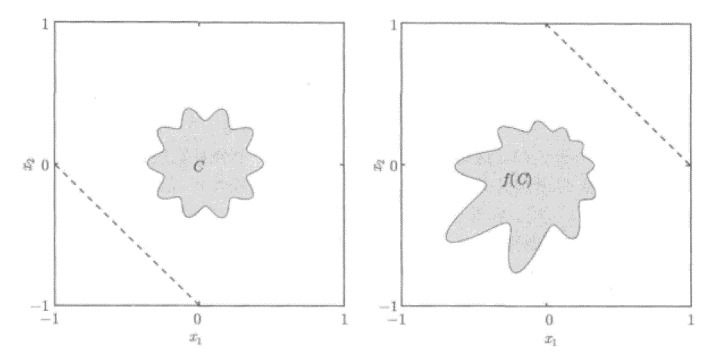
2.4 廣義不等式
　　廣義不等式即定義了擁有多個分量的變數之間的比較：
x≥ky⟺x−y∈k
x>ky⟺x−y∈int(k)
int(k)

即