前言

LSH 用於近似查詢，聚類分類，壓縮等領域。

漢明距離

漢明距離是以理查德·衛斯里·漢明的名字命名的。在資訊理論中，兩個等長字串之間的漢明距離是兩個字串對應位置的不同字元的個數。換句話說，它就是將一個字串變換成另外一個字串所需要替換的字元個數。例如：1011101 與 1001001 之間的漢明距離是 2。2143896 與 2233796 之間的漢明距離是 3。"toned" 與 "roses" 之間的漢明距離是 3。

漢明重量

漢明重量是字串相對於同樣長度的零字串的漢明距離，也就是說，它是字串中非零的元素個數：對於二進位制字串來說，就是 1 的個數，所以 11101 的漢明重量是 4。

LSH(Location Sensitive Hash),即位置敏感雜湊函式。與一般雜湊函式不同的是位置敏感性，也就是雜湊前的相似點經過雜湊之後，也能夠在一定程度上相似，並且具有一定的概率保證。

形式化定義：

對於任意q,p屬於S，若從集合S到U的函式族H={h1,h2...hn}對距離函式D(,)，如歐式距離、曼哈頓距離等等，滿足條件：

則稱D(,)是位置敏感的。

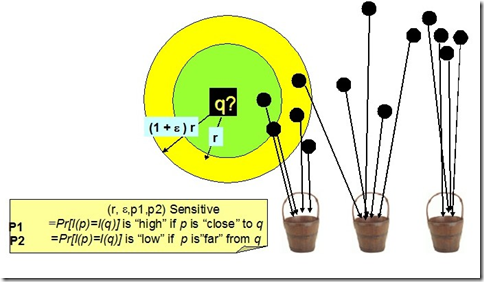
如下圖，空間上的點經位置敏感雜湊函式雜湊之後，對於q，其rNN有可能雜湊到同一個桶（如第一個桶）,即雜湊到第一個桶的概率較大，會大於某一個概率閾值p1;而其(1+emxilong)rNN之外的物件則不太可能雜湊到第一個桶，即雜湊到第一個桶的概率很小，會小於某個閾值p2.

LSH的作用

◆高維下近似查詢

相似性檢索在各種領域特別是在視訊、音訊、影象、文字等含有豐富特徵資訊領域中的應用變得越來越重要。豐富的特徵資訊一般用高維向量表示，由此相似性檢索一般通過K近鄰或近似近鄰查詢來實現。一個理想的相似性檢索一般需要滿足以下四個條件：

1. 高準確性。即返回的結果和線性查詢的結果接近。

2. 空間複雜度低。即佔用記憶體空間少。理想狀態下，空間複雜度隨資料集呈線性增長，但不會遠大於資料集的大小。

3. 時間複雜度低。檢索的時間複雜度最好為O（1）或O（logN)。

4. 支援高維度。能夠較靈活地支援高維資料的檢索。

傳統主要方法是基於空間劃分的演算法——tree類似演算法，如R-tree，Kd-tree，SR-tree。這種演算法返回的結果是精確的，但是這種演算法在高維資料集上的時間效率並不高。實驗[1]指出維度高於10之後，基於空間劃分的演算法時間複雜度反而不如線性查詢。LSH方法能夠在保證一定程度上的準確性的前提下，時間和空間複雜度得到降低，並且能夠很好地支援高維資料的檢索。

◆分類和聚類

根據LSH的特性，即可將相近（相似）的物件雜湊到同一個桶之中，則可以對影象、音視訊、文字等豐富的高維資料進行分類或聚類。

◆資料壓縮。如廣泛地應用於訊號處理及資料壓縮等領域的Vector Quantization量子化技術。

總而言之，哪兒需要近似kNN查詢，哪兒都能用上LSH.

[1] Weber R, Schek H, Blott S. A quantitative analysis and performance study for similarity search methods in high dimensional spaces Proc.of the 24th Intl.Conf.on Very Large Data Bases (VLDB).1998:194-205

原理及過程

原文連結http://www.cnblogs.com/hxsyl/p/4518506.html

馬克·吐溫曾經說過，所謂經典小說，就是指很多人希望讀過，但很少人真正花時間去讀的小說。這種說法同樣適用於“經典”的計算機書籍。

　　最近一直在看LSH，不過由於matlab基礎比較差，一直沒搞懂。最近看的論文裡幾乎都是用simHash來實現LSH，從而進行ANN。

　　有空看看基於滑動視窗的論文相似性檢測。

　　如何用matlab畫出一個數列（函式）的收斂過程（菱形收斂、圓形收斂）？

　　學完分散式了，我打算自己學WordPress，建立自己的獨立部落格，放在雲平臺或者伺服器空間，然後學著分析流量和負載均衡這一類，這也算是資料探勘了吧。

　　我的學習目標：像吳軍博士一樣深入淺出地講解出來一個知識點，這需要很深厚的積累，我以前寫的《徹底弄懂最短路徑問題》，自己感覺挺不錯的，網友反饋也不錯；雖然說實踐和理論相輔相成，筆者個人覺得鮮血little理論，再搞many實踐，最後在學much理論，進而繼續指導實踐，螺旋遞增式學習。

一.基礎知識

1.1 Java位運算

　　位運算只適合整數哦。。。因為浮點的儲存方案決定不能位運算，如果非要位運算，就需要Float.floatToIntBits，運算完，再通過Float.intBitsToFloat轉化回去。(java預設的float,double的hashcode其實就是對應的floatToIntBits的int值)

1.2 Java中浮點數比較大小

　　C++用fabs函式，Java中用Double.doubleToLongBits函式，然後直接比較大小，內部原理不做探討。

1.3 StringTokenzier

　　Java中substring方法可以分解字串，返回的是原字串的一個子字串。如果要講一個字串分解為一個一個的單詞或者標記，StringTokenizer可以幫你。

　　StringTokenizer確實更快些，至於為什麼jdk裡不推薦使用了，還要再研究（現在是split結合正則表示式）。
　　測試方法：用StringBuilder的append方法，構造100W字串，然後分別分別測試並算時間就ok了。

1.4 偶然所得

　　final可以不再定義時候初始化，好像可以再構造方法裡初始化。

二.simHash演算法簡介

　　1、分詞，把需要判斷文字分詞形成這個文章的特徵單詞。最後形成去掉噪音詞的單詞序列併為每個詞加上權重，我們假設權重分為5個級別（1~5）。比如：“ 美國“51區”僱員稱內部有9架飛碟，曾看見灰色外星人 ” ==> 分詞後為 “ 美國（4） 51區（5） 僱員（3） 稱（1） 內部（2） 有（1） 9架（3） 飛碟（5） 曾（1） 看見（3） 灰色（4） 外星人（5）”，括號裡是代表單詞在整個句子裡重要程度，數字越大越重要。

　　2、hash，通過hash演算法把每個詞變成hash值，比如“美國”通過hash演算法計算為 100101,“51區”通過hash演算法計算為 101011。這樣我們的字串就變成了一串串數字，還記得文章開頭說過的嗎，要把文章變為數字計算才能提高相似度計算效能，現在是降維過程進行時。

　　3、加權，通過 2步驟的hash生成結果，需要按照單詞的權重形成加權數字串，比如“美國”的hash值為“100101”，通過加權計算為“4 -4 -4 4 -4 4”；“51區”的hash值為“101011”，通過加權計算為 “ 5 -5 5 -5 5 5”。

　　4、合併，把上面各個單詞算出來的序列值累加，變成只有一個序列串。比如 “美國”的 “4 -4 -4 4 -4 4”，“51區”的 “ 5 -5 5 -5 5 5”， 把每一位進行累加， “4+5 -4+-5 -4+5 4+-5 -4+5 4+5” ==》 “9 -9 1 -1 1 9”。這裡作為示例只算了兩個單詞的，真實計算需要把所有單詞的序列串累加。

　　5、降維，把4步算出來的 “9 -9 1 -1 1 9” 變成 0 1 串，形成我們最終的simhash簽名。 如果每一位大於0 記為 1，小於0 記為 0。最後算出結果為：“1 0 1 0 1 1”。

三.演算法幾何意義及原理

3.1 幾何意義

　　這個演算法的幾何意義非常明瞭。它首先將每一個特徵對映為f維空間的一個向量，這個對映規則具體是怎樣並不重要，只要對很多不同的特徵來說，它們對所對應的向量是均勻隨機分佈的，並且對相同的特徵來說對應的向量是唯一的就行。比如一個特徵的4位hash簽名的二進位制表示為1010，那麼這個特徵對應的 4維向量就是(1, -1, 1, -1)T，即hash簽名的某一位為1，對映到的向量的對應位就為1，否則為-1。然後，將一個文件中所包含的各個特徵對應的向量加權求和，加權的係數等於該特徵的權重。得到的和向量即表徵了這個文件，我們可以用向量之間的夾角來衡量對應文件之間的相似度。最後，為了得到一個f位的簽名，需要進一步將其壓縮，如果和向量的某一維大於0，則最終簽名的對應位為1，否則為0。這樣的壓縮相當於只留下了和向量所在的象限這個資訊，而64位的簽名可以表示多達264個象限，因此只儲存所在象限的資訊也足夠表徵一個文件了。

3.2 演算法原理描述性證明

　　明確了演算法了幾何意義，使這個演算法直觀上看來是合理的。但是，為何最終得到的簽名相近的程度，可以衡量原始文件的相似程度呢？這需要一個清晰的思路和證明。在simhash的發明人Charikar的論文中並沒有給出具體的simhash演算法和證明，以下列出我自己得出的證明思路。
　　Simhash是由隨機超平面hash演算法演變而來的，隨機超平面hash演算法非常簡單，對於一個n維向量v，要得到一個f位的簽名(f<<n)，演算法如下：
　　1，隨機產生f個n維的向量r1,…rf；
　　2，對每一個向量ri，如果v與ri的點積大於0，則最終簽名的第i位為1，否則為0.
　　這個演算法相當於隨機產生了f個n維超平面，每個超平面將向量v所在的空間一分為二，v在這個超平面上方則得到一個1，否則得到一個0，然後將得到的 f個0或1組合起來成為一個f維的簽名。如果兩個向量u, v的夾角為θ，則一個隨機超平面將它們分開的概率為θ/π，因此u, v的簽名的對應位不同的概率等於θ/π。所以，我們可以用兩個向量的簽名的不同的對應位的數量，即漢明距離，來衡量這兩個向量的差異程度。
　　Simhash演算法與隨機超平面hash是怎麼聯絡起來的呢？在simhash演算法中，並沒有直接產生用於分割空間的隨機向量，而是間接產生的：第 k個特徵的hash簽名的第i位拿出來，如果為0，則改為-1，如果為1則不變，作為第i個隨機向量的第k維。由於hash簽名是f位的，因此這樣能產生 f個隨機向量，對應f個隨機超平面。下面舉個例子：
　　假設用5個特徵w1,…,w5來表示所有文件，現要得到任意文件的一個3維簽名。假設這5個特徵對應的3維向量分別為：
　　h(w1) = (1, -1, 1)T
　　h(w2) = (-1, 1, 1)T
　　h(w3) = (1, -1, -1)T
　　h(w4) = (-1, -1, 1)T
　　h(w5) = (1, 1, -1)T
　　按simhash演算法，要得到一個文件向量d=(w1=1, w2=2, w3=0, w4=3, w5=0) T的簽名，
先要計算向量m = 1*h(w1) + 2*h(w2) + 0*h(w3) + 3*h(w4) + 0*h(w5) = (-4, -2, 6) T，然後根據simhash演算法的步驟3，得到最終的簽名s=001。上面的計算步驟其實相當於，先得到3個5維的向量，第1個向量由h(w1),…,h(w5)的第1維組成：r1=(1,-1,1,-1,1) T；第2個5維向量由h(w1),…,h(w5)的第2維組成：r2=(-1,1,-1,-1,1) T；同理，第3個5維向量為：r3=(1,1,-1,1,-1) T.按隨機超平面演算法的步驟2，分別求向量d與r1,r2,r3的點積:

　　d T r1=-4 < 0，所以s1=0;
　　d T r2=-2 < 0，所以s2=0;
　　d T r3=6 > 0，所以s3=1.　　故最終的簽名s=001，與simhash演算法產生的結果是一致的。
　　從上面的計算過程可以看出，simhash演算法其實與隨機超平面hash演算法是相同的，simhash演算法得到的兩個簽名的漢明距離，可以用來衡量原始向量的夾角。這其實是一種降維技術，將高維的向量用較低維度的簽名來表徵。衡量兩個內容相似度，需要計算漢明距離，這對給定簽名查詢相似內容的應用來說帶來了一些計算上的困難；我想，是否存在更為理想的simhash演算法，原始內容的差異度，可以直接由簽名值的代數差來表示呢？

　　參考http://blog.sina.com.cn/s/blog_72995dcc010145ti.html

四.演算法與網頁去重

　　例如，文字的特徵可以選取分詞結果，而權重可以用df來近似。
　　Simhash具有兩個“衝突的性質”：
　　1. 它是一個hash方法
　　2. 相似的文字具有相似的hash值，如果兩個文字的simhash越接近，也就是漢明距離越小，文字就越相似。
　　因此海量文字中查重的任務轉換位如何在海量simhash中快速確定是否存在漢明距離小的指紋。也就是：在n個f-bit的指紋中，查詢漢明距離小於k的指紋。
在文章的實驗中，simhash採用64位的雜湊函式。在80億網頁規模下漢明距離=3剛好合適。
因此任務的f-bit=64 , k=3 , n= 8*10^11
　　任務清晰，首先看一下兩種很直觀的方法：
　　1. 枚舉出所有漢明距離小於3的simhash指紋，對每個指紋在80億排序指紋中查詢。（這種方法需要進行C（64，3）=41664詞的simhash指紋，再為每個進行一次查詢）
　　2. 所有接近的指紋排序到一起，這至多有41664排序可能，需要龐大的空間。提出的方法介於兩者之間，合理的空間和時間的折中。
　　假設我們有一個已經排序的容量為2d，f-bit指紋集。看每個指紋的高d位。該高低位具有以下性質：儘管有很多的2d位組合存在，但高d位中有隻有少量重複的。
　　現在找一個接近於d的數字d’，由於整個表是排好序的，所以一趟搜尋就能找出高d’位與目標指紋F相同的指紋集合f’。因為d’和d很接近，所以找出的集合f’也不會很大。
　　最後在集合f’中查詢 和F之間海明距離為k的指紋也就很快了。
　　總的思想：先要把檢索的集合縮小，然後在小集合中檢索f-d’位的海明距離
按照例子，80億網頁 有2^34 個，那麼理論上34位就能表示完80億不重複的指紋。我們假設最前的34位的表示完了80億指紋，假設指紋在前30位是一樣的，那麼後面4位還可以表示24個， 只需要逐一比較這16個指紋是否於待測指紋漢明距離小於3。
　　假設：對任意34位中的30位都可以這麼做。
　　因此在一次完整的查詢中，限定前q位精確匹配（假設這些指紋已經是q位有序的，可以採用二分查詢，如果指紋量非常大，且分佈均勻，甚至可以採用內插搜尋），之後的2d-q個指紋剩下64-q位需要比較漢明距離小於3。
　　於是問題就轉變為如何切割64位的q。
　　將64位平分成若干份，例如4份ABCD，每份16位。
　　假設這些指紋已經按A部分排序好了，我們先按A的16位精確匹配到一個區間，這個區間的後BCD位檢查漢明距離是否小於3。
　　同樣的假設，其次我們按B的16位精確匹配到另一個區間，這個區間的所有指紋需要在ACD位上比較漢明距離是否小於3。
　　同理還有C和D，所以這裡我們需要將全部的指紋T複製4份， T1 T2 T3 T4， T1按A排序，T2按B排序… 4份可以並行進行查詢，最後把結果合併。這樣即使最壞的情況：3個位分別落在其中3個區域ABC,ACD,BCD,ABD…都不會被漏掉。

　　只精確匹配16位，還需要逐一比較的指紋量依然龐大，可能達到2d-16個，我們也可以精確匹配更多的。
　　例如：將64位平分成4份ABCD，每份16位，在BCD的48位上，我們再分成4份，WXZY，每份12位， 漢明距離的3位可以散落在任意三塊，那麼A與WXZY任意一份合起來做精確的28位…剩下3份用來檢查漢明距離。 同理B，C，D也可以這樣，那麼T需要複製16次，ABCD與WXYZ的組合做精確匹配，每次精確匹配後還需要逐一比較的個數降低到2d-28個。不同的組合方式也就是時間和空間上的權衡。
　　最壞情況是其中3份可能有1位漢明距離差異為1。
　　演算法的描述如下：
　　1）先複製原表T為Tt份：T1,T2,….Tt
　　2）每個Ti都關聯一個pi和一個πi，其中pi是一個整數, πi是一個置換函式，負責把pi個bit位換到高位上。
　　3）應用置換函式πi到相應的Ti表上，然後對Ti進行排序
　　4）然後對每一個Ti和要匹配的指紋F、海明距離k做如下運算：
　　　　a) 然後使用F’的高pi位檢索，找出Ti中高pi位相同的集合
　　　　b) 在檢索出的集合中比較f-pi位，找出海明距離小於等於k的指紋
　　5）最後合併所有Ti中檢索出的結果
　　由於文字已經壓縮成8個位元組了，因此其實Simhash近似查重精度並不高：

 　　筆者注：這個方法是第二次看了，還是不甚理解........講解不夠直觀明瞭..........

五.演算法Java實現

　　想了很久，覺得直接放程式碼是個不好的習慣，容易依賴別人，所以筆者放在CSDN上，不過只需要1分。

六.結束語及參考文獻

6.1 結束語

　　熬夜感覺並不好，如何才能戒掉這個壞習慣。

　　谷歌真叼......

　　筆者會在下一篇博文裡探討simHash和VSM與網頁去重。

　　探討資訊檢索與跳躍表。

　　探討二分圖最大權匹配（這個應用比較廣吧，感覺可以用來精確投放廣告，靈感來自計算機121教師和課程互選）。

6.2  部分參考文獻

　　http://blog.sina.com.cn/s/blog_72995dcc010145ti.html

　　http://gemantic.iteye.com/blog/1701101

　　http://blog.csdn.net/lgnlgn/article/details/6008498

　　http://blog.csdn.net/meijia_tts/article/details/7928579

　　論文Detecting near-duplicates for web crawling.