區域性敏感雜湊LSH(Locality-Sensitive Hashing)——海量資料相似性查詢技術
一、 前言
最近在工作中需要對海量資料進行相似性查詢,即對微博全量使用者進行關注相似度計算,計算得到每個使用者關注相似度最高的TOP-N個使用者,首先想到的是利用簡單的協同過濾,先定義相似性度量(cos,Pearson,Jaccard),然後利用通過兩兩計算相似度,計算top-n進行篩選,這種方法的時間複雜度為\(O(n^2)\)(對於每個使用者,都和其他任意一個使用者進行了比較)但是在實際應用中,對於億級的使用者量,這個時間複雜度是無法忍受的。同時,對於高維稀疏資料,計算相似度同樣很耗時,即\(O(n^2)\)的係數無法省略。這時,我們便需要一些近似演算法,犧牲一些精度來提高計算效率,在這裡簡要介紹一下MinHashing,LSH,以及Simhash。
二、 MinHashing
Jaccard係數是常見的衡量兩個向量(或集合)相似度的度量:
\[ J(A,B)=\frac {\left | A\cap B \right |}{\left | A\cup B \right |} \]
為方便表示,我們令A和B的交集的元素數量設為\(x\),A和B的非交集元素數量設為\(y\),則Jaccard相似度即為\()\frac x {(x+y)}\)。
所謂的MinHsah,即進行如下的操作:
對A、B的\(n\)個維度,做一個隨機排列(即對索引\(,i_1,i_2,i_3,\cdots,i_n\)隨機打亂)
分別取向量A、B的第一個非0行的索引值(\(index\)),即為MinHash值
得到AB的MinHash值後,可以有以下一個重要結論:
\[ P[minHash(A) = minHash(B)] = Jaccard(A,B) \]
以下是證明:
在高維稀疏向量中,考慮AB在每一維的取值分為三類:
A、B均在這一維取1(對應上述元素個數為\(x\))
A、B只有一個在這一維取1(對應上述元素個數為\(y\))
A、B均取值為0
其中,第三類佔絕大多數情況,而這種情況對MinHash值無影響,第一個非零行屬於第一類的情況的概率為\(()\frac x{(x+y)}\),從而上面等式得證。
另外,按照排列組合的思想,全排列中第一行為第一類的情況為\(()(x*(x+y-1)!)\),全排列為\((x+y)!\),即將\(n\)維向量全排列之後,對應的minHash值相等的次數即為Jaccard相似度。
但是在實際情況中,我們並不會做\((x+y)!\)次排列,只做\(m\)次(\(m\)一般為幾百或者更小,通常遠小於\(n\)),這樣,將AB轉為兩個\(m\)維的向量,向量值為每次排列的MinHash值。
\[
sig(A)=[h_1(A),h_2(A),\cdots,h_m(A)]
\]
\[ sig(B)=[h_1(B),h_2(B),\cdots,h_m(B)] \]
這樣計算兩個Sig向量相等的比例,即可以估計AB的Jaccard相似度(近似保持了AB的相似度,但是不能完全相等,除非全排列,對於這種利用相似變換相似空間的方法,需要設計雜湊函式,而一般的雜湊函式無法將滿足相似向量雜湊後的值相似)。
在實際實現中,m次排列通常通過一個針對索引的雜湊來達到hash的效果,即MinHashing演算法(實現可參考Spark實現細節
http://spark.apache.org/docs/2.2.0/api/java/org/apache/spark/ml/feature/MinHashLSH.html)
三、LSH
上面的MinHashing解決了高維稀疏向量的運算,但是計算兩兩使用者的相似度,其時間複雜度仍然是O(n^2),顯然這個計算量還沒有得到改善,這時我們如果能將使用者分到不同的桶,只比較可能相似的使用者,即相似使用者以較大可能分到同一個桶內,這樣不相似的使用者基本不會發生比較,降低計算複雜度,LSH即為這樣的方法。
LSH方法基於這樣的思想:在原空間中很近(相似)的兩個點,經過LSH雜湊函式的對映後,有很大概率它們的雜湊是一樣的;而兩個離的很遠(不相似)的兩個點,對映後,它們的雜湊值相等的概率很小。
基於這樣的思想,LSH選擇的雜湊函式即需要滿足下列性質:
對於高維空間的任意兩點,\(,x,y\):
如果\(d(x,y)≤R\),則\(h(x)=h(y)\)的概率不小於\(P_1\)
如果\(d(x,y)≥cR\),則\(h(x)=h(y)\)的概率不大於\(P_2\)。
其中,\(c>1,P_1>P_2\)。滿足這樣性質的雜湊函式,被稱為 \((R,cR,P1,P2)-sensive\)。
本文介紹的LSH方法基於MinHashing函式。
LSH將每一個向量分為幾段,稱之為band,如下圖\(^6\)
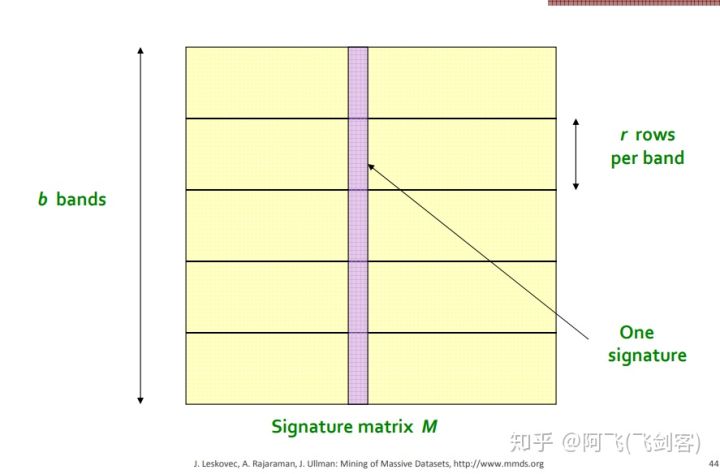
每一個向量在圖中被分為了\(b\)段(每一列為一個向量),每一段有\(r\)行(個)MinHash值。在任意一個band中分到了同一個桶內,就成為候選相似使用者(擁有較大可能相似)。
設兩個向量的相似度為\(t\),則其任意一個band所有行相同的概率為\(t^r\),至少有一行不同的概率為\(1-t^r\), 則所有band都不同的概率為\(()(1-t^r)^b\),至少有一個band相同的概率為\(()1-(1-t^r)^b\)。其曲線如下圖所示\(^6\)
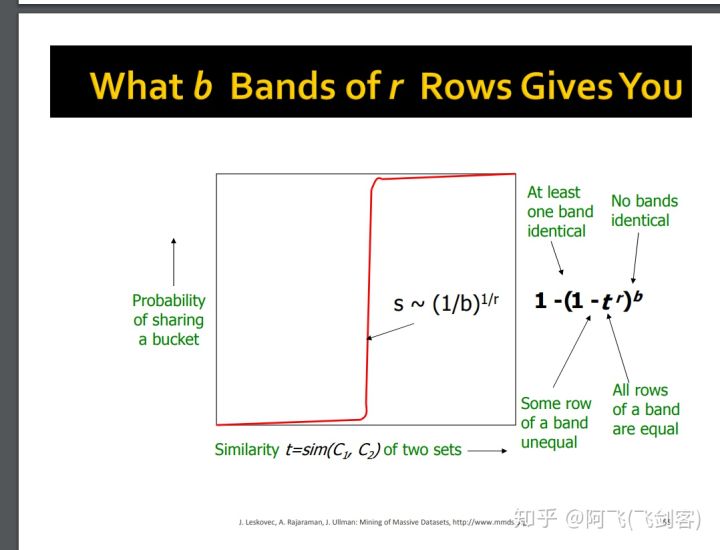
圖中變化最抖的點s近似為\((\frac 1 b)^{\frac 1 r}\),其中,s作為閾值為具體為多少是我們才將其分到一個桶中,即人工設定s來確定這裡的b和r。如圖例,對於\(r=5,b=10\)時,其閾值為0.6,其中,綠色為假正例率(相似度很低的兩個使用者被雜湊到同一個桶內),藍色為假負例率(真正相似的使用者在每一個band上都沒有被雜湊到同一個桶內),可以設定\(,b,r\)調整\(s\),\(s\)越大,效率越高,假正例率越低,假負例率越高。
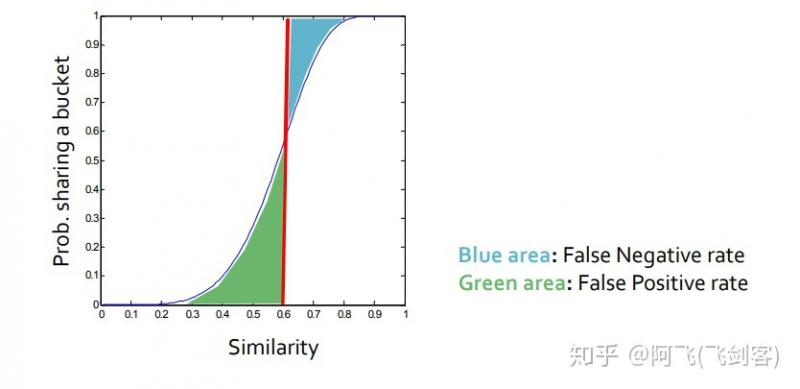
四、後記
接觸LSH是一個很偶然的工作中的小需求,感慨其在海量高維稀疏資料中有很好的應用場景(文字,圖片,結構資料均可以用),速度快,計算複雜度低,感慨其embedding轉換的巧妙,鑑於本人水平和精力著實有限,沒有搞懂的地方其實還很多,沒有證明MinHashing方法滿足LSH方法的性質,也沒有搞懂BloomFilter算不算也是一種LSH方法的雜湊函式。知乎使用者@hunter7z的答案給了我不少的啟發 ,感謝。
查了很多資料,作此讀書筆記,權且拋磚引玉。
參考文獻:
- http://www.mmds.org/
- https://zhuanlan.zhihu.com/p/46164294
- http://spark.apache.org/docs/2.2.0/api/java/org/apache/spark/ml/feature/MinHashLSH.html
- http://mlwiki.org/index.php/Locality_Sensitive_Hashing
- https://www.cnblogs.com/wangguchangqing/p/9796226.html
http://www.mmds.org/mmds/v2.1/ch03-lsh.pdf
本文由飛劍客原創,如需轉載,請聯絡私信聯絡知乎:@AndyChanCD
