//原文：http://blog.csdn.net/google0802/article/details/8938849

插值演算法對於縮放比例較小的情況是完全可以接受的，令人信服的。一般的，縮小0.5倍以上或放大3.0倍以下，對任何影象都是可以接受的。常用的插值方法有:最近鄰插值法，雙線性插值法，三次卷積插值法。

1.最近鄰插值法（Nearest Neighbor Interpolation）

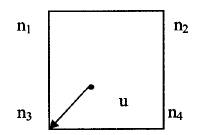
        最近鄰插值法又稱零階插值,該方法取距離輸出影象上的畫素點對映到輸入影象上的位置最近的輸入畫素的顏色值(或灰度值)作為輸出影象上畫素點的顏色值(或灰度值)。如圖1所示,最近鄰插值法直接計算輸出畫素對映到輸入影象座標系下的點u和近鄰四點(n1,n2,n3,n4)之間的距離,取距離u最近的畫素點的顏色值(或灰度值)賦給u。

       g(x',y')=f(int(x十0.5),int(y+0.5))     -------------------(1)             
       公式(1)為最近鄰插值的具體計算公式。其中g(x',y')為輸出影象中座標為(x',y')的畫素點的顏色值(或灰度值)，f(x,y)為輸入影象中座標為(x,y)的畫素點的顏色值(或灰度值),(x,y)為輸出影象上的座標(x',y')對映到輸入影象座標系下的座標。int(x)為取整運算。

2.雙線性插值法(Bilinear Interpolation)

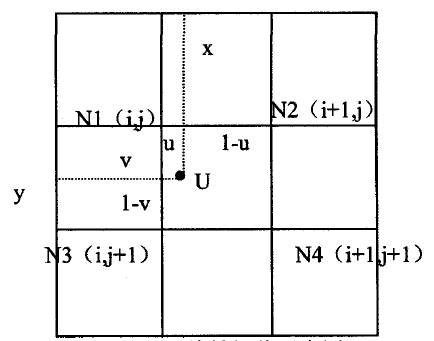
雙線性插值法又稱一階插值,利用輸入影象中與輸出影象畫素點對映位置最鄰近的4個畫素點的顏色值(或灰度值)計算輸出影象中畫素點的顏色值(或灰度值)。如圖2所示

圖2中,假設輸出影象上的一個畫素點g(x',y')其座標為(x',y'),它對映到輸入影象中的點u其座標為(x,y)。n1,n2,n3,n4為與點u最鄰近的四個點,其座標分別為(i,j)，(i+1,j)，(i,j+1)，(i+1,j+1)，顏色值(或灰度值)分別為f(i,j)，f(i+1,j)，f(i,j+1)，f(i+1,j+1)。則雙線性插值的計算公式為公式(2),其中u=(x-i)，v=(y-j)。
g(x',y')=(1-u)(1-v)f(i,j) + u(1-v)f(i+1,j) + (1-u)vf(i,j+1) + uvf(i+1,j+1)  ---------------(2)

3.三次卷積插值法

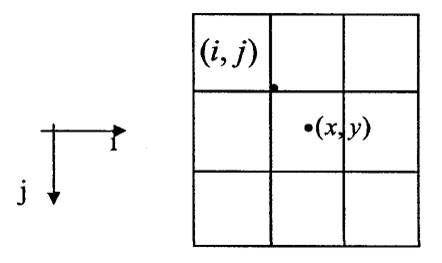
為了得到更精確的(x',y')的顏色值(或灰度值)g(x',y'),就不僅需要考慮與(x',y')點最鄰近的四個點對它的影響,還要考慮到該點周圍16個相鄰點的顏色值(或灰度值)對它的影響。如圖3所示。

 由連續訊號取樣定理可知,若對取樣值用插值函式s(x)=sin(πx)/(πx)插值,則可以準確地恢復原函式,也就是說可以準確地得到取樣點間任意點的值"三次卷積插值法實質上就是利用一個三次多項式來近似理論上最佳插值函式S(x),如公式(3)。

         -----------(3)

目的畫素值f(i+u,j+v)可由如下插值公式得到：

　　　　f(i+u,j+v) = [A] * [B] * [C]

其中：

[A]=[ S(u + 1)　S(u + 0)　S(u - 1)　S(u - 2) ]

　　       ┏     f(i-1, j-1)　 f(i-1, j+0)　 f(i-1, j+1)　 f(i-1, j+2)   ┓
        [B]=┃     f(i+0, j-1)　f(i+0, j+0)　f(i+0, j+1)　f(i+0, j+2)  ┃
　　       ┃     f(i+1, j-1)　f(i+1, j+0)　f(i+1, j+1)　f(i+1, j+2)  ┃
　　       ┗     f(i+2, j-1)　f(i+2, j+0)　f(i+2, j+1)　f(i+2, j+2)  ┛

　　        ┏   S(v + 1)  ┓
        [C]=┃   S(v + 0)  ┃
　　        ┃   S(v - 1)   ┃
　　        ┗   S(v - 2)   ┛

        不同的插值方法,具有不同的特點和優缺點"最鄰近插值法計算簡單,工作量小,但處理後的影象邊緣容易產生鋸齒效應造成影象的不連續;三次卷積插值法帶有邊緣增強的效果,能夠較好的保持影象的細微結構,但計算量很大;雙線性插值法克服了最鄰近法不連續的缺點,計算較三次卷積法簡單,但邊緣受到平滑作用出現輪廓模糊現象。