詳解協方差與協方差矩陣
協方差的定義
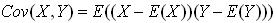
對於一般的分佈,直接代入E(X)之類的就可以計算出來了,但真給你一個具體數值的分佈,要計算協方差矩陣,根據這個公式來計算,還真不容易反應過來。網上值得參考的資料也不多,這裡用一個例子說明協方差矩陣是怎麼計算出來的吧。
記住,X、Y是一個列向量,它表示了每種情況下每個樣本可能出現的數。比如給定
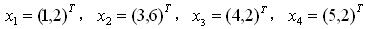
則X表示x軸可能出現的數,Y表示y軸可能出現的。注意這裡是關鍵,給定了4個樣本,每個樣本都是二維的,所以只可能有X和Y兩種維度。所以
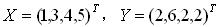
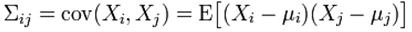
用中文來描述,就是:
協方差(i,j)=(第i列的所有元素-第i列的均值)*(第j列的所有元素-第j列的均值)
這裡只有X,Y兩列,所以得到的協方差矩陣是
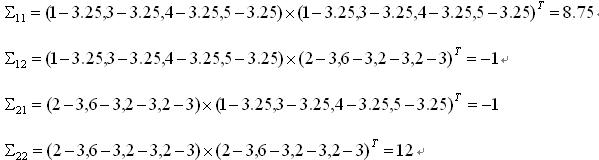
所以,按照定義,給定的4個二維樣本的協方差矩陣為:
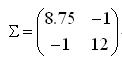
用matlab計算這個例子
z=[1,2;3,6;4,2;5,2]
cov(z)
ans =
2.9167-0.3333
-0.33334.0000
可以看出,matlab計算協方差過程中還將元素統一縮小了3倍。所以,協方差的matlab計算公式為:
協方差(i,j)=(第i列所有元素-第i列均值)*(第j列所有元素-第j列均值)/(樣本數-1)
下面在給出一個4維3樣本的例項,注意4維樣本與符號X,Y就沒有關係了,X,Y表示兩維的,4維就直接套用計算公式,不用X,Y那麼具有迷惑性的表達了。


(3)與matlab計算驗證
Z=[1 2 3 4;3 4 1 2;2 3 1 4]
cov(Z)
ans =
1.00001.0000-1.0000-1.0000
1.00001.0000-1.0000-1.0000
-1.0000-1.00001.33330.6667
-1.0000-1.00000.66671.3333
可知該計算方法是正確的。我們還可以看出,協方差矩陣都是方陣,它的維度與樣本維度有關(相等)。參考2中還給出了計算協方差矩陣的原始碼,非常簡潔易懂,在此感謝一下!
參考:
[1] http://en.wikipedia.org/wiki/Covariance_matrix
[2] http://www.cnblogs.com/cvlabs/archive/2010/05/08/1730319.html
相關推薦
詳解協方差與協方差矩陣
協方差的定義 對於一般的分佈,直接代入E(X)之類的就可以計算出來了,但真給你一個具體數值的分佈,要計算協方差矩陣,根據這個公式來計算,還真不容易反應過來。網上值得參考的資料也不多,這裡用一個例子說
【數學基礎】 協方差與協方差矩陣
##常見的統計量 在概率與統計中,最常見的統計量有樣本均值、方差、標準差、極差以及中位數等等。這些都是最基礎、最常見的統計量。 均值: Xˉ=1n∑i=1nXi\bar{X}=\frac{1}{n}\sum_{i=1}^{n}X_{i}
方差與樣本方差、協方差與樣本協方差
0. 獨立變數乘積的方差 獨立變數積的方差與各自期望方差的關係: Var(XY)=[E(X)]2Var(Y)+[E(Y)]2Var(X)+Var(X)Var(Y)=[E(X)]2Var(Y)+[E
協方差與協方差矩陣
統計學的基本概念 學過概率統計的孩子都知道,統計裡最基本的概念就是樣本的均值,方差,或者再加個標準差。首先我們給你一個含有n個樣本的集合X={X1,…,Xn}XX1Xn,依次給出這些概念的公式描述,這些高中學過數學的孩子都應該知道吧,一帶而過。 均值: X¯=∑ni=
樣本服從正態分布,證明樣本容量n乘樣本方差與總體方差之比服從卡方分布x^2(n)
htm http ges .cn www align 中心 log lang 樣本服從正態分布,證明樣本容量n乘樣本方差與總體方差之比服從卡方分布x^2(n) 正態分布的n階中心矩參見: http://www.doc88.com/p-334742692198.ht
統計學---之樣本方差與總體方差的區別
前段日子重新整理了一下這個問題的解答,跟大家分享一下,如果有什麼錯誤的話希望大家能夠提出來,我會及時改正的,話不多說進入正題: 首先,我們來看一下樣本方差的計算公式: &nbs
樣本方差與總體方差
一、方差(variance):衡量隨機變數或一組資料時離散程度的度量。 概
方差與樣本方差的區別?為什麼方差是除以N,樣本方差是除以N-1
1.研究某隨機變數的方差,有無窮多個樣本,可以通過抽取一個樣本集,以它的方差作為該隨機變數方差的估計。 當該樣本集的樣本數N趨於正無窮時,可以證明除以N-1才是無偏的,即收斂於該隨機變數的方差;除以N是有偏的。 因此採用無偏估計時除以N-1,而不是除以N。 2.僅研
#51CTO學院四周年#詳解JWT的結構與應用
json 升職啦 技能 1. JWT是什麽?JWT,全稱JSON WEB TOKEN, 是WEB客戶端與服務器之間相互進行安全通信的規範。通信雙方的對象本身通過JSON傳遞數據是不安全的,但是由於有了數字簽名的存在,這些信息變的可信的。2. JWT特點簡潔(Compact): 可以通過URL,PO
詳解web容器 - Jetty與Tomcat孰強孰弱
open() 等待 category 架構設計 eth div cte 內部 非阻塞 本文引用http://www.cnblogs.com/crazyacking/p/5734849.html Jetty 基本架構 體系結構 啟動過程 接受請求 基於 H
TCP詳解——連接建立與斷開
介紹 32bit 標誌位 關閉連接 選擇 tro 窗口大小 syn 重新發送 一、報文結構介紹 在開始講TCP連接過程時,還是先看看TCP報文的格式如圖1所示。IP數據報此時由IP頭部+TCP頭部+TCP數據組成。不帶選項的TCP頭部是20字節長,而帶選項的,TCP頭部
js內存空間 執行上下文 變量對象詳解 作用域鏈與閉包 全方位解讀this
變量 詳解 tail bsp pin 上下 AR detail net 內存空間:https://blog.csdn.net/pingfan592/article/details/55189622 執行上下文:https://blog.csdn.net/pingfan592
詳解MySQL用戶與授權、MySQL日誌管理、數據亂碼解決方案。
服務 defaults 速查 col pda pro 創建 接下來 方案 數據庫是信息系統中非常重要的環節,合理高效的對它進行管理是很重要的工作。通常是由總管理員創建不同的管理賬戶,然後分配不同的操作權限,把這些賬戶交給相應的管理人員使用。本篇我們在CentOS7.5操作系
WebSocket安卓客戶端實現詳解(一)--連線建立與重連
前言 這裡特別說明下因為WebSocket服務端是公司線上專案所以這裡url和具體協議我全部抹去了,但我會盡力給大家講明白並且demo我都是測試過,還望各位看官見諒 我們先粗獷的講下流程,掌握個大概的方向,然後在深入講解細節的實現.這裡先解答一個疑惑,為啥我們這要用WebSocket而不
網路學習之路之基礎詳解① 之 計算機網路與Internet
網路學習之路之基礎詳解① 計算機網路概述之整體瞭解 首先我們理清總體思路,來看看計算機網路概述整體的框圖 從上圖我們可以大致瞭解到計算機網路包含內容,下面我們來對各方面進行詳細學習: (1)計算機網路VS Internet ①基礎理解: 計算機網路:一些互相連線的,自治的計算機的
詳解JVM記憶體管理與垃圾回收機制1 - 記憶體管理
Java應用程式是執行在JVM上的,得益於JVM的記憶體管理和垃圾收集機制,開發人員的效率得到了顯著提升,也不容易出現記憶體溢位和洩漏問題。但正是因為開發人員把記憶體的控制權交給了JVM,一旦出現記憶體方面的問題,如果不瞭解JVM的工作原理,將很難排查錯誤。本文將從理論角度介紹虛擬機器的記憶
詳解JVM記憶體管理與垃圾回收機制2 - 何為垃圾
隨著程式語言的發展,GC的功能不斷增強,效能也不斷提高,作為語言背後的無名英雄,GC離我們的工作似乎越來越遠。作為Java程式設計師,對這一點也許會有更深的體會,我們不需要了解太多與GC相關的知識,就能很好的完成工作。那還有必要深入瞭解GC嗎?學習GC的意義在哪兒? 不管效能提高到何種程
Delphi 中的 XMLDocument 類詳解(9) - 關於 HasChildNodes 與 IsTextElement
unit Unit1; interface uses Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms, Dialogs, xmldom, XMLIntf, msxmldom, X
【Vue】詳解元件的基礎與高階用法
構建元件 元件基礎 一個元件由 template、data、computed、methods等選項組成。需要注意: template 的 DOM 結構必須有根元素 data 必須是函式,資料通過 return 返回出去 // 示例:定義一個元件 MyCompon
詳解vue全域性元件與區域性元件使用方法
這篇文章主要為大家詳細介紹了vue全域性元件與區域性元件的使用方法,具有一定的參考價值,對此有需要的朋友可以參考學習下。如有不足之處,歡迎批評指正。 vue全域性/區域性註冊,以及一些混淆的元件main.js入口檔案的一些常用配置, 在入口檔案上定義的public.vue為全域性元件,在這裡用的是pug模版
