Multiply Strings(高精度乘法)

【難度：Medium】
Given two numbers represented as strings, return multiplication of the numbers as a string.

Note: The numbers can be arbitrarily large and are non-negative.
實現高精度非負整數乘法。

解題思路

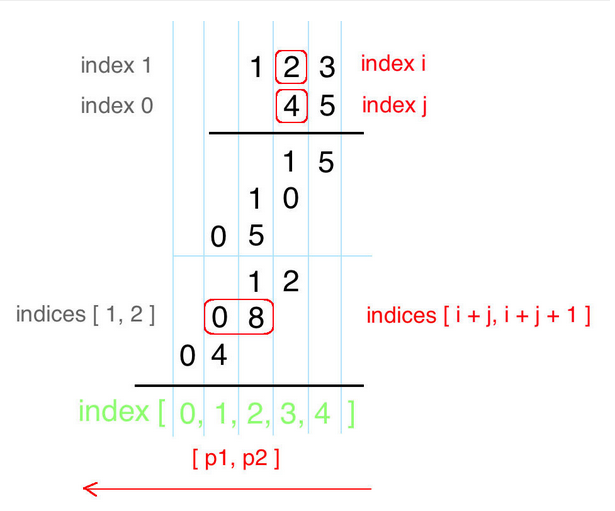
按照常規解法，用字串操作來模擬乘法的步驟可以先實現字串高精度加法，再將加法運用到乘法過程中。這種方法簡單但是耗時比較大，這裡介紹一種比較巧妙的方法，借鑑LeetCode上的一份高票程式碼。

c++程式碼如下：

//高票程式碼版本
class Solution {
public:
    string multiply(string num1, string num2) {
        int m = num1.size();
        int
 
 n = num2.size();
        vector<int> array(m+n);
        string ans = "";
        for (int i = m-1; i >= 0; i--) {
            for (int j = n-1; j >= 0; j--) {
                int index1 = i + j;
                int index2 = i + j + 1;
                int sum = (num1[i]-'0')*(num2[j]-'0')+array
 
[index2];
                array[index1] += sum / 10;
                array[index2] = sum % 10;
            }
        }

        for (auto v:array) {
            if (ans.size() != 0 || v != 0)
                ans  += to_string(v);
        }

        return ans.size() == 0?"0":ans;
    }
};

//簡單但低效版本
class Solution {
public:
    string multiply(string num1, string num2) {
        if(num1.empty())
            return num2;
        if (num2.empty())
            return num1;
        if (num1.size() == 1 && num1[0] == '0')
            return "0";
        if (num2.size() == 1 && num2[0] == '0')
            return "0";

        string ans = "";
        int count = -1;
        for (int i = num1.size()-1;i >= 0; i--) {
            string tmp = "";
            int carry = 0;
            count++;
            for (int j = num2.size()-1; j >= 0; j--) {
                int m = (num1[i]-'0')*(num2[j]-'0')+carry;
                carry = m / 10;
                tmp = to_string(m%10)+tmp;
            }
            if (carry)
                tmp = to_string(carry)+tmp;
            int count_tmp = count;
            while (count_tmp) {
                tmp = tmp + "0";
                count_tmp--;
            }

            ans = add(ans,tmp);
        }
        return ans;
    }
    string add(string num1, string num2) {
        if(num1.empty())
            return num2;
        if (num2.empty())
            return num1;

        int carry = 0;
        int i = num1.size()-1;
        int j = num2.size()-1;
        string ans = "";

        while (i >= 0 && j >= 0) {
            int m = (num1[i]-'0')+(num2[j]-'0')+carry;
            carry = m / 10;
            ans = to_string(m%10) + ans;
            i--;
            j--;
        }
        while (i >= 0) {
            int m = (num1[i]-'0')+carry;
            carry = m / 10;
            ans = to_string(m%10) + ans;
            i--;
        }
        while (j >= 0) {
            int m = (num2[j]-'0')+carry;
            carry = m / 10;
            ans = to_string(m%10) + ans;
            j--;
        }
        if (carry)
            ans = to_string(carry)+ans;
        return ans;
    }
};