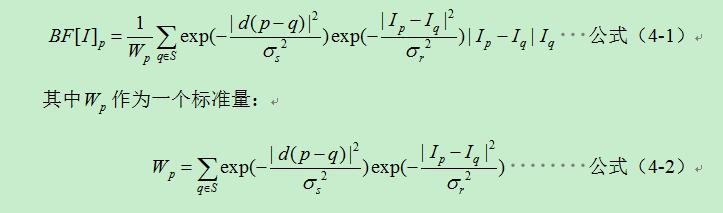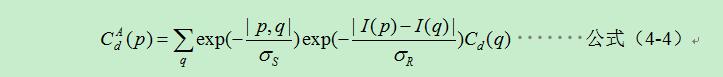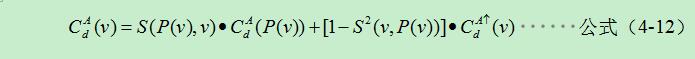圖割，置信傳播等全域性優化立體匹配演算法，由於運算過程中需要迭代求精，運算時間長，無法達到實時計算立體匹配的需求，然而實時性需求卻廣泛存在立體匹配的應用場景中。很多基於區域性匹配的演算法雖然運算時間短，但由於僅考慮匹配窗內的代價聚合，效果很差，視差圖只有很多稀疏的視差點，還要經過插值計算，顯然無法用於汽車導航，目標拾取等需要精確結果且對運算速度有一定要求的場景。

1區域性代價聚合

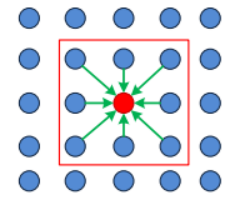
基於窗結構區域性立體匹配演算法，按照匹配約束來搜尋最佳的匹配點，在搜尋求取左右兩幅影象在視差d下一點的匹配代價時，實際是求得以該點為中心的匹配窗內所有點的代價的平均值（或者其他的度量方式）。如圖（4-1）：

圖 4-1 區域性匹配演算法的代價傳遞
Figure 4-1 Cost delivery of local aggregation
我們把這一過程叫做代價聚類（Cost aggregation），這種基於區域的匹配方法利用區域性視窗之間的相似性度量來匹配對應基元的空間座標，對於連續性細節明顯的區域效果較好。顯然，此類方法對於匹配窗以外的點卻無法影響該點的代價值，使得代價聚類的值不具有全域性特性，也就喪失了匹配基元的全域性結構特性，因此在紋理特徵較低的區域非常容易產生誤匹配。
如何在代價聚類中獲取匹配基元的全域性特徵，進而使得區域性代價聚合方法克服上述缺點，本章相對於基於區域的區域性窗立體匹配方法，採用圖論中的最小生成樹方法，利用樹結構進行全域性代價聚合。

2 雙邊濾波與代價聚合

雙邊濾波（Bilateral filter）是一種可以保邊去噪的濾波器。簡單的說就是一種同時考慮了畫素空間差異與強度差異的濾波器，因此具有保持影象邊緣的特性。該濾波器可以由兩個濾波引數進行控制。一個控制幾何空間距離。另一個控制畫素差。

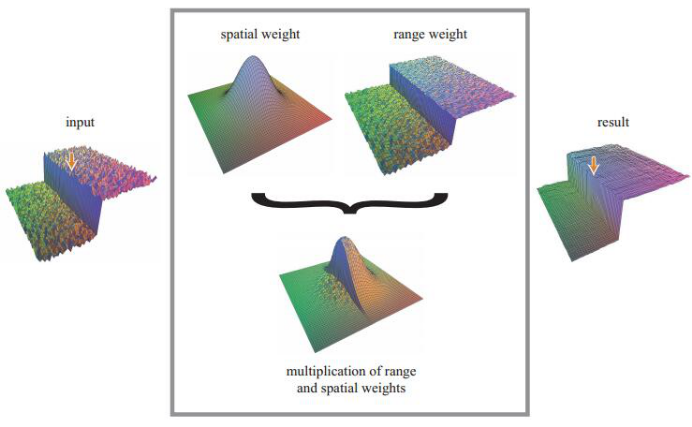
圖 4-2 雙邊濾波對空間和顏色權重的同時作用
Figure 4-2 bilateral filter weights of the central pixel
在傳統高斯濾波器中，權重只和畫素之間的空間距離有關係，無論影象的內容是什麼，都有相同的濾波效果。雙邊濾波器，在高斯濾波器的基礎上增加了畫素差值的權重資訊，公式（4-1）如下所示：

公式（4-1）是一個歸一加權平均，和分別衡量影象I的濾除量，前者控制距離資訊的權重，後者控制顏色資訊的權重。因此總體而言，在畫素強度變換不大的區域，雙邊濾波有類似於高斯濾波的效果，而在影象邊緣等強度梯度較大的地方，可以保持梯度。該特性在立體匹配問題中可以取代影象分割方法，或者作為影象分割方法的預處理手段，降低核心匹配演算法的計算量。
設為畫素p在視差層級d的匹配代價，為聚集代價。則雙邊濾波可以按照公式（4-1）與求取聚集代價進行融合中。

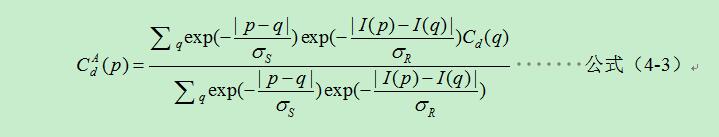
其中q作為支撐窗中的一個畫素。和與公式（4-1）的引數類似分別為調整空間相似性，和顏色（灰度）相似性的兩個引數。通常雙邊濾波函式計算中可以省去標準化的步驟，則公式（4-3）可以簡化為：

3 最小生成樹

最小生成樹也叫最小權重生成樹。在給定的無向圖中，(u,v)代表連線頂點u與頂點v的邊，w(u,v)代表此邊的權重，若存在T為E的子集且不存在環，使得w(T)最小，則T為G的最小生成樹。

根據最小生成樹結構，當把影象看做是一個四聯通區域的圖時，影象兩點所形成邊的權值定義為這兩點灰度值的差值（或者顏色資訊等其他度量準則），這種定義下生成的最小生成樹結構正好符合為匹配窗新增全域性特性的期望。

4 基於最小生成樹的代價聚合

求兩幅待匹配影象在視差d下一點的代價值時，基於區域的匹配窗代價聚合方法對與匹配窗以外的點無法影響該點的代價值，著眼於代價聚類，為了使代價值具有全域性屬性，使影象內所有點都對該點傳遞一個支撐量，距離該點較遠的顏色差別很大的畫素點傳遞較小的支撐量，距離相近顏色差別不大的傳遞較大的支撐量。
根據最小生成樹結構我們知道，當把影象看做是一個四聯通區域的圖時，影象兩點所形成邊的權值我們可以定義為這兩點灰度值的差值，這種定義下生成的MST結構正好符合我們的期望，相當於在區域性演算法上加了全域性性質，並且沒有增加過多的運算量。
基於最小生成樹的代價聚類過程十分簡單，針對待匹配影象生成一顆最小生成樹後，其代價聚合方式主要有兩種：
1.自底向上聚合，即從葉子節點到頂點的遍歷。
2.自頂向下聚合，即從頂點到葉子節點的遍歷。
對於每一個節點的聚合代價，只需要對生成樹遍歷兩次就可以得到結果（如圖4- ）。

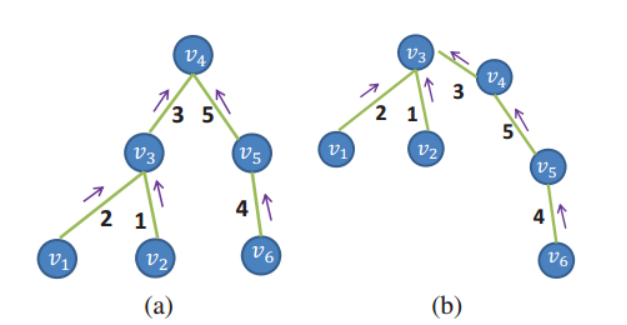
圖 4-3 兩種代價聚合方案
Firgure 4-3 Two cost aggregation schemes
設S（p，q）定義為兩點的相似度，D（p，q）定義為兩點的距離（MST兩點間的最小路徑），為聚類值。則有：

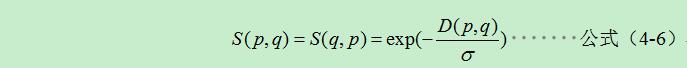
其中作為控制兩點之間相似度的引數。融合公式（4-4）雙邊濾波的結果後：

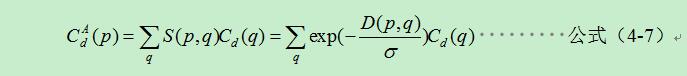
注意到公式（4-4）中存在兩個濾波控制引數，由於最小生成樹結構本身帶有距離度量，並且在樹中距離相近的畫素也越相似，所以公式（4-7）只使用一個引數控制相似度。
下面根據兩種聚合方式分別介紹如何計算聚合代價。

4.1 自底向上聚合（Leaf to Root）

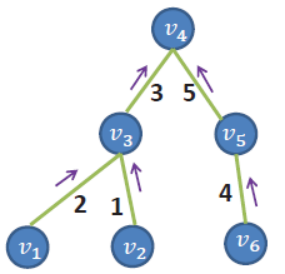
圖4-4 自底向上聚合
Figure 4-4 Leaf to Root aggregation
自底向上聚合即為Leaf to Root，是從葉子節點到根節點的代價聚合，以圖4-4為例，假設圖4-4是一個最小生成樹，邊上的數值代表權重，此時計算節點V4的代價聚合，那麼可以直接計運算元節點（V3， V4）的代價聚合值與各自邊緣的乘積集合，因為V4是根節點，不需要考慮父節點的影響。箭頭向上代表從葉子到當前節點的代價聚合值。則V4的聚合代價可以表示為公式（4-8）：

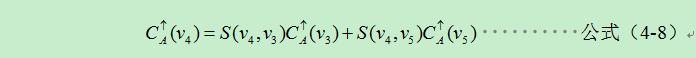
根據公式（4-8）可以推匯出計算自底向上聚合代價的方法，按照根節點的聚合代價為子節點聚合代價乘積的和來進行計算：

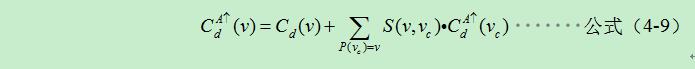
如果節點v是葉子節點，則
由於在計算過程中利用了最小生成樹的特性，自底向上的代價聚合過程中每一層的計算只需要計算其子節點的乘積，而子節點的代價聚合值已經包含了孫子節點及其子孫節點的影響。所以運算過程中極大的降低了運算量。

4.2 自頂向下聚合（Root to leaf）

對於圖4-4中的情況，V4沒有父親節點，屬於特殊情況，如果我們要計算V3的代價聚合值呢？顯然只考慮V1和V2是不夠的，還得考慮V4的影響。也就是從上到下的影響。如圖4-5所示：

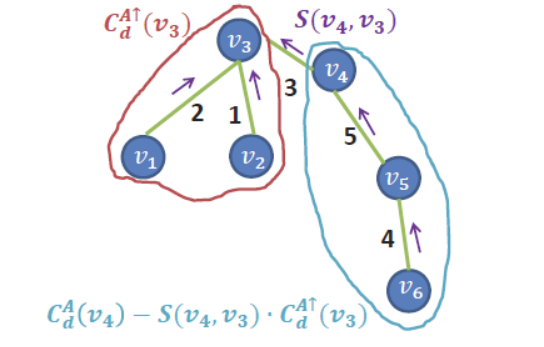
圖 4-5 自頂向下聚合
Figure 4-5 Root to leaf aggregation
此時我們完全可以假設V3為根節點，它的父節點向下轉換變為他的子節點，則可以利用同樣的辦法，將V4的代價聚合值乘以它的權重一起再加進來。但是因為V4的代價聚合值已經考慮到了V3的影響，所以必須事先將V4的代價聚合值減去V3的代價聚合值才可以。則V3的聚合代價值可以表示為：

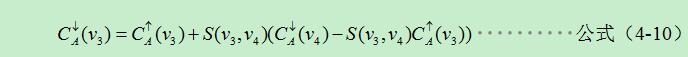
其中，自頂向下的代價聚合值就是最終的代價聚合值，要從上到下一層一層的計算代價，這樣同樣可以減少計算量。對於更為一般的情況，即當從根節點向葉子節點代價聚集時候，根據公式（4-10）可以推匯出其一般形式：

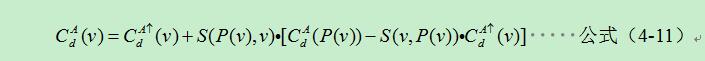
化簡得：

5 立體匹配的通用並行化處理

並行程式開發的程式設計模型主要分為兩類：1.訊息傳遞模型，2.共享儲存模型。本文主要採用共享儲存模型在彩色影象的各個通道上採取粗粒度的並行劃分，在彩色影象上進行並行化處理，各個通道內部針對濾波演算法，最小生成樹的建立等演算法，進行基於處理器指令向量化的SIMD擴充套件。
其主要流程如下流程圖所示：

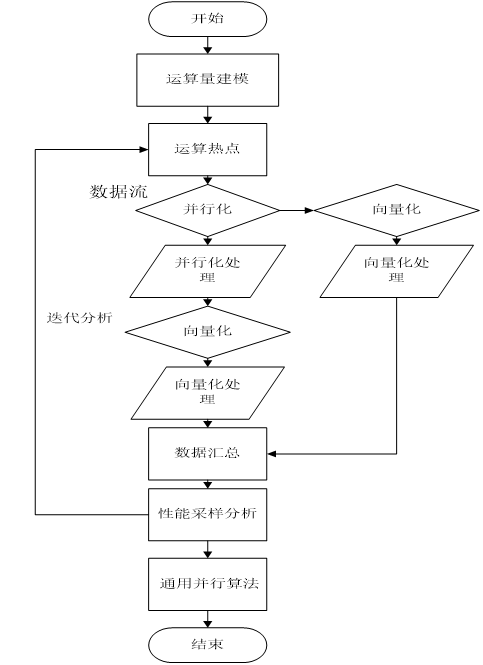
圖4- 並行化立體匹配流程
Figure 4-
首先針對基於最小生成樹的全域性立體匹配演算法，的整個演算法流程進行計算量分析建模，分析並提取其中的密集計算任務，參照[32]進行雙邊濾波的優化

5.1 OpenMP 執行緒並行化

OpenMP實際上是對共享記憶體並行系統，提供了一套指導性的編譯註釋方案。現在的常用的品牌基於x86架構的Intel AMD桌面處理器，基於ARM架構的處理器對OpenMP都有很好的支援。作為主流的共享記憶體模型，得到了幾乎所有商業編譯器的支援，具有很好的可移植性。
主要是，加上openmp程式碼編譯選項後，程式碼可移植了。

5.2 通用處理器指令優化（SIMD向量化計算）

幾乎所有的處理器廠商都為自己的處理器產品製作了多媒體擴充套件部件。圖形處理器的平行計算需要額外的硬體投入，而且與記憶體交換資料需要耗費時間。多媒體擴充套件部件一般在處理器中以向量部件的形式出現，相應的指令集以（Single Instruction Multi Data）單指令多資料流作為出現.
SIMD在效能上的優勢：編輯以加法指令為例，單指令單資料（SISD）的CPU對加法指令譯碼後，執行部件先訪問記憶體，取得第一個運算元；之後再一次訪問記憶體，取得第二個運算元；隨後才能進行求和運算。而在SIMD型的CPU中，指令譯碼後幾個執行部件同時訪問記憶體，一次性獲得所有運算元進行運算。這個特點使SIMD特別適合於多媒體應用等資料密集型運算。
SIMD適量指令能夠加速如C和Java語言的處理。向量指令對過個數據元素進行並行操作，從而使主機能夠快速處理大量資料。這對於社交媒體和大資料工作負載來說是個福音，但對面臨普通負載的系統程式設計師來說似乎沒有太大的幫助。
SIMD指令通過多種方式增加吞吐量。大多數機器指令會的結果會覆蓋輸入運算元其中之一不同，大部分SIMD指令集會使用兩個輸入暫存器，並將結果儲存在第三個暫存器。這意味著程式設計師可以節省與暫存器糾結的時間。
向量暫存器為128位元組長度。前16個暫存器實際上與64位浮點暫存器(FPRs)共存。改變一個FPR同樣會破壞對應向量暫存器的所有位元組。存在一些關於通過程式呼叫保護向量暫存器的特殊規則，IBM的Assembler Services Guide有詳細說明。
SIMD向量指令包括所有數學函式和浮點模式。同樣也有字串操作以及用於獲取和儲存資料的方法。

參考文獻

[11]Yang Q. A non-local cost aggregation method for stereo matching[C]// Proceedings / CVPR, IEEE Computer Society Conference on Computer Vision and Pattern Recognition. IEEE Computer Society Conference on Computer Vision and Pattern Recognition. 2012:1402-1409.
[12]Yang Q, Ji P, Li D, et al. Fast stereo matching using adaptive guided filtering[J]. Image and Vision Computing, 2014, 32(3): 202-211.
[13]Yang Q. Hardware-efficient bilateral filtering for stereo matching[J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 2014, 36(5): 1026-1032.
[14]Yang Q. Stereo Matching Using Tree Filtering[J]. Pattern Analysis & Machine Intelligence IEEE Transactions on, 2015, 37(4):834-846.

論文資源合集