December 16, 2015 12:01 PM

1.相關概念

1）生成樹 一個連通圖的生成樹是它的極小連通子圖，在n個頂點的情形下，有n-1條邊。生成樹是對連通圖而言的，是連同圖的極小連通子圖，包含圖中的所有頂點，有且僅有n-1條邊。非連通圖的生成樹則組成一個生成森林；若圖中有n個頂點，m個連通分量，則生成森林中有n-m條邊。

2）和樹的遍歷相似，若從圖中某頂點出發訪遍圖中每個頂點，且每個頂點僅訪問一次，此過程稱為圖的遍歷， (Traversing Graph)。圖的遍歷演算法是求解圖的連通性問題、拓撲排序和求關鍵路徑等演算法的基礎。圖的遍歷順序有兩種：深度優先搜尋（DFS）和廣度優先搜尋（BFS）。對每種搜尋順序，訪問各頂點的順序也不是唯一的。

3）在一個無向連通圖G中，其所有頂點和遍歷該圖經過的所有邊所構成的子圖G′ 稱做圖G的生成樹。一個圖可以有多個生成樹，從不同的頂點出發，採用不同的遍歷順序，遍歷時所經過的邊也就不同。

在圖論中，常常將樹定義為一個無迴路連通圖。對於一個帶權的無向連通圖，其每個生成樹所有邊上的權值之和可能不同，我們把所有邊上權值之和最小的生成樹稱為圖的最小生成樹。求圖的最小生成樹有很多實際應用。例如，通訊線路鋪設造價最優問題就是一個最小生成樹問題。
常見的求最小生成樹的方法有兩種：克魯斯卡爾(Kruskal)演算法和普里姆（Prim）演算法。

2.普里姆（Prim）演算法

1） 演算法的基本思想：

普里姆演算法的基本思想：普里姆演算法是另一種構造最小生成樹的演算法，它是按逐個將頂點連通的方式來構造最小生成樹的。

從連通網路 N = { V, E }中的某一頂點 u0 出發，選擇與它關聯的具有最小權值的邊(u0, v)，將其頂點加入到生成樹的頂點集合U中。以後每一步從一個頂點在U中，而另一個頂點不在U中的各條邊中選擇權值最小的邊(u, v),把該邊加入到生成樹的邊集TE中，把它的頂點加入到集合U中。如此重複執行，直到網路中的所有頂點都加入到生成樹頂點集合U中為止。

假設G=(V，E)是一個具有n個頂點的帶權無向連通圖，T(U，TE)是G的最小生成樹，其中U是T的頂點集，TE是T的邊集，則構造G的最小生成樹T的步驟如下：

（1）初始狀態，TE為空，U={v0}，v0∈V；

（2）在所有u∈U，v∈V-U的邊(u，v) ∈E中找一條代價最小的邊(u′，v′)併入TE，同時將v′併入U；

重複執行步驟（2）n-1次，直到U=V為止。

在普里姆演算法中，為了便於在集合U和(V-U)之間選取權值最小的邊，需要設定兩個輔助陣列closest和lowcost，分別用於存放頂點的序號和邊的權值。
對於每一個頂點v∈V-U，closest[v]為U中距離v最近的一個鄰接點，即邊 (v，closest[v]) 是在所有與頂點v相鄰、且其另一頂點j∈U的邊中具有最小權值的邊，其最小權值為lowcost[v]，即lowcost[v]=cost[v][closest[v]]，採用鄰接表作為儲存結構：

設定一個輔助陣列closedge[]：

lowcost域 存放生成樹頂點集合內頂點到生成樹外各頂點的各邊上的當前最小權值；

adjvex域 記錄生成樹頂點集合外各頂點距離集合內哪個頂點最近(即權值最小)。
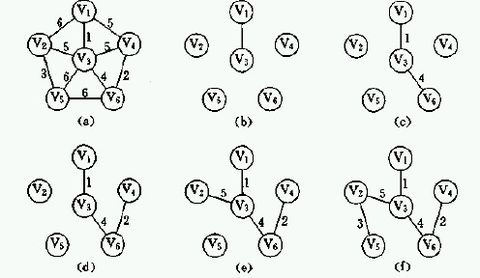
應用Prim演算法構造最小生成樹的過程:

#Prim.py
#王淵
#2015.12.16
#Email:[email protected]

from pylab import *
from mpl_toolkits.mplot3d import Axes3D

#Display the Chinese word
rcParams['font.sans-serif'] = ['SimHei']
rcParams['axes.unicode_minus'] = False

INFINITY = 65535                        #代表無窮大
vexs = array([[0,10,INFINITY,INFINITY,INFINITY,11,INFINITY,INFINITY,INFINITY],#鄰接矩陣
        [10,0,18,INFINITY,INFINITY,INFINITY,16,INFINITY,12],
        [INFINITY,INFINITY,0,22,INFINITY,INFINITY,INFINITY,INFINITY,8],
        [INFINITY,INFINITY,22,0,20,INFINITY,INFINITY,16,21],
        [INFINITY,INFINITY,INFINITY,20,0,26,INFINITY,7,INFINITY],
        [11,INFINITY,INFINITY,INFINITY,26,0,17,INFINITY,INFINITY],
        [INFINITY,16,INFINITY,INFINITY,INFINITY,17,0,19,INFINITY],
        [INFINITY,INFINITY,INFINITY,16,7,INFINITY,19,0,INFINITY],
        [INFINITY,12,8,21,INFINITY,INFINITY,INFINITY,INFINITY,0]])

lengthVex = len(vexs)                   #鄰接矩陣大小
adjvex = zeros(lengthVex)               #連通分量，初始只有第一個頂點，當全部元素為1後，說明連通分量已經包含所有頂點
adjvex[0] = 1;
lowCost = vexs[0,:]                     #記錄與連通分量連線的頂點的最小權值，初始化為與第一個頂點連線的頂點權值
lowCost[0] = 0
count = 0
while (count<9):
    I = (argsort(lowCost))[count]
    print("Vertex   [",count,"]:",I)
    adjvex[I] = lowCost[I]
    print("Edge [",count,"]:",adjvex[I])
    lowCost[I] = 0
    lowCost = array(list(map(lambda x,y:x if x<y else y,lowCost,vexs[I,:])))
    count = count+1
print("The length of the minimum cost spanning tree is: ", sum(adjvex))

執行結果：
Vertex代表依次加入最小生成樹的各頂點，Edge代表依次加入最小生成樹的各條邊，最後給出最小生成樹的總的長度。

Vertex  [ 0 ]: 0
Edge    [ 0 ]: 0.0
Vertex  [ 1 ]: 1
Edge    [ 1 ]: 10.0
Vertex  [ 2 ]: 5
Edge    [ 2 ]: 11.0
Vertex  [ 3 ]: 8
Edge    [ 3 ]: 12.0
Vertex  [ 4 ]: 2
Edge    [ 4 ]: 8.0
Vertex  [ 5 ]: 6
Edge    [ 5 ]: 16.0
Vertex  [ 6 ]: 7
Edge    [ 6 ]: 19.0
Vertex  [ 7 ]: 4
Edge    [ 7 ]: 7.0
Vertex  [ 8 ]: 3
Edge    [ 8 ]: 16.0
The length of the minimum cost spanning tree is:  99.0