今天想跟大家聊的，是我們經常用到，但是卻讓大家覺得十分神祕的那個演算法：A* 。

 

想必大家都玩兒過對戰類的遊戲，讀書那會兒，中午吃完飯就會跟幾個好哥們兒一起來兩局紅警。後來升級了，玩兒星際（是不是暴露年齡了，哈哈~~）。

玩兒的時候，就會發現這裡面的兵（為了方便描述，把坦克、飛艇、礦車等統稱為兵），你只要指定好地點，他們就會自己朝目的地進發，最終去向你指定的地點。不過紅警的實現似乎要差一點，經常走繞路，然後在路上就莫名其妙被人幹了……

於是，老王就對這個找路演算法做了些研究，去查了查資料。所有的資料都一致顯示，這些尋路演算法，基本上使用的都是一個叫做A*的演算法。不過當時看了演算法，沒有去實踐，所以也沒有太深入的思考，只是知道他是一種啟發式的搜尋演算法，能夠比較快的找到相對優的路徑。說來也巧，後來因為百度的A-Star演算法比賽進入百度實習，才瞭解了很多網際網路相關的技術。

說在前面的話：因為老王不是做遊戲的，遊戲的尋路演算法肯定有做各種優化，老王只是聊聊自己理解的A*演算法，所以講的不對的地方請專家們指正，專家們切勿生氣^_^

好了，背景說完了，我們開始吧~

廣度優先（BFS）和深度優先（DFS）搜尋

在談A*之前，還是要先聊聊搜尋演算法中的老祖宗，深度和廣度優先搜尋演算法。這兩個演算法，基本上各教科書都會有講解，各種面試基本上也都會面到。不過為了講清楚A*，我們還是先一起來看看他們吧。

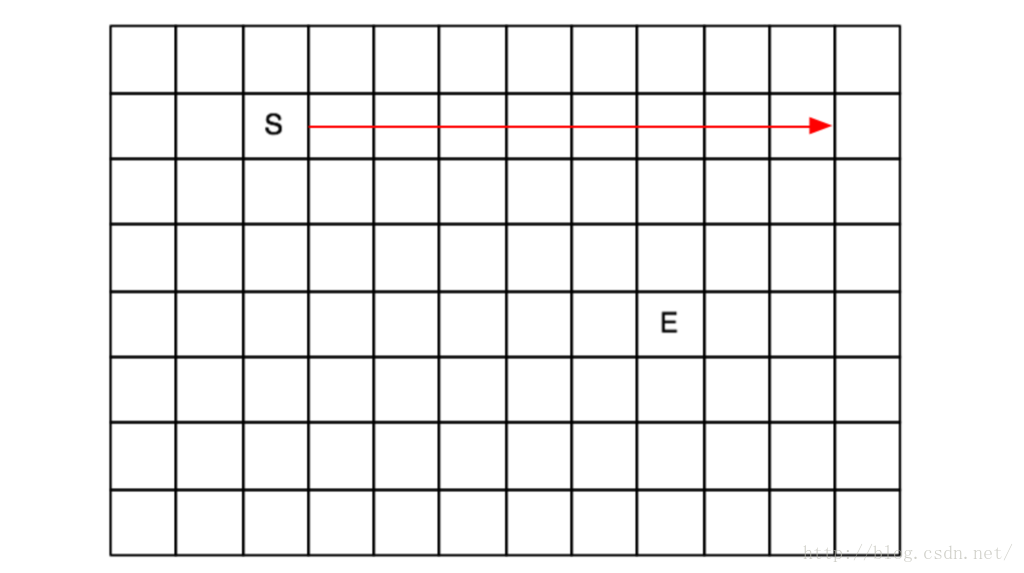
深度優先搜尋，用俗話說就是不見棺材不回頭。演算法會朝一個方向進發，直到遇到邊界或者障礙物，才回溯。一般在實現的時候，我們採用遞迴的方式來進行，也可以採用模擬壓棧的方式來實現。

如下圖，S代表起點，E代表終點。我們如果按照右、下、左、上這樣的擴充套件順序的話，演算法就會一直往右擴張，直到走到地圖的右邊界，發現沒找到目標點，然後再回溯。

這個演算法的好處就是實現簡單，可能就十幾行程式碼。不過問題也很明顯，就是：

1、路徑可能不是最優解；

2、尋路時間比較長。

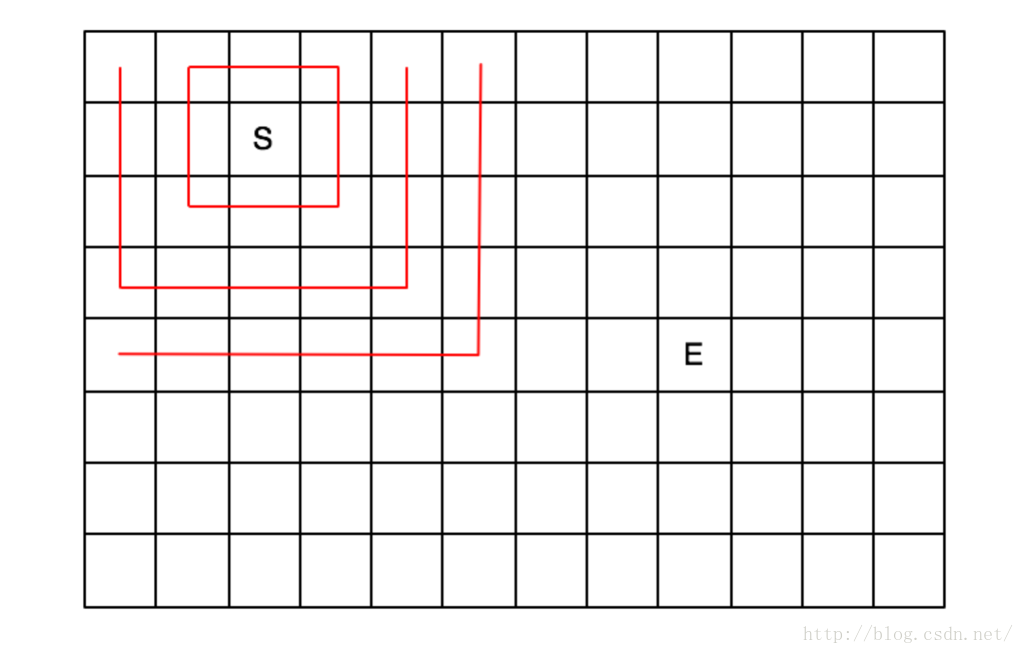
廣度優先搜尋，這個用形象的比喻，就像是地震波，從起點向外輻射，直到找到目標點。我們在實現的時候，一般採用佇列來實現。

這個演算法的優點：

1、簡單。程式碼也就幾十行；

2、路徑能找到最優解；

不足：

1、演算法消耗的時間比較大，遍歷的點會很多。

這裡就引出一個問題：為什麼廣度優先演算法能找到最優路徑，但是卻很耗時呢？

A*演算法

廣度優先搜尋之所以能找到最優的路徑，原因就是每一次擴充套件的點，都是距離出發點最近、步驟最少的。如此這樣遞推，當擴充套件到目標點的時候，也是距離出發點最近的。這樣的路徑自然形成了最短的路線。

任何事情都有正反兩面。正是由於廣度優先搜尋一層層的擴充套件，雖然讓他找到了最優的路線，但是，他卻很傻的走完了絕大多數格子，才找到我們的目標點。也就是，他只關注了當前擴充套件點和出發點的關係，而忽略了當前點和目標點的距離。如果，如果，如果……我們每擴充套件一個點，就踮起腳尖，看看詩和遠方，找找我們要尋找的那個目標，是不是就有可能指引我們快速的去往正確的方向，而不用傻乎乎的一層層的發展了呢？

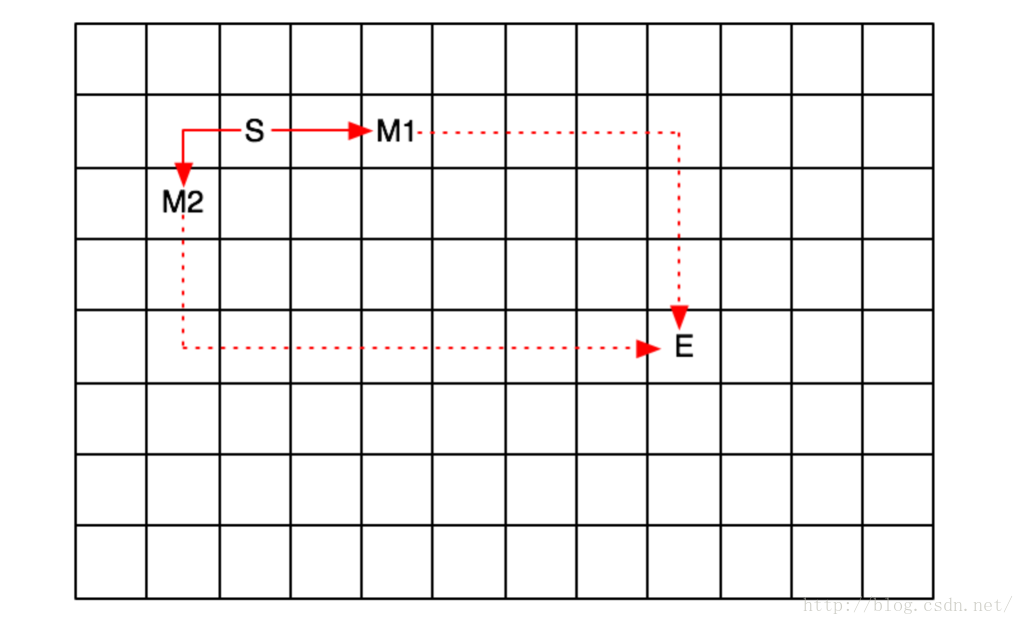
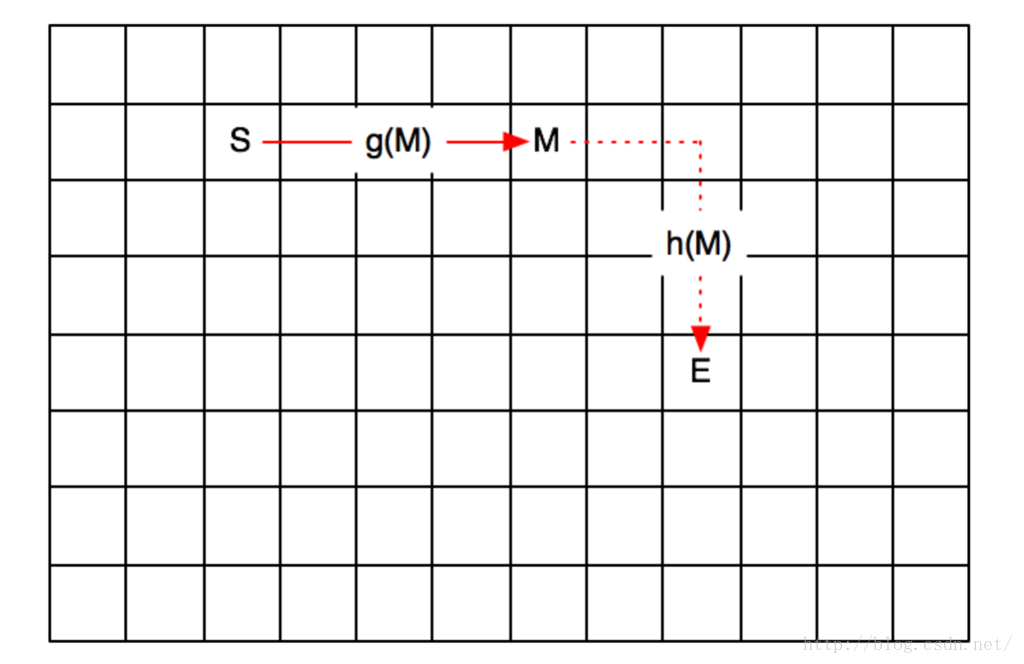
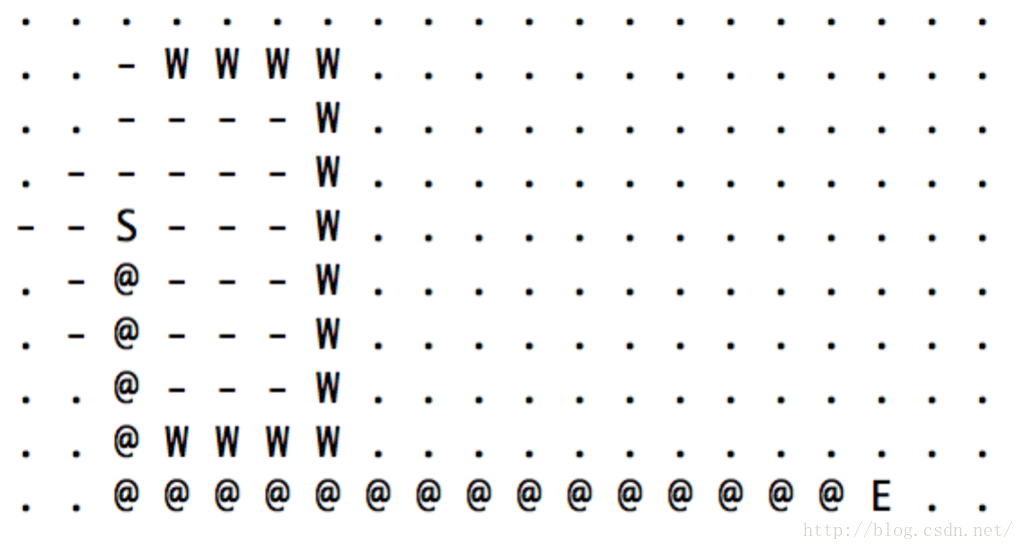
我們來看看下圖：

同樣是從出發點S走了兩步以後到達的M1和M2兩個點，如果讓你來選擇，你會選擇他們中的誰來做擴充套件點呢？很明顯，只要是眼力不差的人，都會選擇M1。為什麼呢？因為M2需要再走9步，才能到達終點E；而M1只需要7步！！！

注意了！我們的判斷依據，除了考慮了中間這個點同出發點的距離以外，還考慮了這個點同目標點的距離，對吧~

如果你想到了這一點，恭喜你，你已經掌握了A*演算法的祕訣了：A*演算法相對廣度優先搜尋演算法，除了考慮中間某個點同出發點的距離以外，還考慮了這個點同目標點的距離。這就是A*演算法比廣度優先演算法智慧的地方。也就是所謂的啟發式搜尋。

我們簡單的抽象一下，如果用f(M)表示：從起點S到終點E（經過M點）的距離，那他就可以表示成為兩段距離之和，即：S→M的距離 + M→E的距離。如果我們用符號表示的話，就可以寫成：f(M) = g(M) + h(M)。

怎麼樣，看起來這個公式是否是很簡單呢？

我們擴充套件到M點的時候，S→M的距離就已經知道，所以g(M)是已知的。但是M到E的距離我們還不知道。如果我們能用某種公式，能大概預測一下這個距離，而這個預測的值又比較精確，我們是不是就能很精確的知道每一個即將擴充套件的點是否是最優的解路徑上的點呢？這樣找起路來，是不是就很快呢？

所以，接下來最關鍵的問題，就是怎麼計算這個h(M)的值！

可能大家都會問一個問題：從M→E的距離不是很好計算嘛？用橫向的距離+縱向的距離就完了！

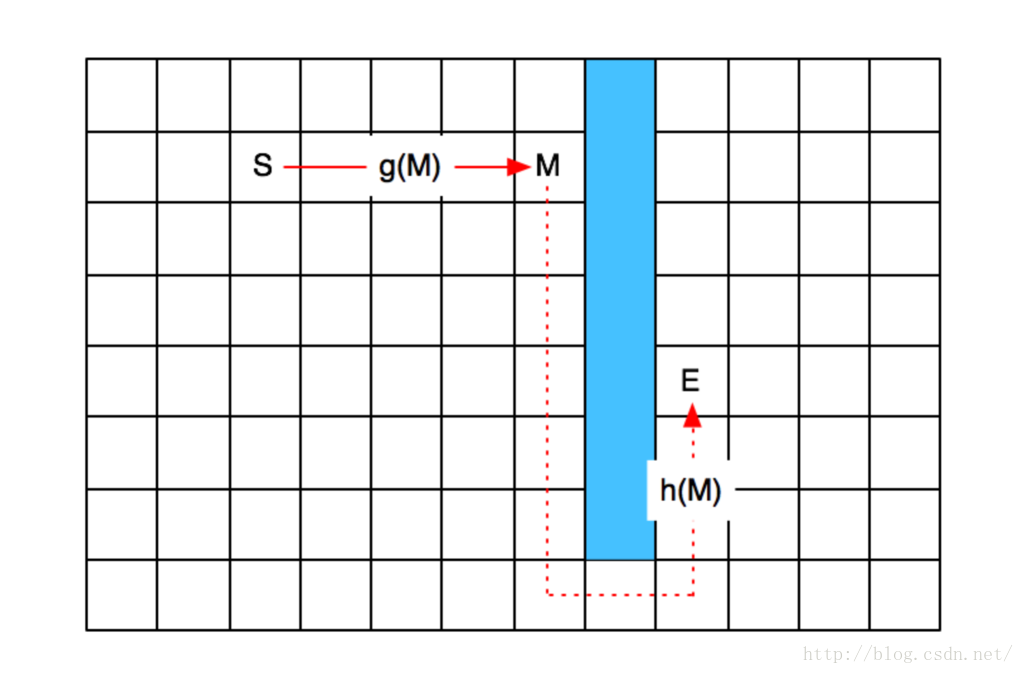
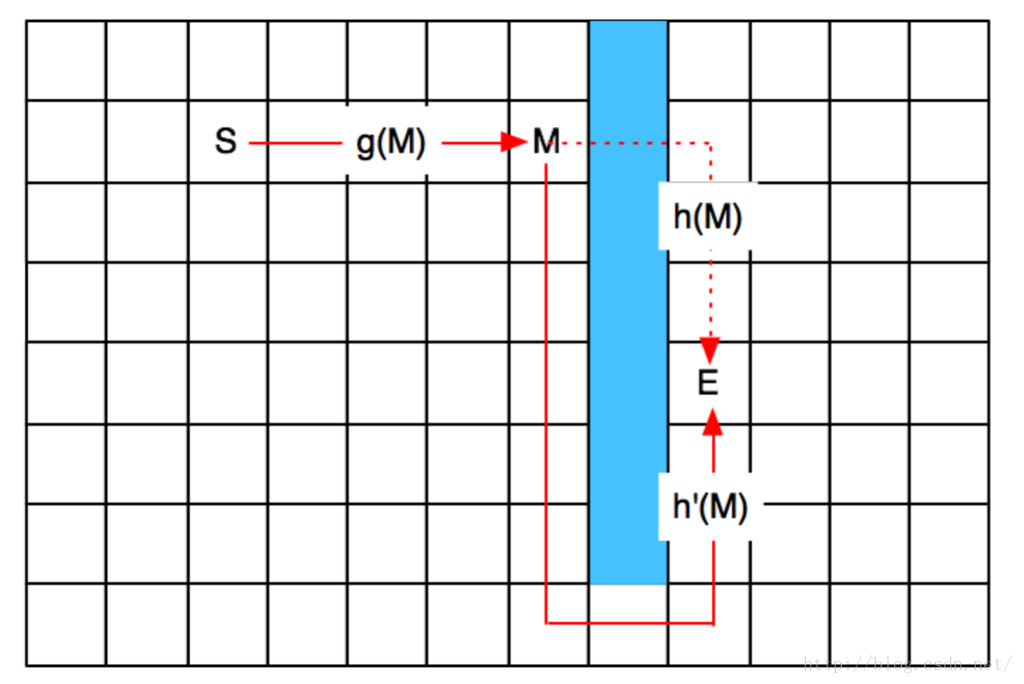
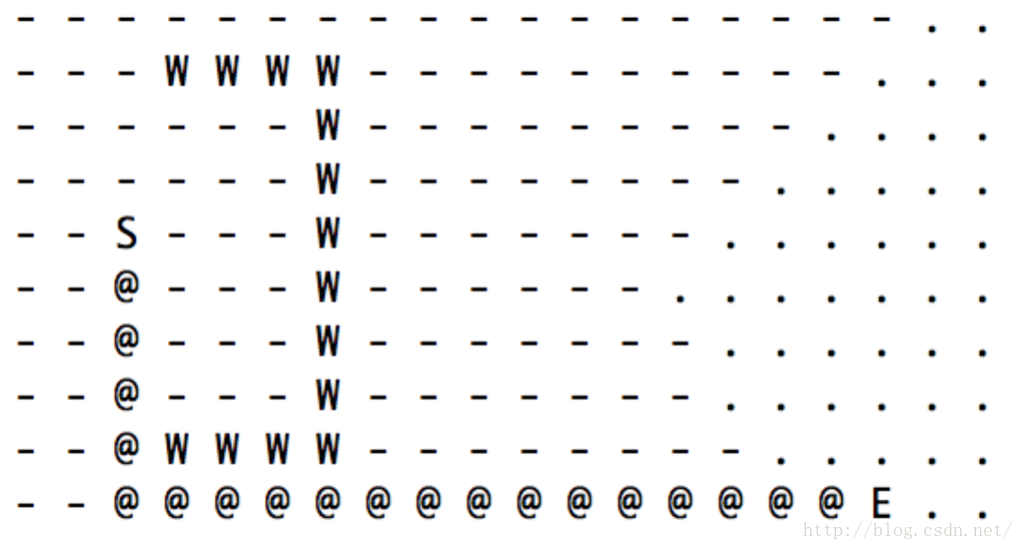
這個問題問的很好，但是結論是：既對，又不對。如果按照我們之前的圖來看，這個結論是正確的。但是，如果是下面這張圖呢？

在M和E之間，有一堵藍色的牆，這個時候，M→E的距離，還是橫向的直線距離 + 縱向的直線距離嘛？明顯不是了，他需要繞道！

這個時候，似乎希望破滅了……

前兩天有個朋友給我說，兩口子的相處之道，就是相互包容，不要太較真兒。如果我們將這個思想用到這裡，把h(M)看做一個估計的值，而不是精確值，那問題是不是就解決了呢？

也就是說，我們儘可能找那些f(M)=g(M)+h(M)小的點（其中h(M)是個估算值），當做我們的路徑經過點，即使實際的h'(M)值可能和h(M)值不等也沒關係，我們就當做一個參考（總比廣度優先搜尋好吧~）。如果通過這個估算，能幹掉很多明顯很差的點，我們也就節省了很多不必要的花銷，也算賺到了，對吧~

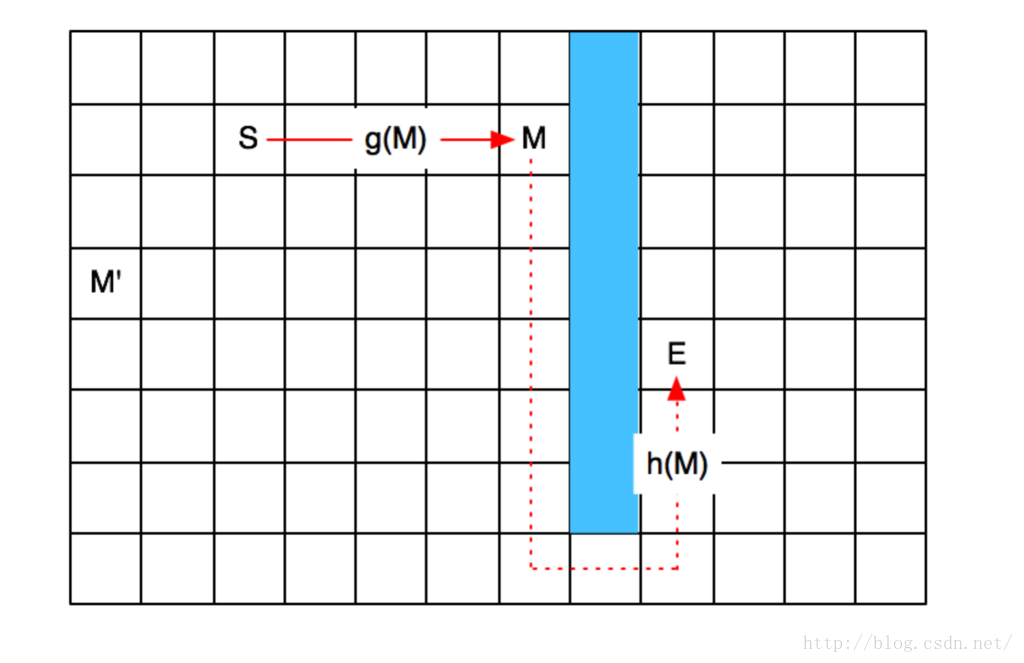
比如，上圖中， M點即使是繞路，也比M'點要強，對吧。在估算的時候，我們就可以將S左邊的點基本上都拋棄掉，從而減少我們擴充套件的點數，節約計算的時間。

說完上面的東東，我們大面兒上的東西就說的差不多了，接下來就省兩個問題要去解決了：

1、這個估算的函式h(M)怎麼樣去計算？

2、對於不同的估算函式h(M)來講，對於我們的搜尋結果會有什麼樣的影響？

那我麼一個個的來回答吧。

估算函式h(M)如何計算？

常見的距離計算公式有這麼幾種：

1、曼哈頓距離：這個名字聽起來好高階，說白了，就是上面我們講的橫向格子數+縱向格子數；

2、歐式距離：這個名字聽起來也很高階，說白了，就是兩點間的直線距離sqrt((x1-x2)2 + (y1-y2)2)

除了上述的距離計算公式以外，還有一些變種的距離計算公式，如：對角線距離等等。這個就在具體的問題中做具體的優化了。

不同估算函式對於結果的影響

那距離公式選擇不同，對我們的尋路結果有哪些影響呢？

1、當估算的距離h完全等於實際距離h'時，也就是每次擴充套件的那個點我們都準確的知道，如果選他以後，我們的路徑距離是多少，這樣我們就不用亂選了，每次都選最小的那個，一路下去，肯定就是最優的解，而且基本不用擴充套件其他的點。如下圖：

2、如果估算距離h小於實際距離h'時，我們到最後一定能找到一條最短路徑(如果存在另外一條更短的評估路徑，就會選擇更小的那個)，但是有可能會經過很多無效的點。極端情況，當h==0的時候，最終的距離函式就變成：

f(M)=g(M)+h(M)

=> f(M)=g(M)+0

=> f(M)=g(M)

這不就是我們的廣度優先搜尋演算法嘛？！ 他只考慮和起始點的距離關係，毫無啟發而言。

3、如果估算距離h大於實際距離h'時，有可能就很快找到一條通往目的地的路徑，但是卻不一定是最優的解。

因此，A*演算法最後留給我們的，就是在時間和距離上需要考慮的一個平衡。如果要求最短距離，則一定選擇h小於等於實際距離；如果不一定求解最優解，而是要速度快，則可以選擇h大於等於實際距離。

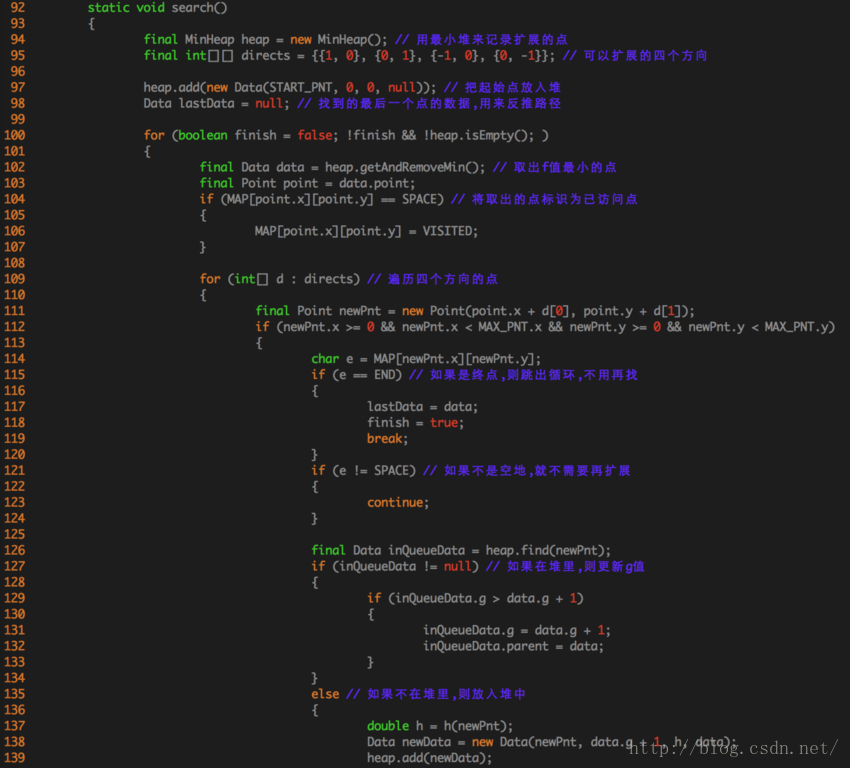
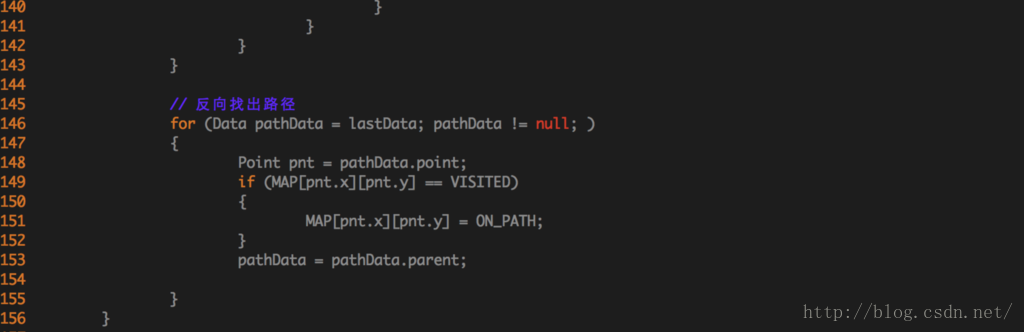
好了，口水話講了這麼多，來看程式碼吧。老王貼上了最核心的那段程式碼，如下：

完整的程式碼請參見老王的github：

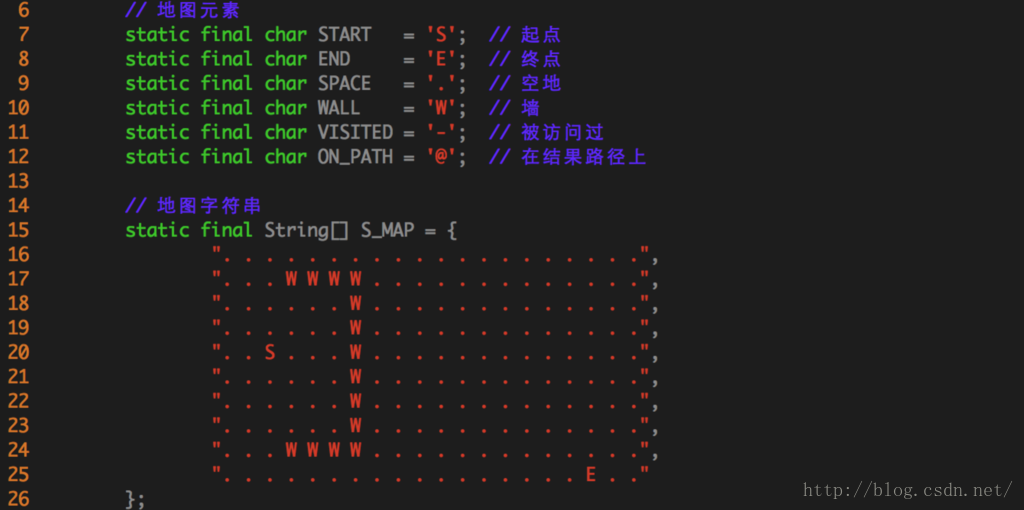
老王定義了一張地圖:

當用以下距離公式計算h值的時候，效果如圖：

1、曼哈頓距離：

很明顯，大部分的空白點都沒有去遍歷，而且最終找到了最優的路徑。

2、歐式距離：

同曼哈頓距離一樣，效果差不多，不過多擴充套件了幾個點。

3、歐式距離的平方

這種情況就是h值大於等於實際距離的，明顯他擴充套件的點很少，不過找到的路徑卻不是最短路徑。

4、BFS的情況（h值恆為0）

這種演算法基本等同於BFS，所有點基本都被擴充套件了，但是還是找到了最優的那個路徑。

好了，以上就是今天的內容，你看懂了嘛？如果覺得老王講的還有點意思，就請繼續關注老王的微信吧，每週固定時間，不見不散哦~

王哥的微信公眾號：                                                          

這裡還推薦一個微信公眾號，裡邊有許多程式設計師技術乾貨，

資源如下：

這是二維碼：