資料結構--棧和佇列的面試題
實現一個棧,要求實現Push(出棧)、Pop(入棧)、Min(返回最小值)的時間
複雜度為O(1)
方法1、棧Push時:當棧為空時,push兩次第一個資料。棧頂的數來儲存當前狀態的最小值。
再次Push資料時候,先拿將要Push的資料與棧頂的最小值進行比較,更新最小值。再將需要入棧的資料與最小一次入棧。
棧Pop:Pop兩次即可。
取最小值:返回棧頂資料。
方法2、用兩個棧,將資料與最小值分開存放在這兩個棧中。
優化前:棧Push
將資料Push進棧s1,每次比較完,將最小值push進s2裡。
棧Pop:分別Pop棧s1、s2。
優化後:棧Push
將資料Push進棧s1,每次比較完,如果將要入棧的資料比s2棧頂資料小的話,即將更新後的最小值push進s2棧裡邊。
棧Pop
Pop棧s1,如果s1棧頂資料與棧頂s2資料相等時候才Pop棧s2。
//方法2、優化後代碼實現:
//程式碼中用min代替了上述的s1,用data代替了s2
#ifndef test_h
#define test_h
#include"stack.h"
typedef struct MinStack
{
Stack _data;
Stack _min;
}MinStack;
void InitMinStack(MinStack*ms, size_t end);
void MinStackPush(MinStack*ms, SDataType x);
void MinStackPop(MinStack*ms);
SDataType Minstackmin(MinStack* #include"test.h"
#include"stack.h"
void MinStackTest()
{
MinStack s;
InitMinStack(&s,30);
MinStackPush(&s, 98);
MinStackPush(&s, 12);
MinStackPush(&s, 32);
MinStackPush(&s, 37);
MinStackPush(&s, 45);
while (MinStackEmpty(&s))
{
SDataType top = MinStackTop(&s);
SDataType min = Minstackmin(&s);
printf("top:%d min:%d\n ", top, min);
MinStackPop(&s);
}
}
使用兩個棧實現一個佇列
定義兩個佇列s1和s2。
入佇列:
直接Push到s1.
出佇列:
如果s2為空,s1不為空,把棧s1中的元素依次Pop掉,依次入棧到s2。否則直接Pop棧s2
//程式碼實現
typedef struct QueueByTwoStack{
Stack _s1;
Stack _s2;
}QueueByTwoStack;
void QueueByTwoStackInit(QueueByTwoStack*q);
void QueueByTwoStackPush(QueueByTwoStack*q, QDataType x);
void QueueByTwoStackPop(QueueByTwoStack*q);
int QueueByTwoStackEmpty(QueueByTwoStack*q);
QDataType QueueTwoStackFront(QueueByTwoStack*q);
void QueueByTwoStackInit(QueueByTwoStack*q)
{
assert(q);
StackInit(&(q->_s1), 10);
StackInit(&(q->_s2), 10);
}
void QueueByTwoStackPush(QueueByTwoStack*q,QDataType x)
{
assert(q);
StackPush(&(q->_s1), x);
}
void QueueByTwoStackPop(QueueByTwoStack*q)
{
if ((StackEmpty(&(q->_s2))) == 0){
while (StackEmpty(&(q->_s1))){
StackPush(&(q->_s2), StackTop(&(q->_s1)));
StackPop(&(q->_s1));
}
}
StackPop(&(q->_s2));
}
int QueueByTwoStackEmpty(QueueByTwoStack*q)
{
return StackEmpty(&(q->_s1)) + StackEmpty(&(q->_s2));
}
QDataType QueueTwoStackFront(QueueByTwoStack*q)
{
if (StackEmpty(&(q->_s2)) == 0)
{
while (StackEmpty(&(q->_s1)))
{
StackPush(&(q->_s2), StackTop(&(q->_s1)));
StackPop(&(q->_s1));
}
}
return StackTop(&(q->_s2));
}
void QueueByTwoStackTest()
{
QueueByTwoStack s;
QueueByTwoStackInit(&s);
QueueByTwoStackPush(&s, 1);
QueueByTwoStackPush(&s, 2);
QueueByTwoStackPush(&s, 3);
QueueByTwoStackPush(&s, 4);
QueueByTwoStackPush(&s, 5);
while (QueueByTwoStackEmpty(&s))
{
printf("%d ", QueueTwoStackFront(&s));
QueueByTwoStackPop(&s);
}
}
使用兩個佇列實現一個棧
該棧的Push功能:將陣列Push進佇列q1。
該棧的Pop功能:將佇列q1中的資料依次Pop到只留下隊尾結點。將q1中Pop出的資料依次Push到佇列q2中,將q1的隊尾結點Pop出去,即相當於將棧頂結點Pop。
typedef struct StackByTwoQueue{
Queue _q1;
Queue _q2;
}StackByTwoQueue;
void StackByTwoQueueInit(StackByTwoQueue*s);
void StackByTwoQueuePush(StackByTwoQueue*s,SDataType x);
void StackByTwoQueuePop(StackByTwoQueue*s);
SDataType StackByTwoQueueTop(StackByTwoQueue*s);
int StackByTwoQueueEmpty(StackByTwoQueue*s);
void StackByTwoQueueInit(StackByTwoQueue*s)
{
assert(s);
QueueInit(&(s->_q1));
QueueInit(&(s->_q2));
}
int StackByTwoQueueEmpty(StackByTwoQueue*s)
{
return QueueEmpty(&(s->_q1)) + QueueEmpty(&(s->_q2));
}
void StackByTwoQueuePush(StackByTwoQueue*s, SDataType x)
{
assert(s);
if (QueueEmpty(&(s->_q1)))
{
QueuePush(&(s->_q1), x);
}
else
{
QueuePush(&(s->_q2), x);
}
}
int SizeStackByQueue(StackByTwoQueue* s)
{
return QueueSize(&s->_q1) + QueueSize(&s->_q2);
}
void StackByTwoQueuePop(StackByTwoQueue*s)
{
assert(s);
if (QueueEmpty(&(s->_q1)))
{
while (QueueSize(&s->_q1)>1)
{
QueuePush(&(s->_q2), QueueFront(&(s->_q1)));
QueuePop(&(s->_q1));
}
QueuePop(&(s->_q1));
}
else
{
while (QueueSize(&s->_q2)>1)
{
QueuePush(&(s->_q1), QueueFront(&(s->_q2)));
QueuePop(&(s->_q2));
}
QueuePop(&(s->_q2));
}
}
SDataType StackByTwoQueueTop(StackByTwoQueue*s)
{
assert(s);
if (QueueEmpty(&(s->_q2)))
return QueueBack(&(s->_q2));
else
return QueueBack(&(s->_q1));
}
void TestStackByTwoQueue()
{
StackByTwoQueue s;
StackByTwoQueueInit(&s);
StackByTwoQueuePush(&s, 1);
StackByTwoQueuePush(&s, 2);
StackByTwoQueuePush(&s, 3);
StackByTwoQueuePush(&s, 4);
StackByTwoQueuePush(&s, 5);
printf("size = %d\n", SizeStackByQueue(&s));
printf("top = %d\n", StackByTwoQueueTop(&s));
while (StackByTwoQueueEmpty(&s)!=0)
{
printf("%d ", StackByTwoQueueTop(&s));
StackByTwoQueuePop(&s);
}
}
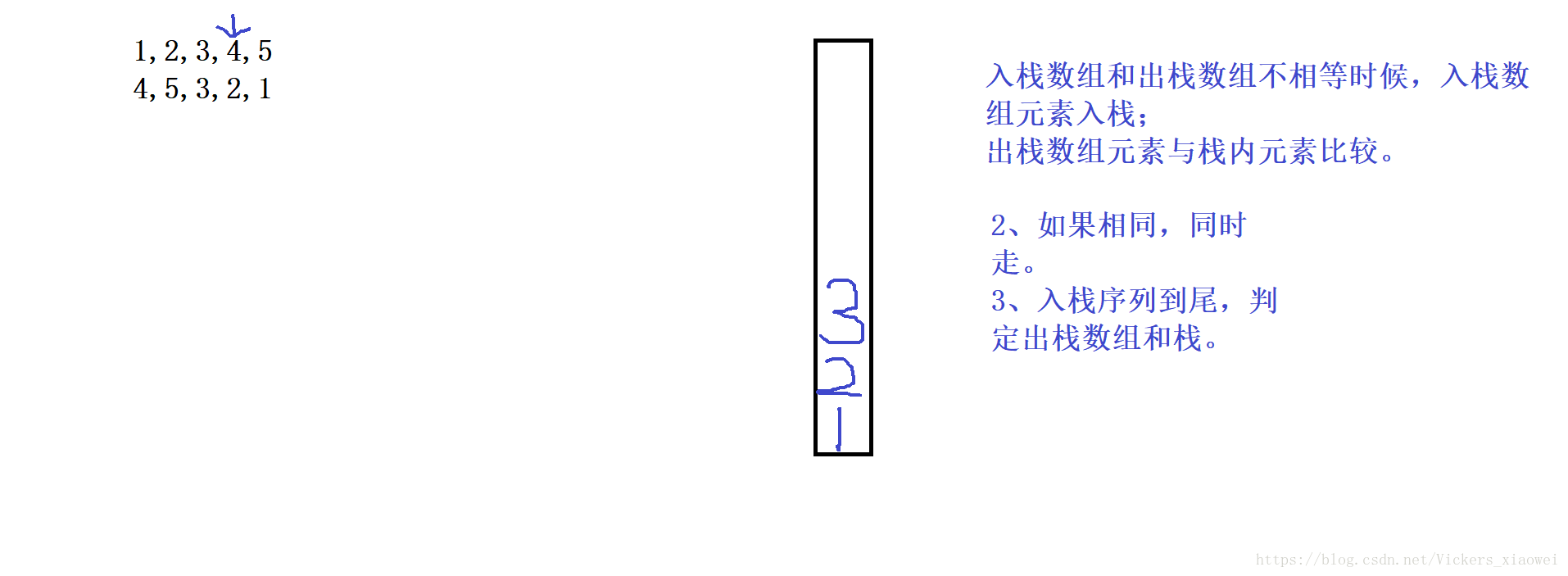
元素出棧、入棧順序的合法性。如入棧的序列(1,2,3,4,5),出棧序列為
(4,5,3,2,1)
定義入棧序列in[ ]={1,2,3,4,5};出棧序列out[ ]={4,5,3,2,1}
定義兩個變數index和outdex,用來分別表示in[ ]、out[ ]陣列的下標。
1、如果in[index]==out[outdex](說明in[index]是入棧後立即出棧),執行outdex++,index++,否則將in[index]依次Push進棧,index++。(in[index]入棧還在棧裡)
2、in[index]進棧又立即出棧之後,棧裡元素還有可能繼續出棧,所以需要判斷out[outindex]是否等於棧頂元素,如果是模擬這一過程。
當index走到頭後,判斷out[ ]陣列剩下的元素與棧內依次Pop的資料是否依次相等,如果是表明合法,返回0,否則返回-1。
int IsInvalidStackOrder(int* in, int* out, int n);
int IsInvalidStackOrder(int* in, int* out, int n)
{
int index = 0, outdex = 0;
Stack s;
StackInit(&s,30);
while (index < n)//先遍歷
{
if (in[index] != out[outdex])
{
StackPush(&s, in[index]);
index++;
}
else
{
//in[ ],與out[outdex]相等的,
//說明這個數入棧後,在下一個資料未入棧前就出棧了。
index++;
outdex++;
}
while (StackEmpty(&s) != 0&&StackTop(&s)==out[outdex])
//棧不為空,且棧頂與in[index]相等
//in[index]進棧又立即出棧之後,棧裡元素還有可能繼續出棧
{
outdex++;
StackPop(&s);
}
}
while (outdex < n)
{
if (StackTop(&s) != out[outdex])
return -1; //當出現棧頂元素與out[oudex]不能匹配,不合法
else
{
outdex++;
StackPop(&s);
}
}
return 0; //合法
}
void TestIsInvalidStackOrder()
{
int in[5] = { 1, 2, 3, 4, 5 };
int out[5] = { 4, 5, 3, 2, 1 };
printf("合法性:%d\n", IsInvalidStackOrder(in, out, sizeof(in) / sizeof(int)));
}
下面這是一個同學寫的有問題的程式碼:對比看看差別在哪裡??為什麼有問題呢??
int CheckInvaliOutStackOrder(int* a1,int* a2,int n)
{
int i = 0,index = 0, outdex = 0;
Stack s;
StackInit(&s);
while (i < n) {
if (a1[index] == a2[outdex])
{
++index;
++outdex;
}
else
{
StackPush(&s,a1[index]);
++index;
}
++i;
}
int j = outdex;
while(j < n){
if (StackTop(&s) == a2[outdex])
{
++outdex;
StackPop(&s);
}
else
return 0; //出棧序列不合適
++j;
}
return 1; //出戰序列合適
}
是的在in[index]進棧又立即出棧之後,棧裡元素還有可能繼續出棧,而該同學忘記了這一步的判斷。
一個數組實現兩個棧(共享棧)
前一個數組向後生長,後一個是陣列向前生長,用陣列操作模擬棧的作用。
typedef struct TwoStack{
SDataType* _a;
size_t _top1;
size_t _top2;
size_t _capacity;
}TwoStack;
void TwoStackInit(TwoStack* s, size_t capacity);
void TwoStackPush(TwoStack* s, SDataType x, int which