yolo v2之車牌檢測後續識別字符(二)
一、前言
這一篇續接前一篇《yolo v2之車牌檢測後續識別字符(一)》,主要是生成模型檔案、配置檔案以及訓練、測試模型。
二、python介面生成配置檔案、模型檔案
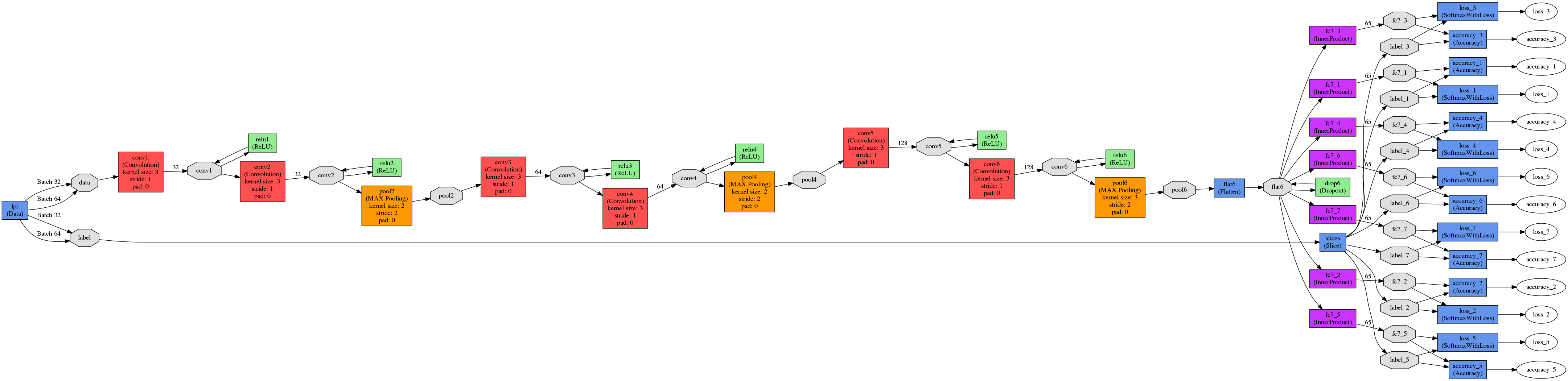
車牌圖片端到端識別的模型檔案參考自這裡,模型圖如下所示:
本來想使用caffe的python介面生成prototxt,結果發現很麻煩,容易出錯,直接在視覺化工具netscope上對已有prototxt做修改更方便,寫模型檔案時,注意輸入的圖片、卷積核大小、pad大小、stride大小、輸出圖片大小的關係,無論卷積層還是池化層,都有
輸入:n, c_i, h_i, w_i
輸出:n, c_o, h_o, w_o
滿足: h_o = ( h_i + 2*pad_h - kernel_h) / stride_h +1
w_o = ( w_i + 2*pad_w - kernel_w ) / stride_w +1
deploy檔案如下:#lpr_train_val.prototxt name: "Lpr" layer { name: "lpr" type: "Data" top: "data" top: "label" include { phase: TRAIN } transform_param { scale: 0.00390625 mean_file: "/home/jyang/caffe/LPR/Mean/mean.binaryproto" } data_param { source: "/home/jyang/caffe/LPR/Build_lmdb/train_lmdb" batch_size: 32 backend: LMDB } } layer { name: "lpr" type: "Data" top: "data" top: "label" include { phase: TEST } transform_param { scale: 0.00390625 mean_file: "/home/jyang/caffe/LPR/Mean/mean.binaryproto" } data_param { source: "/home/jyang/caffe/LPR/Build_lmdb/val_lmdb" batch_size: 32 backend: LMDB } } layer { name: "slices" type: "Slice" bottom: "label" top: "label_1" top: "label_2" top: "label_3" top: "label_4" top: "label_5" top: "label_6" top: "label_7" slice_param { axis: 1 slice_point: 1 slice_point: 2 slice_point: 3 slice_point: 4 slice_point: 5 slice_point: 6 } } layer { name: "conv1" type: "Convolution" bottom: "data" top: "conv1" param { lr_mult: 1 decay_mult: 1 } param { lr_mult: 2 decay_mult: 0 } convolution_param { num_output: 32 kernel_size: 3 stride: 1 weight_filler { type: "xavier" } bias_filler { type: "constant" } } } layer { name: "relu1" type: "ReLU" bottom: "conv1" top: "conv1" } layer { name: "conv2" type: "Convolution" bottom: "conv1" top: "conv2" param { lr_mult: 1 decay_mult: 1 } param { lr_mult: 2 decay_mult: 0 } convolution_param { num_output: 32 kernel_size: 3 stride: 1 weight_filler { type: "xavier" } bias_filler { type: "constant" } } } layer { name: "relu2" type: "ReLU" bottom: "conv2" top: "conv2" } layer { name: "pool2" type: "Pooling" bottom: "conv2" top: "pool2" pooling_param { pool: MAX kernel_size: 2 stride: 2 } } layer { name: "conv3" type: "Convolution" bottom: "pool2" top: "conv3" param { lr_mult: 1 decay_mult: 0 } param { lr_mult: 2 decay_mult: 0 } convolution_param { num_output: 64 kernel_size: 3 stride: 1 weight_filler { type: "xavier" } bias_filler { type: "constant" } } } layer { name: "relu3" type: "ReLU" bottom: "conv3" top: "conv3" } layer { name: "conv4" type: "Convolution" bottom: "conv3" top: "conv4" param { lr_mult: 1 decay_mult: 0 } param { lr_mult: 2 decay_mult: 0 } convolution_param { num_output: 64 kernel_size: 3 stride: 1 weight_filler { type: "xavier" } bias_filler { type: "constant" } } } layer { name: "relu4" type: "ReLU" bottom: "conv4" top: "conv4" } layer { name: "pool4" type: "Pooling" bottom: "conv4" top: "pool4" pooling_param { pool: MAX kernel_size: 2 stride: 2 } } layer { name: "conv5" type: "Convolution" bottom: "pool4" top: "conv5" param { lr_mult: 1 decay_mult: 0 } param { lr_mult: 2 decay_mult: 0 } convolution_param { num_output: 128 kernel_size: 3 stride: 1 weight_filler { type: "xavier" } bias_filler { type: "constant" } } } layer { name: "relu5" type: "ReLU" bottom: "conv5" top: "conv5" } layer { name: "conv6" type: "Convolution" bottom: "conv5" top: "conv6" param { lr_mult: 1 decay_mult: 0 } param { lr_mult: 2 decay_mult: 0 } convolution_param { num_output: 128 kernel_size: 3 stride: 1 weight_filler { type: "xavier" } bias_filler { type: "constant" } } } layer { name: "relu6" type: "ReLU" bottom: "conv6" top: "conv6" } layer { name: "pool6" type: "Pooling" bottom: "conv6" top: "pool6" pooling_param { pool: MAX kernel_size: 3 stride: 2 } } layer { name: "flat6" type: "Flatten" bottom: "pool6" top: "flat6" flatten_param { axis: 1 } } layer { name: "drop6" type: "Dropout" bottom: "flat6" top: "flat6" dropout_param { dropout_ratio: 0.5 } } layer { name: "fc7_1" type: "InnerProduct" bottom: "flat6" top: "fc7_1" param { lr_mult: 1 decay_mult: 0 } param { lr_mult: 2 decay_mult: 0 } inner_product_param { num_output: 65 weight_filler { type: "xavier" } bias_filler { type: "constant" } } } layer { name: "fc7_2" type: "InnerProduct" bottom: "flat6" top: "fc7_2" param { lr_mult: 1 decay_mult: 0 } param { lr_mult: 2 decay_mult: 0 } inner_product_param { num_output: 65 weight_filler { type: "xavier" } bias_filler { type: "constant" } } } layer { name: "fc7_3" type: "InnerProduct" bottom: "flat6" top: "fc7_3" param { lr_mult: 1 decay_mult: 0 } param { lr_mult: 2 decay_mult: 0 } inner_product_param { num_output: 65 weight_filler { type: "xavier" } bias_filler { type: "constant" } } } layer { name: "fc7_4" type: "InnerProduct" bottom: "flat6" top: "fc7_4" param { lr_mult: 1 decay_mult: 0 } param { lr_mult: 2 decay_mult: 0 } inner_product_param { num_output: 65 weight_filler { type: "xavier" } bias_filler { type: "constant" } } } layer { name: "fc7_5" type: "InnerProduct" bottom: "flat6" top: "fc7_5" param { lr_mult: 1 decay_mult: 0 } param { lr_mult: 2 decay_mult: 0 } inner_product_param { num_output: 65 weight_filler { type: "xavier" } bias_filler { type: "constant" } } } layer { name: "fc7_6" type: "InnerProduct" bottom: "flat6" top: "fc7_6" param { lr_mult: 1 decay_mult: 0 } param { lr_mult: 2 decay_mult: 0 } inner_product_param { num_output: 65 weight_filler { type: "xavier" } bias_filler { type: "constant" } } } layer { name: "fc7_7" type: "InnerProduct" bottom: "flat6" top: "fc7_7" param { lr_mult: 1 decay_mult: 0 } param { lr_mult: 2 decay_mult: 0 } inner_product_param { num_output: 65 weight_filler { type: "xavier" } bias_filler { type: "constant" } } } layer { name: "accuracy_1" type: "Accuracy" bottom: "fc7_1" bottom: "label_1" top: "accuracy_1" include { phase: TEST } } layer { name: "accuracy_2" type: "Accuracy" bottom: "fc7_2" bottom: "label_2" top: "accuracy_2" include { phase: TEST } } layer { name: "accuracy_3" type: "Accuracy" bottom: "fc7_3" bottom: "label_3" top: "accuracy_3" include { phase: TEST } } layer { name: "accuracy_4" type: "Accuracy" bottom: "fc7_4" bottom: "label_4" top: "accuracy_4" include { phase: TEST } } layer { name: "accuracy_5" type: "Accuracy" bottom: "fc7_5" bottom: "label_5" top: "accuracy_5" include { phase: TEST } } layer { name: "accuracy_6" type: "Accuracy" bottom: "fc7_6" bottom: "label_6" top: "accuracy_6" include { phase: TEST } } layer { name: "accuracy_7" type: "Accuracy" bottom: "fc7_7" bottom: "label_7" top: "accuracy_7" include { phase: TEST } } layer { name: "loss_1" type: "SoftmaxWithLoss" bottom: "fc7_1" bottom: "label_1" top: "loss_1" ###權重 loss_weight: 0.142857 # 1.0/7=0.142857 } layer { name: "loss_2" type: "SoftmaxWithLoss" bottom: "fc7_2" bottom: "label_2" top: "loss_2" ###權重 loss_weight: 0.142857 } layer { name: "loss_3" type: "SoftmaxWithLoss" bottom: "fc7_3" bottom: "label_3" top: "loss_3" ###權重 loss_weight: 0.142857 } layer { name: "loss_4" type: "SoftmaxWithLoss" bottom: "fc7_4" bottom: "label_4" top: "loss_4" ###權重 loss_weight: 0.142857 } layer { name: "loss_5" type: "SoftmaxWithLoss" bottom: "fc7_5" bottom: "label_5" top: "loss_5" ###權重 loss_weight: 0.142857 } layer { name: "loss_6" type: "SoftmaxWithLoss" bottom: "fc7_6" bottom: "label_6" top: "loss_6" ###權重 loss_weight: 0.142857 } layer { name: "loss_7" type: "SoftmaxWithLoss" bottom: "fc7_7" bottom: "label_7" top: "loss_7" ###權重 loss_weight: 0.142857 }
solver檔案如下:#lpr_deploy.prototxt name: "Lpr" layer { name: "data" type: "Input" top: "data" input_param { shape: { dim: 1 dim: 3 dim: 72 dim: 272 } } } layer { name: "conv1" type: "Convolution" bottom: "data" top: "conv1" param { lr_mult: 1 decay_mult: 1 } param { lr_mult: 2 decay_mult: 0 } convolution_param { num_output: 32 kernel_size: 3 stride: 1 weight_filler { type: "xavier" } bias_filler { type: "constant" } } } layer { name: "relu1" type: "ReLU" bottom: "conv1" top: "conv1" } layer { name: "conv2" type: "Convolution" bottom: "conv1" top: "conv2" param { lr_mult: 1 decay_mult: 1 } param { lr_mult: 2 decay_mult: 0 } convolution_param { num_output: 32 kernel_size: 3 stride: 1 weight_filler { type: "xavier" } bias_filler { type: "constant" } } } layer { name: "relu2" type: "ReLU" bottom: "conv2" top: "conv2" } layer { name: "pool2" type: "Pooling" bottom: "conv2" top: "pool2" pooling_param { pool: MAX kernel_size: 2 stride: 2 } } layer { name: "conv3" type: "Convolution" bottom: "pool2" top: "conv3" param { lr_mult: 1 decay_mult: 0 } param { lr_mult: 2 decay_mult: 0 } convolution_param { num_output: 64 kernel_size: 3 stride: 1 weight_filler { type: "xavier" } bias_filler { type: "constant" } } } layer { name: "relu3" type: "ReLU" bottom: "conv3" top: "conv3" } layer { name: "conv4" type: "Convolution" bottom: "conv3" top: "conv4" param { lr_mult: 1 decay_mult: 0 } param { lr_mult: 2 decay_mult: 0 } convolution_param { num_output: 64 kernel_size: 3 stride: 1 weight_filler { type: "xavier" } bias_filler { type: "constant" } } } layer { name: "relu4" type: "ReLU" bottom: "conv4" top: "conv4" } layer { name: "pool4" type: "Pooling" bottom: "conv4" top: "pool4" pooling_param { pool: MAX kernel_size: 2 stride: 2 } } layer { name: "conv5" type: "Convolution" bottom: "pool4" top: "conv5" param { lr_mult: 1 decay_mult: 0 } param { lr_mult: 2 decay_mult: 0 } convolution_param { num_output: 128 kernel_size: 3 stride: 1 weight_filler { type: "xavier" } bias_filler { type: "constant" } } } layer { name: "relu5" type: "ReLU" bottom: "conv5" top: "conv5" } layer { name: "conv6" type: "Convolution" bottom: "conv5" top: "conv6" param { lr_mult: 1 decay_mult: 0 } param { lr_mult: 2 decay_mult: 0 } convolution_param { num_output: 128 kernel_size: 3 stride: 1 weight_filler { type: "xavier" } bias_filler { type: "constant" } } } layer { name: "relu6" type: "ReLU" bottom: "conv6" top: "conv6" } layer { name: "pool6" type: "Pooling" bottom: "conv6" top: "pool6" pooling_param { pool: MAX kernel_size: 3 stride: 2 } } layer { name: "flat6" type: "Flatten" bottom: "pool6" top: "flat6" flatten_param { axis: 1 } } layer { name: "drop6" type: "Dropout" bottom: "flat6" top: "flat6" dropout_param { dropout_ratio: 0.5 } } layer { name: "fc7_1" type: "InnerProduct" bottom: "flat6" top: "fc7_1" param { lr_mult: 1 decay_mult: 0 } param { lr_mult: 2 decay_mult: 0 } inner_product_param { num_output: 65 weight_filler { type: "xavier" } bias_filler { type: "constant" } } } layer { name: "fc7_2" type: "InnerProduct" bottom: "flat6" top: "fc7_2" param { lr_mult: 1 decay_mult: 0 } param { lr_mult: 2 decay_mult: 0 } inner_product_param { num_output: 65 weight_filler { type: "xavier" } bias_filler { type: "constant" } } } layer { name: "fc7_3" type: "InnerProduct" bottom: "flat6" top: "fc7_3" param { lr_mult: 1 decay_mult: 0 } param { lr_mult: 2 decay_mult: 0 } inner_product_param { num_output: 65 weight_filler { type: "xavier" } bias_filler { type: "constant" } } } layer { name: "fc7_4" type: "InnerProduct" bottom: "flat6" top: "fc7_4" param { lr_mult: 1 decay_mult: 0 } param { lr_mult: 2 decay_mult: 0 } inner_product_param { num_output: 65 weight_filler { type: "xavier" } bias_filler { type: "constant" } } } layer { name: "fc7_5" type: "InnerProduct" bottom: "flat6" top: "fc7_5" param { lr_mult: 1 decay_mult: 0 } param { lr_mult: 2 decay_mult: 0 } inner_product_param { num_output: 65 weight_filler { type: "xavier" } bias_filler { type: "constant" } } } layer { name: "fc7_6" type: "InnerProduct" bottom: "flat6" top: "fc7_6" param { lr_mult: 1 decay_mult: 0 } param { lr_mult: 2 decay_mult: 0 } inner_product_param { num_output: 65 weight_filler { type: "xavier" } bias_filler { type: "constant" } } } layer { name: "fc7_7" type: "InnerProduct" bottom: "flat6" top: "fc7_7" param { lr_mult: 1 decay_mult: 0 } param { lr_mult: 2 decay_mult: 0 } inner_product_param { num_output: 65 weight_filler { type: "xavier" } bias_filler { type: "constant" } } } layer { name: "prob_1" type: "Softmax" bottom: "fc7_1" top: "prob_1" } layer { name: "prob_2" type: "Softmax" bottom: "fc7_2" top: "prob_2" } layer { name: "prob_3" type: "Softmax" bottom: "fc7_3" top: "prob_3" } layer { name: "prob_4" type: "Softmax" bottom: "fc7_4" top: "prob_4" } layer { name: "prob_5" type: "Softmax" bottom: "fc7_5" top: "prob_5" } layer { name: "prob_6" type: "Softmax" bottom: "fc7_6" top: "prob_6" } layer { name: "prob_7" type: "Softmax" bottom: "fc7_7" top: "prob_7" }
#My solver prototxt
net: "/home/jyang/caffe/LPR/Proto/lpr_train_val.prototxt"
test_iter: 338 #10815(張測試圖片)/32(batch_size) 取整得338
test_interval: 2236 #71547(張訓練圖片)/32(batch_size)取整得2236,即2236次迭代後開始一次測試
base_lr: 0.01
display: 100
max_iter: 111800 #50個epoch,50*2236=111800,最大迭代次數為111800
lr_policy: "step"
gamma: 0.1
stepsize: 8000
momentum: 0.9
weight_decay: 0.0005
snapshot: 20000 #20000次迭代儲存一次caffemodel
snapshot_prefix: "/home/jyang/caffe/LPR/lpr"
solver_mode: GPU
snapshot_format: BINARYPROTO這裡就不畫出loss函數了,在LPR資料夾下建立lpr_train.py。
#lpr_train.py
#!/usr/bin/env python
#coding=utf-8
import caffe
if __name__ =='__main__':
solver_file = '/home/jyang/caffe/LPR/Proto/lpr_solver.prototxt'
caffe.set_device(0) #select GPU-0
caffe.set_mode_gpu()
solver = caffe.SGDSolver(solver_file)
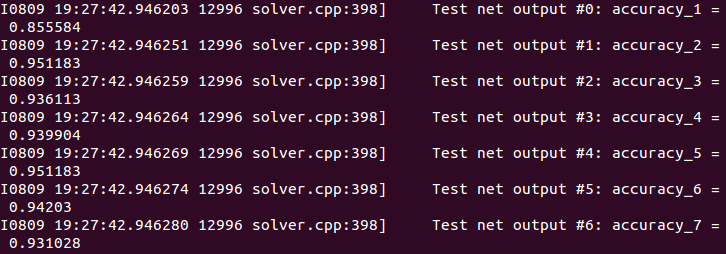
solver.solve()執行該 lpr_train.py 檔案,即開始訓練,可看到在驗證集上的準確率如下:
可看到第一個字元的識別率較為低,只有85%左右,其餘的均在93%以上
五、使用訓練得的模型做預測:
由於這裡用的是python 介面,故先將之前的均值檔案Mean.binaryproto 轉為 mean.npy ,在Mean資料夾下新建 binToNpy.py ,使用以下程式碼轉換
import numpy as np
import caffe
import sys
blob = caffe.proto.caffe_pb2.BlobProto()
data = open( 'mean.binaryproto' , 'rb' ).read()
blob.ParseFromString(data)
arr = np.array( caffe.io.blobproto_to_array(blob) )
out = arr[0]
np.save( 'mean.npy' , out )這樣deploy檔案、均值檔案、 caffemodel檔案準備好了,在LPR下建立 predict.py ,載入一張圖片作預測
#!/usr/bin/env python
#coding=utf-8
import cv2
import numpy as np
import sys,os
import time
import caffe
caffe_root = '/home/jyang/caffe/'
net_file = caffe_root + 'LPR/Proto/lpr_deploy.prototxt'
caffe_model = caffe_root + 'LPR/lpr_iter_40000.caffemodel'
mean_file = caffe_root + 'LPR/Mean/mean.npy'
img_path = caffe_root + 'LPR/001.png' #圖片路徑
labels = {0 :"京", 1 :"滬", 2 :"津", 3 :"渝",4 : "冀" , 5: "晉",6: "蒙", 7: "遼",8: "吉",9: "黑",10: "蘇",11: "浙",12: "皖",13:
"閩",14: "贛",15: "魯",16: "豫",17: "鄂",18: "湘",19: "粵",20: "桂", 21: "瓊",22: "川",23: "貴",24: "雲",
25: "藏",26: "陝",27: "甘",28: "青",29: "寧",30: "新",31: "0",32: "1",33: "2",34: "3",35: "4",36: "5",
37: "6",38: "7",39: "8",40: "9",41: "A",42: "B",43: "C",44: "D",45: "E",46: "F",47: "G",48: "H",
49: "J",50: "K",51: "L",52: "M",53: "N",54: "P",55: "Q",56: "R",57: "S",58: "T",59: "U",60: "V",
61: "W",62: "X",63: "Y",64: "Z" };
if __name__=='__main__':
net=caffe.Net(net_file,caffe_model,caffe.TEST)
transformer=caffe.io.Transformer({'data':net.blobs['data'].data.shape})
transformer.set_transpose('data' ,(2, 0, 1) )
#讀入的是H*W*C(0,1,2),但我們需要的是C*H*W(2,0,1 )
transformer.set_mean('data', np.load(mean_file).mean(1).mean(1) )
transformer.set_raw_scale('data' , 255)
#把資料從[0-1] rescale 至 [0-255]
transformer.set_channel_swap('data' ,(2 ,1 , 0))
#在caffe中讀入是BGR(0,1,2),所以要將RGB轉化為BGR(2,1,0)
start = time.time()
img=caffe.io.load_image(img_path )
img=img[...,::-1]
net.blobs['data'].data[...]=transformer.preprocess('data' , img)
out=net.forward()
prob=('prob_1','prob_2','prob_3','prob_4','prob_5','prob_6','prob_7')
for k in range(7):
index = net.blobs[prob[k]].data[0].flatten().argsort()[-1:-6:-1]
print labels[index[0]],
print("\nDone in %.2f s." % (time.time()-start ))
cv2.imshow( 'demo',img)
cv2.waitKey(0)


結語
實際測試圖片,發現完全正確識別的準確率很低,雖然訓練得到的模型在驗證集上的識別準確率很高,但是訓練集和驗證集都是經過樣本增強得到的,3922張擴充至80000多張,擴充的樣本和真實樣本還是存在差距,且即是擴充再多,樣本資訊還是有限的,導致過擬和了,如果能獲得幾萬張真實的車牌圖片,所訓練出的模型實用性將會更高。
相關推薦
yolo v2之車牌檢測後續識別字符(二)
一、前言 這一篇續接前一篇《yolo v2之車牌檢測後續識別字符(一)》,主要是生成模型檔案、配置檔案以及訓練、測試模型。 二、python介面生成配置檔案、模型檔案 車牌圖片端到端識別的模型檔案參考自這裡,模型圖如下所示: 本
yolo v2之車牌檢測後續識別字符(一)
一、前言 本篇續接前一篇 yolo v2 之車牌檢測 ,前一篇使用yolo v2已經可以很準確地框出車牌圖片了,這裡完成後續的車牌字元號碼的識別,從車牌框框中要識別出車牌字元,筆者能想到3種思路,1種是同樣yolo、SSD等深度學習目標檢測的方法直接對車牌內的
yolo v2 之車牌檢測
一、前言 二、準備工作 首先需要下載正確配置好darknet, 使用./darknet detect cfg/yolo.cfg yolo.weights data/dog.jpg 命令可得檢測結果。本文主要是為了檢測車牌區域,在darknet下新建一資料夾
基於OpenCV3.0的車牌識別系統設計(二)--車牌提取
寫在前面的話 上一篇開篇博文寫好之後找女朋友看了一下,希望她提一點建設性建議。結果她很委婉的告訴我,寫的還行就是太表面了,告訴我要注意細節的描述與具體的實現過程與原理等等。其實我只是想騙她看一下增加一下點選量,順便知道我寫的部落格新手能不能看懂而已。結果她告訴我,她那麼聰明當然能看懂,別人就
linux設備驅動之misc驅動框架源碼分析(二)
linux驅動開發misc設備驅動1、misc_open函數分析 該函數在driver/char/misc.c中,misc.c是驅動框架實現的,這裏面的misc_Open函數是misc驅動框架為應用層提供的一個打開misc設備的一個接口。 1、首先我們要知道在misc.c中的misc_init函數
HBase源代碼分析之HRegion上MemStore的flsuh流程(二)
初始化 back represent 代碼分析 讀數 ott pass expect 出現異常 繼上篇《HBase源代碼分析之HRegion上MemStore的flsuh流程(一)》之後。我們繼續分析下HRegion上MemStore flush的核心方
netty源碼分析之揭開reactor線程的面紗(二)
研究 tle 一段 issue 一段時間 [] iter cts ova 如果你對netty的reactor線程不了解,建議先看下上一篇文章netty源碼分析之揭開reactor線程的面紗(一),這裏再把reactor中的三個步驟的圖貼一下reactor線程我們已經了解到n
DBA成長之路---mysql數據庫服務(二)
連接查詢 過程 where 存在 arc nat 唯一索引 rest nal 管理表記錄 增加insert into 庫.表 values(字段值列表);insert into 庫.表(字段值列表) values(字段值列表);insert into 庫.表 values(
字符(串)讀寫
target null feo uva tchar spa ret ufs 一個 UVa 272,Tex Quotes: 輸入一段話,將引號由" ‘‘換成`` ‘‘輸出。 fgetc(fin); getchar(); fgets(buf,maxn,fin); 從打開
生物特征識別:小面積指紋識別算法(二)
dpi 如果 mage 卷積 噪聲 狀態 AMM 計算 log 算法(一)已經介紹了一種小面積指紋識別算法可選的方案,是一種經典的方案,對於面積足夠大且level2特征高於最小限制時,為一種低內存占用,快速的實現方法。但在某些應用場中中(比如終端中,要求占用面積較小,且面
Pthon學習之路 第四篇 Python基礎(二)
pri bsp programs -s alt 如果 lex class 算數運算 1.運算符:+ - *(乘法) /(除法) %(求余) //(求商) **(求冪) 2.成員運算:in not in:判斷單個字符或者子序列在不在字符串中。(n
zigbee 之ZStack-2.5.1a原始碼分析(二) 無線接收控制LED
本文描述ZStack-2.5.1a 模板及無線接收移植相關內容。 main HAL_BOARD_INIT // HAL_TURN_OFF_LED1 InitBoard HalDriverInit HalAdcInit
語音識別學習筆記(二)【基於向量量化的識別技術】
語音識別學習筆記(二)【基於向量量化的識別技術】 概述 量化分為標量量化和向量量化(Vector Quantization,VQ)。標量量化是將取樣後的訊號值逐個進行量化,而適量量化是將若干個取樣訊號分成一組,即構成一個向量,然後對此向量一次進行量化。向量量化
哈爾濱工業大學計算機學院-模式識別-課程總結(二)-概率密度函式的引數估計
1. 概率密度函式的引數估計 前文講到了利用貝葉斯決策理論構建貝葉斯分類器,初學者難免會有疑問,既然已經可以通過構建貝葉斯分類器的方法處理分類問題,那為什麼還要學習本章節內容? 事實上,貝葉斯分類器的缺可以通過計算先驗概率與類條件概率來設計最優分類器。但是對於大多數實際問題,我們往往無法知道這兩個
哈爾濱工業大學計算機學院-模式識別-課程總結(二)-概率密度函數的參數估計
展開 處理 play bold 避免 dot max 應用 既然 1. 概率密度函數的參數估計 前文講到了利用貝葉斯決策理論構建貝葉斯分類器,初學者難免會有疑問,既然已經可以通過構建貝葉斯分類器的方法處理分類問題,那為什麽還要學習本章節內容? 事實上,貝葉斯分類器的缺可以
linux一切皆檔案之Unix domain socket描述符(二)
一、知識準備 1、在linux中,一切皆為檔案,所有不同種類的型別都被抽象成檔案(比如:塊裝置,socket套接字,pipe佇列) 2、操作這些不同的型別就像操作檔案一樣,比如增刪改查等 3、主要用於:執行在同一臺機器上的2個程序相互之間的資料通訊 4、它們和網路檔案描述符非常相似(比如:TCP
將一個字符(char)或者一個整形(int)的二進制形式輸出
正序 inpu %d arr pre return char NPU 余數 要輸出一個數的二進制形式使用位操作 >> 和 & void putBinary(int number)//將一個int整形數字的二進制形式正序,倒序輸出 { int
ARM+Movidius VPU 目標識別除錯筆記(二)
演算法載入 在ARM+Movidius VPU 目標識別除錯筆記(一)一文中,我們通過對Ncsdk的分析,已經成功搭建了其開發環境,並且能成功執行簡單的HelloWorld程式了。 那麼我們下一步工作就是要分析清楚Ncsdk是如果操作來實現演算法加速的。
基於KNN分類演算法手寫數字識別的實現(二)——構建KD樹
上一篇已經簡單粗暴的建立了一個KNN模型對手寫圖片進行了識別,所以本篇文章採用構造KD樹的方法實現手寫數字的識別。 (一)構造KD樹 構造KD樹的基本原理網上都有介紹,所以廢話不多說,直接上程式碼。 #Knn KD_Tree演算法 import math from
Tensorflow1.8用keras實現MNIST資料集手寫字型識別例程(二)
class CNN(tf.keras.Model): def __init__(self): super().__init__() self.conv1 = tf.keras.layers.Conv2D( f