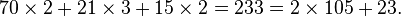POJ 1006 中國剩餘定理
初見poj1006用的暴力破解寫的程式碼,寫完以後發現很搓。上網一查原來古人早就對此類問題有了解答規則。
一、中國剩餘定理
一元線性同餘方程組問題最早可見於中國南北朝時期(公元5世紀)的數學著作《孫子算經》卷下第二十六題,叫做“物不知數”問題,原文如下:
有物不知其數,三三數之剩二,五五數之剩三,七七數之剩二。問物幾何?
即,一個整數除以三餘二,除以五餘三,除以七餘二,求這個整數。《孫子算經》中首次提到了同餘方程組問題,以及以上具體問題的解法,因此在中文數學文獻中也會將中國剩餘定理稱為孫子定理。
宋朝數學家秦九韶於1247年《數書九章》卷一、二《大衍類》對“物不知數”問題做出了完整系統的解答。明朝數學家
三人同行七十希,五樹梅花廿一支,七子團圓正半月,除百零五使得知
這個歌訣給出了模數為3、5、7時候的同餘方程的秦九韶解法。意思是:將除以3得到的餘數乘以70,將除以5得到的餘數乘以21,將除以7得到的餘數乘以15,全部加起來後除以105,得到的餘數就是答案。比如說在以上的物不知數問題裡面,使用以上的方法計算就得到
因此按歌訣求出的結果就是23.
大致過程是:
n1*5*7%3=1,則n1最小為2;2*5*7=70.
n2*3*7%5=1,則n2最小為1;1*3*7=21.
n3*5*3%7=1,則n3最小為1;1*3*5=15.
n%3=2;
n%5=3;
n%7=2;
所以n=(70*2+21*3+15*2)%(3*5*7)=233%105=23.
二、求解
有了上邊的演算法,求解poj1006就很簡單啦。由題意我們很容易得到:
(n+d)%23=p;
(n+d)%28=e;
(n+d)%33=i;
並且,若a%b=c, k為正整數,則k*a%b=(k*c)%b
33*28%23=4,則6*33*28%23=4*6%23=1; 6*33*28=5544
23*33%28=3,則19*23*33%28=19*3%28=1; 19*23*33=14421
28*23%33=17,則2*28*23%33=2*17%33=1; 2*28*23=1288
23、28、33互質,最小公倍數23*28*33=21252
(5544*p+14421*e+1288*i)%21252=n+d
程式碼如下:
#include "stdafx.h"
#include<iostream>
using namespace std;
int _tmain(int argc, _TCHAR* argv[])
{
int p,e,i,d;
cin>>p>>e>>i>>d;
int num=0;
int arr[10000][4];//用二維陣列儲存輸入
while(!(p==-1&&e==-1&&i==-1&&d==-1)){
arr[num][0]=p;
arr[num][1]=e;
arr[num][2]=i;
arr[num][3]=d;
num++;//num記錄輸入資料的組數
cin>>p>>e>>i>>d;
}
for(int i=0;i<num;i++){
int j=(5544*arr[i][0]+14421*arr[i][1]+1288*arr[i][2])%21252-arr[i][3];
if(j<=0)//防止出現輸出0或者負數的情況
j+=21252;
cout<<"Case "<<i+1<<": the next triple peak occurs in "<<j<<" days."<<endl;
}
return 0;
}
相關推薦
Biorhythms POJ - 1006 (中國剩餘定理)
傳送門 題意:已知一個人的身體,智力和情感的迴圈週期,然後給出一個人身體,智力和情感的開始值,最後再給出一個固定時間,問在下一次三個共同達到峰值的時間在這個固定時間多長時間後。 題解:中國剩餘定理板題,首先得了解拓展gcd,知道了這個後,再瞭解下求逆元傳送門,在看下百科上的解釋就懂了傳送門,
POJ 1006 中國剩餘定理
初見poj1006用的暴力破解寫的程式碼,寫完以後發現很搓。上網一查原來古人早就對此類問題有了解答規則。 一、中國剩餘定理 一元線性同餘方程組問題最早可見於中國南北朝時期(公元5世紀)的數學著作《孫子算經》卷下第二十六題,叫做“物不知數”問題,原文如下: 有物不知其數
POJ 1006: 中國剩餘定理
問題描述 人自出生起就有體力,情感和智力三個生理週期,分別為23,28和33天。一個週期內有一天為峰值,在這一天,人在對應的方面(體力,情感或智力)表現最好。通常這三個週期的峰值不會是同一天。現在給出三個日期,分別對應於體力,情感,智力出現峰值的日期。然後再
poj 1006中國剩餘定理的應用
這道題主要講的是人有是哪個生理週期,分別是身體,情感和智力,這三個週期,他們的為其時間是23,28和33.已經知道這一年裡從第一天開始第一個生理週期出現的時間分別是P,e,i這三天,現在要求計算d天后
Poj 1006 Biorhythms 中國剩餘定理
Description Some people believe that there are three cycles in a person's life that start the day he or she is born. These three cycles are the phys
【POJ 1006】【CRT(中國剩餘定理)模板題】Biorhythms
描述: Biorhythms Time Limit: 1000MS Memory Limit: 10000K Total Submissions: 130935 Accepted: 41750 Description Some people believe
poj 1006 Biorhythms(中國剩餘定理)
自己的題解略混亂(再看自己都沒看懂)所以還是貼一個神犇的講解(十分簡單易懂) 題目大意: 人有三個生理週期,給出三個週期的初始日期,請求出多少天后三個生理週期同時出現。 體力週期–23天 感情週
poj 1006 Biorhythms(中國剩餘定理的應用)
Biorhythms Time Limit: 1000MS Memory Limit: 10000K Total Submissions: 125633 Accepted: 39673 Description Some people believe that
POJ-1006-Biorhythms(中國剩餘定理)
Biorhythms Description Some people believe that there are three cycles in a person's life that start the day he or she is born. These
POJ 1006 ——Biorhythms 中國剩餘定理模板
Time Limit: 1000MS Memory Limit: 10000K Total Submissions: 112928 Accepted: 35337 Description Some people believe that there are th
【中國剩餘定理】POJ Biorhythms 1006
You will be given a number of cases. The input for each case consists of one line of four integers p, e, i, and d. The values p, e, and i are the number o
poj 1006 Biorhythms(中國剩餘定理)
題意: x === p ( mod 23 ) x === e ( mod 28 ) x === i ( mod 33 ) 給p e i ,求x 。 解析: 23 28 33互素,所以用中國剩餘定理做。 用之前的解同餘方程組的方法也試了試,很噁心,樣例裡面有0 0 0 0
poj 1006 生理週期 【中國剩餘定理】
生理週期 Time Limit: 1000MS Memory Limit: 10000K Total Submissions: 117999 Accepted: 37040 Description 人生來就有三個生理週期,分別為體力
中國剩餘定理 poj 1006 poj2891
Biorhythms Time Limit: 1000MS Memory Limit: 10000K Total Submissions: 129686 Accepted: 41277 Description Some people believe that
POJ 1006 Biorhythms (中國剩餘定理)
大意:有中文翻譯 思路:中國剩餘定理的完美詮釋 中國剩餘定理介紹 在《孫子算經》中有這樣一個問題:“今有物不知其數,三三數之剩二(除以3餘2),五五數之剩三(除以5餘3),七七數之剩二(除以7餘2),問物幾何?”這個問題稱為“孫子問題”,該問題的一般解法國際上稱
POJ 1006:Biorhythms 中國剩餘定理
Biorhythms Time Limit: 1000MS Memory Limit: 10000K Total Submissions: 121194 Accepted: 38157 Description Some people believe that
poj 2891 Strange Way to Express Integers 中國剩餘定理模板
Description Elina is reading a book written by Rujia Liu, which introduces a strange way to express non-negative integers. The way is descr
poj 2891 Strange Way to Express Integers 中國剩餘定理模板
Description Elina is reading a book written by Rujia Liu, which introduces a strange way to express non-negative integers. The way is d
Biorhythms POJ - 1006 中國剩余定理
occurs 中國剩余定理 天數 rip void 第一天 就是 spa csdn 定理證明:https://blog.csdn.net/d_x_d/article/details/48466957 https://blog.csdn.net/lyy289065406/ar
Hdu 1573 X問題 中國剩餘定理模板
Problem Description 求在小於等於N的正整數中有多少個X滿足:X mod a[0] = b[0], X mod a[1] = b[1], X mod a[2] = b[2], …, X mod a[i] = b[i], … (0 < a[i] <=