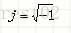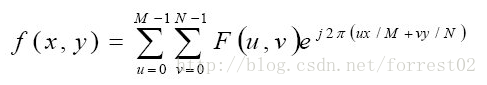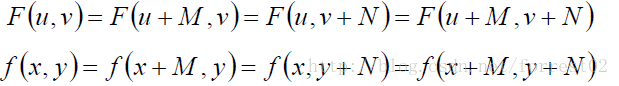數字影象處理-頻率域濾波原理
寫在前面的話
作者是一名在讀的碩士研究僧,方向是影象處理。由於影象處理是一門相對複雜的學科,作者在課堂上學到的東西只是非常淺顯的內容,我們老師說是,領我們進了個門。現在打算利用圖書館和網路上的資源進行自學。由於是剛開始寫自己的部落格,並且所具備的專業知識非常的有限,難免有出錯之處,如果有朋友發現一些毛病,希望能夠指正。哈哈,話不多說,進入正題。
作者使用的是岡薩雷斯的《數字影象處理(Matlab版)》,打算先用matlab先跟著書上的內容把程式碼先練一練。以後,再重新學習深入一些的知識。這裡不會將書中的全部內容都列一遍,我會選擇性的把重要的部分代實現。
頻率域
在介紹頻率域影象處理之前,先提幾個問題。
1.什麼是頻率域?
2.為什麼要在頻率域中進行影象處理?
頻率域的概念
頻率域是指從函式的頻率角度出發分析函式,和頻率域相對的是時間域。簡單說就是如果從時間域分析訊號時,時間是橫座標,振幅是縱座標。而在頻率域分析的時候則是頻率是橫座標,振幅是縱座標。
舉個例子,我們認為音樂是一個隨著時間變化的震動。但是如果站在頻域的角度上來講,音樂是一個隨著頻率變化的震動,這樣我們站在時間域的角度去觀察你會發現音樂是靜止的。同理,如果我們站在時間域的角度觀察頻率域的世界,就會發現世界是靜止的,也是永恆的。這是因為在頻率域是沒有時間的概念的,那麼也就沒有了隨著時間變化著的世界了。
另外,我們需要藉助傅立葉變換,才能夠在得到函式在頻率域中的資訊。
為什麼要在頻率域中進行影象處理?
1). 可以利用頻率成分和影象外表之間的對應關係。一些在空間域表述困難的增強任務,在頻率域中變得非常普通;
2). 濾波在頻率域更為直觀,它可以解釋空間域濾波的某些性質;
3).可以在頻率域指定濾波器,做反變換,然後在空間域使用結果濾波器作為空間域濾波器的指導
傅立葉變換
談到頻率域,就不得不說傅立葉變換了。傅立葉是18世紀法國的一位偉大的數學家。他最大的貢獻在於指出任何周期函式都可以表示為不同頻率的正弦和或者餘弦和的形式,每個正弦或者餘弦乘以不同的係數(也就是被大家所熟知的傅立葉級數)。無論函式有多複雜,只要它是週期性的,並且滿足一定的數學條件,就一定可以用這樣的正弦和或者餘弦和的形式來表示。甚至在有些情況下,非周期函式也可以用正弦和或者餘弦和的形式來表示。用傅立葉級數或變換表示的函式特徵可以完全通過傅立葉反變換來重建,而不會丟失任何資訊。而正是所謂的“傅立葉變換”使得我們可以工作於頻率域。
一維連續函式的fourier變換
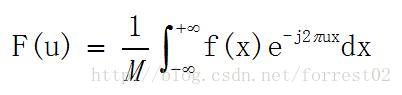
其中,f(x)表示原函式,F(u)表示變換之後的函式。u為頻率域變數。
一維連續函式的fourier反變換
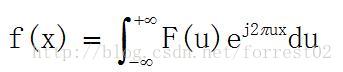
。。。公式編輯有點小麻煩,暫時先用截圖吧。請允許我小小的偷懶。。。
注意前面講過任何周期函式都可以被寫成若干個正弦波(餘弦波)的疊加。為了便於理解,在網上找了幾張圖片。
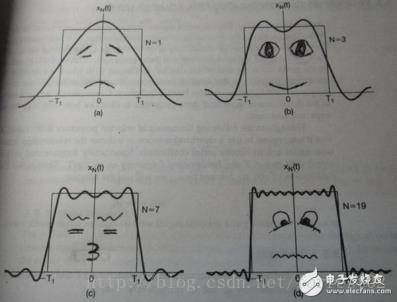
第一幅圖是一個鬱悶的餘弦波cos(x)
第二幅圖是2個賣萌的餘弦波的疊加cos(x)+a.cos(3x)
第三幅圖是4個“可愛”的餘弦波的疊加
第四幅圖是10個“難受”的餘弦波的疊加
隨著餘弦波數量逐漸的增長,最終疊加成一個標準的矩形,大家從中體會到了什麼?
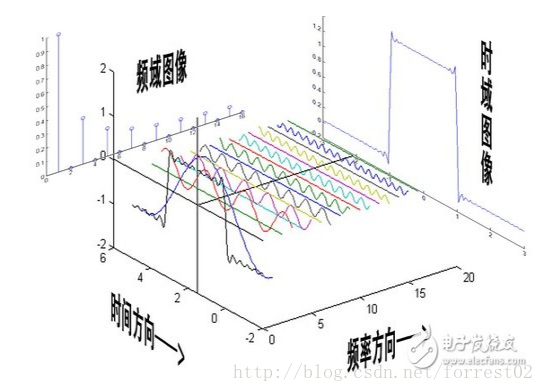
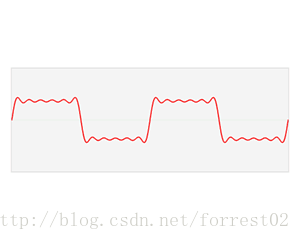
f為原影象, 傅立葉變換函式。傅立葉變換將函式的時域(紅色)與頻域(藍色)相關聯。頻譜中的不同成分。頻率在頻域中以峰值形式表示。
//這裡原圖是一幅動態圖,想看效果的朋友,請自行google傅立葉變換,weki上有動態圖。
二維離散傅立葉變換
影象尺寸為M*N的函式f(x,y)DFT為
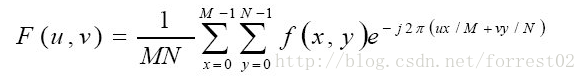
其中,u=0,1,2,…,M-1;v=0,1,2,…,N-1
給出F(u,v)由反DFT反變換可得到f(x,y)
傅立葉變換的基本概念:
1.頻譜
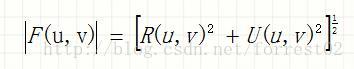
2.相位角
傅立葉變換的性質:
共軛對稱性
如果f(x,y)是實函式,則它的傅立葉變換具有 共軛對稱性
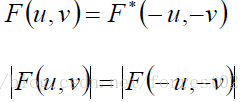
2 . 週期性
複習:當兩個複數實部相等,虛部互為相反數時,這兩個複數叫做互為共軛複數.
週期性和共軛對稱性
對於一維變換F(u),週期性是指F(u)的週期長度為M,對稱性是指頻譜關於原點對稱
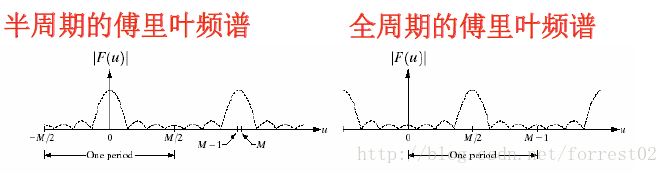
通過將原點的變換值移動到頻率矩形的中心位置,可簡化頻譜的
視覺分析。這可以通過在計算一維傅立葉變換之前將f(x)乘以 (-1)^x 來完成。
週期性和共軛對稱性舉例

通過將原點的變換值移動到頻率矩形的中心位置,可簡化頻譜的視覺分析。這可以通過在計算二維傅立葉變換之前將f(x,y)乘以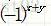
3. 平均值
由二維傅立葉變換的定義
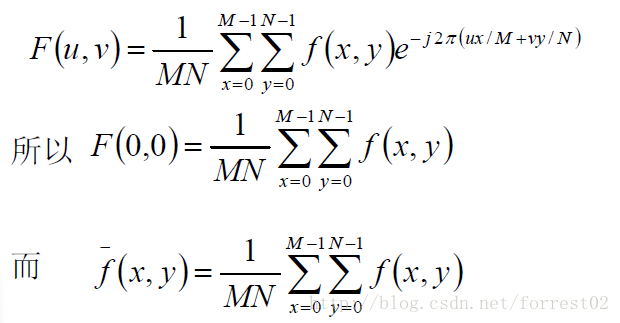
所以在原點的傅立葉變換等於影象f(x,y)的平均灰度級
4. 卷積定理
空間域和頻率域的基礎都是卷積定理
大小為M×N的兩個函式f(x,y)和h(x,y)的離散卷積
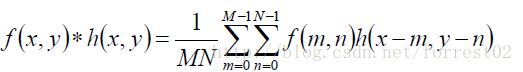
卷積定理
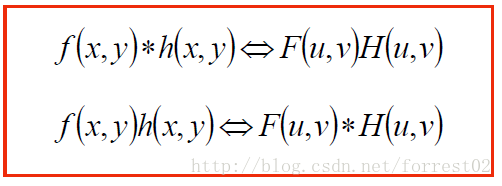
說明 第一個表示式表明:
兩個空間函式的卷積可以通過計算兩個傅立葉變換函式的乘積的逆變換得到。
相反,兩個空間函式卷積的傅立葉變換恰好等於兩個函式的傅立葉變換的乘積
頻率域濾波
低通濾波器:使低頻通過而使高頻衰減的濾波器
1.被低通濾波的影象比原始影象少尖銳的細節部分而突出平滑過渡部分
2.對比空間域濾波的平滑處理,如均值濾波器
高通濾波器:使高頻通過而使低頻衰減的濾波器
1.被高通濾波的影象比原始影象少灰度級的平滑過渡而突出邊緣等細節部分
2.對比空間域的梯度運算元、拉普拉斯運算元
低通濾波器

原影象的頻譜

低通濾波器示意圖

濾波效果
說明:這裡的低通濾波,意思就是把頻率低的波留下,把頻率高的波過濾掉。示意圖是經過居中處理的頻譜,就是從頻譜的中心到四周頻率由低到高。示意圖表示的是,留下中間低頻的,過濾點中心周圍高頻的部分。我們知道,低頻對應的影象中變化不明顯的部分,於是,影象就變的非常模糊。這在影象處理中也叫平滑濾波。再介紹一個概念:影象的銳化。就是與平滑化相對,即下面高通濾波器所達到的效果。很明顯,影象邊緣增強了。
高通濾波
原圖

原圖的頻譜

高通濾波器示意圖

效果圖

宣告:作者借鑑了一些前輩寫的內容,但因為這是之前在一個ppt中做彙報時使用的。時間已經過去了許久,已經很難在找到出處的連結了。但為了分享一些寫的很好的內容,就依舊貼出來了,在這裡表示感謝。
另外,由於是剛開始發表技術部落格所以,對於編輯的技巧還沒有熟練掌握,如果你看的不爽,那你就自己寫更漂亮的。哈哈
相關推薦
數字影象處理-頻率域濾波原理
寫在前面的話 作者是一名在讀的碩士研究僧,方向是影象處理。由於影象處理是一門相對複雜的學科,作者在課堂上學到的東西只是非常淺顯的內容,我們老師說是,領我們進了個門。現在打算利用圖書館和網路上的資源進行自學。由於是剛開始寫自己的部落格,並且所具備的專業知識非常的
[數字影象處理]頻域濾波(2)--高通濾波器,帶阻濾波器與陷波濾波器
close all; clear all; clc; %% ---------------------Add Noise------------------------- f = imread('left.tif'); f = mat2gray(f,[0 255]); [M,N] = size(f); P
數字影象處理——中值濾波
原理:模板中心對準待處理畫素,對模板下的對應畫素進行灰度值排序,將中值賦給當前畫素 Matlab程式碼: clear,clc; car = imread('sport car.pgm'); noise_car = imnoise(car,'salt & pepper',0.02);
【數字影象處理】線性濾波、最大值濾波,最小值濾波、中值濾波、高頻補償濾波(vs2017+openCV)
一、實驗原理 1、線性濾波 ① 不管是低通線性濾波還是高通線性濾波原理都是一樣的,用圖一所示的濾波器模板進行加權處理,將最終得到的R值賦給w5對應的畫素。 ②低通線性濾波和高通線性濾波不同之處就在於: 低通線性濾波w1+w2+…+w9 = 1,且w1~w9全
數字影象處理 維納濾波
function [f,noise] = mywiener2(g, nhood, noise) if (nargin<3) noise = []; end % Estimate the local mean of f. localMean = fil
數字影象處理,經典濾波演算法去噪對比實驗(Matlab實現)
一,經典濾波演算法的基本原理 1,中值濾波和均值濾波的基本原理 參考以前轉載的部落格:http://blog.csdn.net/ebowtang/article/details/38960271
(Opencv C++)數字影象處理-頻域增強
這裡我們將從兩個方面進行頻域增強的學習 一、任選兩幅影象(包括一副自備影象),計算其頻譜圖,並顯示 二、採用頻域濾波的方法進行影象降取樣和升取樣 一、首先計算其頻譜圖,用到的庫函式如下: CV_EXPO
數字影象處理-空間域影象增強(一)(影象反轉,對數變換,冪次變換、分段線性變換)
空間域增強的第一部分:影象反轉,對數變換,冪次變換、分段線性變換 (s:現點值,r: 原點值) 影象反轉: 這個無需多說,就是把黑變白,白變黑,拿八位灰度影象來說 表示式:s=255-r
數字影象處理中的頻率域濾波
作者是一名在讀的碩士研究僧,方向是機器視覺。由於視覺是一門相對複雜的學科,作者在課堂上學到的東西只是非常淺顯的內容,我們老師說是,領我們進了個門。現在打算利用圖書館和網路上的資源進行自學。由於是剛開始寫自己的部落格,並且所具備的專業知識非常的有限,難免有出錯之處,如果有朋友發現一些毛病,希望能夠指正
頻率域濾波基礎之二(讀數字影象處理學習halcon)
二維離散傅立葉(DFT)變化及其反傅立葉變換(IDFT) 傅立葉變換通用形式 對通用形式來講,c=1,s=-1即為傅立葉變化(影象空間域轉頻域);c=1/MN,s=1即為逆變換(頻域轉空間域) halcon運算元fft_generic(Image : ImageFFT
頻率域濾波基礎之五(讀數字影象處理學習halcon)
選擇性濾波 在很多應用中,其中感興趣是處理指定的頻段或頻率矩形。第一類濾波器分別稱為帶阻濾波器或帶通濾波器。第二類濾波器稱為陷波濾波器。 1、帶阻濾波和帶通濾波 D(u,v)是距離頻率矩形中心的距離,D0是頻寬的徑向中心,W是頻寬。一個帶同濾波器可以用從低通濾波器得到高通
python數字圖像處理(四) 頻率域濾波
urn nim turn 更多 都是 import ims sso frequency import matplotlib.pyplot as plt import numpy as np import cv2 %matplotlib inline 首先讀入這次需要使用的圖
數字影象處理之空間域濾波和銳化(Octave實現)
濾波這一概念可以結合數字訊號處理這一領域中的濾波。而在數字影象處理中濾波可以分為空間域濾波和頻率域濾波。這篇博文主要來學習下空間域濾波。 空間域濾波機理 *空間濾波器由一個鄰域(典型的是一個較小的矩形)構成,對該鄰域所包圍的畫素按照一定的操作計算出目標畫素的值,這一過程就是空
影象處理(3)頻率域濾波
Fourier變換 Fourier變換最開始由傅立葉提出,當時為了解決熱力學問題。後來經過發展形成了一套完整的理論,應用在物理學、訊號學等很多方面。如果一個函式滿足絕對可積條件,即: 因為計算機處理的是離散值,要求對f(x)和F(w)都取樣,這時Fourier變換被稱為離
數字影象處理筆記(八):頻域高通濾波銳化影象
1 - 引言 在筆記(七)中,我們通過衰減影象的傅立葉變換的高頻成分來平滑物件,因為邊緣和其他灰度的急劇變化與高頻分量有關,所以影象的銳化可在頻域通過高通濾波來實現。 一個高通濾波器是從給定的低通濾波器用下式得到:
數字影象處理筆記(七):頻域低通濾波平滑影象
1 - 傅立葉變換 在前面我們對空間濾波做了重點的研究,現在我們來介紹一下涉及頻率域中的各種濾波技術。影象從空間域轉換到頻率域使用的是二維傅立葉變換,一個畫素為M*N的影象f(x,y)進行傅立葉變換得到F(u,v),那麼一般的公式為:
數字影象處理筆記——頻域濾波、取樣和頻譜混疊( Frequency domain filtering; sampling and aliasing)
頻域濾波 頻域濾波就是將訊號先做傅立葉變換再與濾波器頻域響應相乘,最後再做傅立葉反變換得到 低通濾波器 讓我們先來看看理想低通濾波器,理想低通濾波器的頻率響應是一箇中間是1,周圍是0的正方形或圓形,而在時域上是sinc函式,,我們看經過低通濾波器後的影象變得模糊了,但是會發現圖中多
數字影象處理—彩色增強—偽彩色增強(亮度切割)(從灰度到彩色的變換)(頻域濾波)
一、偽彩色增強(從無彩色到有彩色): 一種常用的彩色增強方法是對原來灰度圖中不同灰度值的區域賦予不同的顏色以更明顯地區分它們。 二、主要有三種根據影象灰度的特點而賦予偽彩色的方法: 1、亮度切割:將影象灰度分級,然後對每個灰度值區間內的畫素賦一種顏色。 2、從灰度到彩色的變
系統學習數字影象處理之頻域濾波
最近在看模板匹配,雖然很簡單,但還是想認真過下基礎,因此把訊號處理頻域相關的內容,接著影象處理再過一遍。 理論上,對連續變數t的連續函式f(t)的傅立葉變換為F(u),利用f(t)取樣後的函式重建f(t),則必須滿足取樣定理,取樣函式的傅立葉變換為F'(U),它是連續週期的
使用 matlab 數字影象處理(九)—— 去卷積(deconvolution,逆濾波復原)
分享一下我老師大神的人工智慧教程!零基礎,通俗易懂!http://blog.csdn.net/jiangjunshow 也歡迎大家轉載本篇文章。分享知識,造福人民,實現我們中華民族偉大復興!