[數字影象處理]頻域濾波(2)--高通濾波器,帶阻濾波器與陷波濾波器
阿新 • • 發佈:2019-01-29
close all; clear all; clc; %% ---------------------Add Noise------------------------- f = imread('left.tif'); f = mat2gray(f,[0 255]); [M,N] = size(f); P = 2*M; Q = 2*N; fc = zeros(M,N); for x = 1:1:M for y = 1:1:N fc(x,y) = f(x,y) * (-1)^(x+y); end end F = fft2(fc,P,Q); H_NP = ones(P,Q); for x = (-P/2):1:(P/2)-1 for y = (-Q/2):1:(Q/2)-1 D = 2; v_k = -200; u_k = 150; D_k = ((x+u_k)^2 + (y+v_k)^2)^(0.5); H_NP(x+(P/2)+1,y+(Q/2)+1) = H_NP(x+(P/2)+1,y+(Q/2)+1) * 1/(1+(D/D_k)^4); D_k = ((x-u_k)^2 + (y-v_k)^2)^(0.5); H_NP(x+(P/2)+1,y+(Q/2)+1) = H_NP(x+(P/2)+1,y+(Q/2)+1) * 1/(1+(D/D_k)^4); v_k = 200; u_k = 150; D_k = ((x+u_k)^2 + (y+v_k)^2)^(0.5); H_NP(x+(P/2)+1,y+(Q/2)+1) = H_NP(x+(P/2)+1,y+(Q/2)+1) * 1/(1+(D/D_k)^4); D_k = ((x-u_k)^2 + (y-v_k)^2)^(0.5); H_NP(x+(P/2)+1,y+(Q/2)+1) = H_NP(x+(P/2)+1,y+(Q/2)+1) * 1/(1+(D/D_k)^4); v_k = 0; u_k = 250; D_k = ((x+u_k)^2 + (y+v_k)^2)^(0.5); H_NP(x+(P/2)+1,y+(Q/2)+1) = H_NP(x+(P/2)+1,y+(Q/2)+1) * 1/(1+(D/D_k)^4); D_k = ((x-u_k)^2 + (y-v_k)^2)^(0.5); H_NP(x+(P/2)+1,y+(Q/2)+1) = H_NP(x+(P/2)+1,y+(Q/2)+1) * 1/(1+(D/D_k)^4); v_k = 250; u_k = 0; D_k = ((x+u_k)^2 + (y+v_k)^2)^(0.5); H_NP(x+(P/2)+1,y+(Q/2)+1) = H_NP(x+(P/2)+1,y+(Q/2)+1) * 1/(1+(D/D_k)^4); D_k = ((x-u_k)^2 + (y-v_k)^2)^(0.5); H_NP(x+(P/2)+1,y+(Q/2)+1) = H_NP(x+(P/2)+1,y+(Q/2)+1) * 1/(1+(D/D_k)^4); H_NP(x+(P/2)+1,y+(Q/2)+1) = 1 + 700*(1 - H_NP(x+(P/2)+1,y+(Q/2)+1)); end end G_Noise = F .* H_NP; g_noise = real(ifft2(G_Noise)); g_noise = g_noise(1:1:M,1:1:N); for x = 1:1:M for y = 1:1:N g_noise(x,y) = g_noise(x,y) * (-1)^(x+y); end end %% ---------Bondpass Filters (Fre. Domain)------------ H_1 = ones(P,Q); for x = (-P/2):1:(P/2)-1 for y = (-Q/2):1:(Q/2)-1 D = (x^2 + y^2)^(0.5); D_0 = 250; W = 30; H_1(x+(P/2)+1,y+(Q/2)+1) = 1/(1+((D*W)/((D*D) - (D_0*D_0)))^6); end end G_1 = H_1 .* G_Noise; g_1 = real(ifft2(G_1)); g_1 = g_1(1:1:M,1:1:N); for x = 1:1:M for y = 1:1:N g_1(x,y) = g_1(x,y) * (-1)^(x+y); end end %% -----show------- close all; figure(); subplot(1,2,1); imshow(f,[0 1]); xlabel('a).Original Image'); subplot(1,2,2); imshow(log(1 + abs(F)),[ ]); xlabel('b).Fourier spectrum of a'); figure(); subplot(1,2,2); imshow(log(1 + abs(G_Noise)),[ ]); xlabel('c).Fourier spectrum of b'); subplot(1,2,1); imshow(g_noise,[0 1]); xlabel('b).Result of add noise'); figure(); subplot(1,2,1); imshow(H_1,[0 1]); xlabel('d).Butterworth Bandpass filter(D=355 W=40 n =2)'); subplot(1,2,2); h = mesh(1:20:Q,1:20:P,H_1(1:20:P,1:20:Q)); set(h,'EdgeColor','k'); axis([0 Q 0 P 0 1]); xlabel('u');ylabel('v'); zlabel('|H(u,v)|'); figure(); subplot(1,2,2); imshow(log(1 + abs(G_1)),[ ]); xlabel('e).Fourier spectrum of f'); subplot(1,2,1); imshow(g_1,[0 1]); xlabel('f).Result of denoise');
3.陷波濾波器(Notch Filter)
陷波濾波器也用於去除週期噪聲,雖然帶阻濾波器也能可以去除週期噪聲,但是帶阻濾波器對噪聲以外的成分也有衰減。而陷波濾波器主要對,某個點進行衰減,對其餘的成分不損失。使用下圖將更容易理解。
從空間域內看,影象存在著週期性噪聲。其傅立葉頻譜中,也能看到噪聲的所在之處(這裡我用紅圈標註出來了,他們不是資料的一部分)。我們如果使用帶阻濾波器的話,是非常麻煩的,也會使得影象有損失。陷波濾波器,能夠直接對噪聲處進行衰減,可以有很好的去噪效果。 其表示式如下所示,陷波濾波器可以通過對高通濾波器的中心,進行位移就可以得到了。
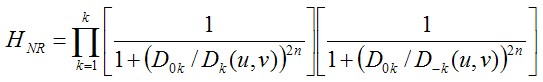
這裡,由於傅立葉的週期性,傅立葉頻譜上不可能單獨存在一個點的噪聲,必定是關於遠點對稱的一個噪聲對。這裡的
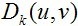
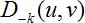 需要去除的噪聲點,其求取的方式如下所示。
需要去除的噪聲點,其求取的方式如下所示。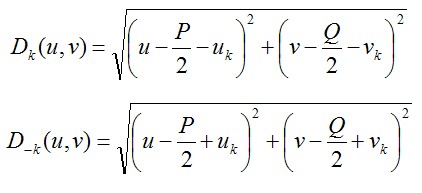 針對於上圖,我們設計如下濾波器,去進行去噪。
針對於上圖,我們設計如下濾波器,去進行去噪。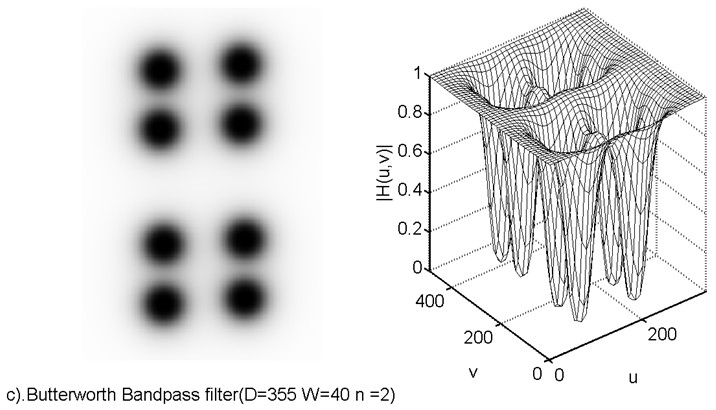 (圖片下標錯了,後續更新改過來!) 所得到的結果,如下所示。噪聲已經被去除了,畫質得到了很大的改善。
(圖片下標錯了,後續更新改過來!) 所得到的結果,如下所示。噪聲已經被去除了,畫質得到了很大的改善。
close all; clear all; clc; %% ---------Butterworth Notch filter (Fre. Domain)------------ f = imread('car_75DPI_Moire.tif'); f = mat2gray(f,[0 255]); [M,N] = size(f); P = 2*M; Q = 2*N; fc = zeros(M,N); for x = 1:1:M for y = 1:1:N fc(x,y) = f(x,y) * (-1)^(x+y); end end F = fft2(fc,P,Q); H_NF = ones(P,Q); for x = (-P/2):1:(P/2)-1 for y = (-Q/2):1:(Q/2)-1 D = 30; v_k = 59; u_k = 77; D_k = ((x+u_k)^2 + (y+v_k)^2)^(0.5); H_NF(x+(P/2)+1,y+(Q/2)+1) = H_NF(x+(P/2)+1,y+(Q/2)+1) * 1/(1+(D/D_k)^4); D_k = ((x-u_k)^2 + (y-v_k)^2)^(0.5); H_NF(x+(P/2)+1,y+(Q/2)+1) = H_NF(x+(P/2)+1,y+(Q/2)+1) * 1/(1+(D/D_k)^4); v_k = 59; u_k = 159; D_k = ((x+u_k)^2 + (y+v_k)^2)^(0.5); H_NF(x+(P/2)+1,y+(Q/2)+1) = H_NF(x+(P/2)+1,y+(Q/2)+1) * 1/(1+(D/D_k)^4); D_k = ((x-u_k)^2 + (y-v_k)^2)^(0.5); H_NF(x+(P/2)+1,y+(Q/2)+1) = H_NF(x+(P/2)+1,y+(Q/2)+1) * 1/(1+(D/D_k)^4); v_k = -54; u_k = 84; D_k = ((x+u_k)^2 + (y+v_k)^2)^(0.5); H_NF(x+(P/2)+1,y+(Q/2)+1) = H_NF(x+(P/2)+1,y+(Q/2)+1) * 1/(1+(D/D_k)^4); D_k = ((x-u_k)^2 + (y-v_k)^2)^(0.5); H_NF(x+(P/2)+1,y+(Q/2)+1) = H_NF(x+(P/2)+1,y+(Q/2)+1) * 1/(1+(D/D_k)^4); v_k = -54; u_k = 167; D_k = ((x+u_k)^2 + (y+v_k)^2)^(0.5); H_NF(x+(P/2)+1,y+(Q/2)+1) = H_NF(x+(P/2)+1,y+(Q/2)+1) * 1/(1+(D/D_k)^4); D_k = ((x-u_k)^2 + (y-v_k)^2)^(0.5); H_NF(x+(P/2)+1,y+(Q/2)+1) = H_NF(x+(P/2)+1,y+(Q/2)+1) * 1/(1+(D/D_k)^4); end end G_1 = H_NF .* F; g_1 = real(ifft2(G_1)); g_1 = g_1(1:1:M,1:1:N); for x = 1:1:M for y = 1:1:N g_1(x,y) = g_1(x,y) * (-1)^(x+y); end end %% -----show------- close all; figure(); subplot(1,2,1); imshow(f,[0 1]); xlabel('a).Original Image'); subplot(1,2,2); imshow(log(1 + abs(F)),[ ]); xlabel('b).Fourier spectrum of a'); figure(); subplot(1,2,1); imshow(H_NF,[0 1]); xlabel('c).Butterworth Notch filter(D=30 n=2)'); subplot(1,2,2); h = mesh(1:10:Q,1:10:P,H_NF(1:10:P,1:10:Q)); set(h,'EdgeColor','k'); axis([0 Q 0 P 0 1]); xlabel('u');ylabel('v'); zlabel('|H(u,v)|'); figure(); subplot(1,2,2); imshow(log(1 + abs(G_1)),[ ]); xlabel('e).Fourier spectrum of d'); subplot(1,2,1); imshow(g_1,[0 1]); xlabel('d).Result image');
原文發於部落格:http://blog.csdn.net/thnh169/
