通常，我們會遇到很多問題無法用分析的方法來求得精確解，例如由於式子特別，真的解不出來；

一般遇到這種情況，人們經常會採用一些方法去得到近似解（越逼近精確解越好，當然如果一個近似演算法與精確解的接近程度能夠通過一個式子來衡量或者有上下界，那麼這種近似演算法比較好，因為人們可以知道接近程度，換個說法，一般一個近似演算法被提出後，人們通常都會去考察或尋求刻劃近似程度的式子）。

本文要談的隨機模擬就是一類近似求解的方法，這種方法非常的牛逼哦，它的誕生雖然最早可以追溯到18xx年法國數學家蒲鬆的投針問題（用模擬的方法來求解\pi的問題），但是真正的大規模應用還是被用來解決二戰時候美國佬生產原子彈所碰到的各種難以解決的問題而提出的蒙特卡洛方法（Monte Carlo)，從此一發不可收拾。

本文將分為兩個大類來分別敘述，首先我們先談談隨機模擬的基本思想和基本思路，然後我們考察隨機模擬的核心：對一個分佈進行抽樣。我們將介紹常用的抽樣方法，1. 接受-拒絕抽樣；2）重要性抽樣；3）MCMC（馬爾科夫鏈蒙特卡洛方法）方法，主要介紹MCMC的兩個非常著名的取樣演算法（metropolis-hasting演算法和它的特例Gibbs取樣演算法）。

一. 隨機模擬的基本思想

我們先看一個例子：現在假設我們有一個矩形的區域R（大小已知），在這個區域中有一個不規則的區域M（即不能通過公式直接計算出來），現在要求取M的面積？ 怎麼求？近似的方法很多，例如：把這個不規則的區域M劃分為很多很多個小的規則區域，用這些規則區域的面積求和來近似M，另外一個近似的方法就是取樣的方法，我們抓一把黃豆，把它們均勻地鋪在矩形區域，如果我們知道黃豆的總個數S，那麼只要我們數數位於不規則區域M中的黃豆個數S1，那麼我們就可以求出M的面積：M=S1*R/S。

另外一個例子，在機器學習或統計計算領域，我們常常遇到這樣一類問題：即如何求取一個定積分：\inf _a ^b f(x) dx， 如歸一化因子等。

如何來求解這類問題呢？當然如果定積分可以解析求出，直接求出即可，如果不能解析求出，只能求取近似解了，常用的近似方法是採用蒙特卡洛積分，即把上述式子改寫為：

\inf _a^b f(x)*g(x)/g(x) dx = \inf _a^b (1/g(x)) *f(x)*g(x) dx

那麼把f(x)/g(x)作為一個函式，而把g(x)看做是[a,b]上的一個概率分佈，抽取n個樣本之後，上述式子可以繼續寫為：{\sum _1^n [f(x_i)/g(x_i)]}/n，當n趨向無窮大的時候，根據大數定理，上述式子是和要求的定積分式子是相等的，因此可以用抽樣的方法來得到近似解。

通過上述兩個例子，我們大概能夠理解抽樣方法解決問題的基本思想，其基本思路就是要把待解決的問題轉化為一種可以通過某種取樣方法可以解決的問題，至於怎麼轉化，還是挺有創造性，沒有定法。因此隨機模擬方法的核心就是如何對一個概率分佈得到樣本，即抽樣（sampling）。因此下一節，我們將介紹常用的抽樣方法。

（pku，sewm，shinning）

二. 常見的抽樣方法

2.0 直接抽樣法

略，因為較為簡單，而且只能解決很簡單的問題，一般是一維分佈的問題。

2.1 接受-拒絕抽樣（Acceptance-Rejection sampling)

又簡稱拒絕抽樣，直觀地理解，為了得到一個分佈的樣本，我們通過某種機制得到了很多的初步樣本，然後其中一部分初步樣本會被作為有效的樣本（即要抽取的分佈的樣本），一部分初步樣本會被認為是無效樣本捨棄掉。這個演算法的基本思想是：我們需要對一個分佈f(x)進行取樣，但是卻很難直接進行取樣，所以我們想通過另外一個容易取樣的分佈g(x)的樣本，用某種機制去除掉一些樣本，從而使得剩下的樣本就是來自與所求分佈f(x)的樣本。

它有幾個條件：1）對於任何一個x，有f(x)<=M*g(x); 2) g(x)容易取樣；3) g(x)最好在形狀上比較接近f(x)。具體的取樣過程如下：

1. 對於g(x)進行取樣得到一個樣本xi, xi ~ g(x);

2. 對於均勻分佈取樣 ui ~ U(a,b);

3. 如果ui<= f(x)/[M*g(x)], 那麼認為xi是有效的樣本；否則捨棄該樣本； （# 這個步驟充分體現了這個方法的名字：接受-拒絕）

4. 反覆重複步驟1~3，直到所需樣本達到要求為止。

這個方法可以如圖所示：

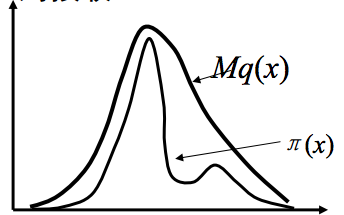
(說明：這是從其他地方弄來的圖，不是自己畫的，符號有些和文中不一致，其中\pi(x) 就是文中的f(x)，q(x)就是文中的g(x)  )

2.2 重要性抽樣(Importance sampling)

重要性取樣和蒙特卡洛積分密切相關，看積分：

\inf f(x) dx = \inf f(x)*(1/g(x))*g(x) dx, 如果g(x)是一個概率分佈，從g(x)中抽取N個樣本，上述的式子就約等於(1/N)* \sum f(xi)*(1/g(xi))。這相當於給每個樣本賦予了一個權重，g(xi)大意味著概率大，那麼N裡面含有這樣的樣本xi就多，即這些樣本的權重大，所以稱為重要性抽樣。

抽樣的步驟如下：

1. 選擇一個容易抽樣的分佈g(x), 從g(x)中抽取N個樣本；
2. 計算(1/N)* \sum f(xi)*(1/g(xi))，從而得到近似解。

（pku，sewm，shinning）

2.3  MCMC抽樣方法

無論是拒絕抽樣還是重要性取樣，都是屬於獨立取樣，即樣本與樣本之間是獨立無關的，這樣的取樣效率比較低，如拒絕取樣，所抽取的樣本中有很大部分是無效的，這樣效率就比較低，MCMC方法是關聯取樣，即下一個樣本與這個樣本有關係，從而使得采樣效率高。MCMC方法的基本思想是：通過構建一個markov chain使得該markov chain的穩定分佈是我們所要取樣的分佈f(x)。如果這個markov chain達到穩定狀態，那麼來自這個chain的每個樣本都是f(x)的樣本，從而實現抽樣的目的。這裡存在一個核心問題，如何構建滿足要求的markov chain？（什麼是markov chain，什麼是穩定分佈，請查資料，這裡假設讀者已知。）
在本文，我們介紹兩個著名MCMC抽樣方法，它們能夠方便地構建滿足要求的markov chain。

A).  Metropolis-Hasting演算法

這個演算法是兩個作者的合稱，但不是同一篇論文的，一個是1953年，另外一個是197x年對1953年的工作進行了一些擴充套件，所以以這兩位作者的名字來命名這個演算法。

假設要取樣的概率分佈是\pi(x)，現在假設有一個概率分佈p(y|x)，使得\pi(x)*p(y|x) = \pi(y)*p(x|y)成立，稱細緻平衡公式，這個細緻平衡公式是markov chain能達到穩定分佈的必要條件。因此關鍵是構建出一個概率分佈p(y|x)使得它滿足細緻平衡。現在假設我們有一個容易取樣的分佈q(y|x)（稱為建議分佈)，對於目前的樣本x，它能夠通過q(y|x)得到下一個建議樣本y，這個建議樣本y按照一定的概率被接受或者不被接受，稱為比率\alpha(x, y) = min{1, q(x|y)*\pi(y)/[q(y|x)*\pi(x)]}。即如果知道樣本xi，如何知道下一個樣本x_{i+1}是什麼呢？就是通過q(y|xi)得到一個建議樣本y，然後根據\alpha(xi, y)決定x_{i+1}=y 還是x_{i+1}=xi。可以證明分佈q(y|x)*\alpha(x,y)滿足細緻平衡，同時可以證明這樣抽取得到的樣本是分佈\pi(x)的樣本。具體的步驟如下：

1. 給定一個起始樣本x_0和一個建議分佈q(y|x)；

2. 對於第i個樣本xi，通過q(y|xi)得到一個建議樣本y；計算比率\alpha(xi, y)= min{1, q(xi|y)*\pi(y)/[q(y|xi)*\pi(xi)]};

3. 抽取一個均勻分佈樣本ui ~ U(0,1)，如果ui <= \alpha(xi,y)，則x_{i+1} = y；否則x_{i+1} = xi；

4. 重複步驟2~3，直到抽取到想要的樣本數量為止。

如果，建議分佈q(y|x) 滿足：q(y|x) = q(x|y)，即對稱，這個時候比率\alpha(x, y) = min{1, \pi(y)/\pi(x)}就是1953年最原始的演算法，後來hasting把這個演算法擴充套件了，不要求建議分散式對稱的，從而得到了上述的演算法。然而這個演算法有一個缺點，就是抽樣的效率不高，有些樣本會被捨棄掉。從而產生了Gibbs演算法。

B).  Gibbs取樣演算法

Gibbs演算法，很簡單，就是用條件分佈的抽樣來替代全概率分佈的抽樣。例如，X={x1,x2,...xn}滿足分佈p(X)，如何對p(X)進行抽樣呢？如果我們知道它的條件分佈p(x1|X_{-1}),...,p(xi|X_{-i}),....，其中X_{-i}表示除了xi之外X的所有變數。如果這些條件分佈都是很容易抽樣的，那麼我們就可以通過對條件分佈的抽樣來對全概率分佈p(X)進行抽樣。

Gibbs取樣演算法的步驟：

1. 給定一個初始樣本X0={x10,x20,...,xn0}

2.已知一個樣本Xi={x1i,x2i,...,xni}，對於x1_{i+1}進行抽樣，x1_{i+1} ~ p(x1|Xi_{-1})

3. 對於x2_{i+1}進行抽樣，x2_{i+1} ~ p(x2|x1_{i+1}, x3i,...xni)

................................................................

4.對於xn_{i+1}進行抽樣，xn_{i+1} ~ p(xn|x1_{i+1}, x2_{i+1},...x_{n-1}_{i+1})

5.步驟2~4可以得到X的一個樣本，然後重複步驟2~4可以不斷地得到X的樣本。

當然無論是metropolis-hasting演算法還是gibbs演算法，都有一個burn in的過程，所謂burn in的過程就是因為這個兩個演算法本身都是markov chain的演算法，要達到穩定狀態需要一定的步驟才能達到，所以需要一個burn in過程，只有在達到平衡狀態時候得到的樣本才能是平衡狀態時候的目標分佈的樣本，因此，在burn in過程中產生的樣本都需要被捨棄。如何判斷一個過程是否達到了平衡狀態還沒有一個成熟的方法來解決，目前常見的方法是看是否狀態已經平穩（例如畫一個圖，如果在較長的過程中，變化已經不大，說明很有可能已經平衡）當然這個方法並不能肯定一個狀態是否平衡，你可以舉出反例，但是卻是實際中沒有辦法的辦法。

可以證明Gibbs演算法是metropolis-hasting演算法的一個特例,即比率\alpha(x,y) = 1的一個特列。具體證明，此處略。

（pku，sewm，shinning）