斯特靈公式是一條用來取n階乘近似值的數學公式。一般來說，當n很大的時候，n階乘的計算量十分大，所以斯特靈公式十分好用。從圖中可以看出，即使在n很小的時候，斯特靈公式的取值已經十分準確。

公式為：   

從圖中看出，對於足夠大的整數n，這兩個數互為近似值。更加精確地：

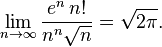            或者        

這個公式，以及誤差的估計，可以推導如下。我們不直接估計n!，而是考慮它的自然對數：

   

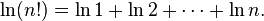
按一般方法計算N的階乘，其時間複雜度為O（N）：N！= 1 * 2 * 3 * 4 * 5 * ............ * N；

如果要計算N後得到的數字為幾位數，則我們可以知道其位數等於lgN！+1；

則: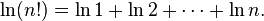 

但是當N很大的時候，我們可以通過斯特林公式進行優化：（即Stirling公式）

（e = 2.718）

斯特林公式可以用來估算某數的大小，結合lg可以估算某數的位數，或者可以估算某數的階乘是另一個數的倍數。

題目給出的N的範圍是: 1<= N <= 10⁷  

^{用普通方法肯定算不出N的階乘後的出的數字位數，但運用斯特林公式則很好解決.}

Stirling 公式

即：

    Stirling公式的意義在於：當n足夠大時，n!計算起來十分困難，雖然有很多關於n!的等式，但並不能很好地對階乘結果進行估計，尤其是n很大之後，誤差將會非常大。但利用Stirling公式可以將階乘轉化成冪函式，使得階乘的結果得以更好的估計。而且n越大，估計得越準確。

利用Stirling公式求解n!的位數：易知整數n的位數為[lgn]+1。利用Stirling公式計算n!結果的位數時，可以兩邊取對數，得:

故n!的位數為：