求二叉樹的最大葉子節點距離(遞迴)
題目: 輸入一顆二叉樹先序遍歷的字串,輸出該二叉樹的最大葉子節點距離
思路:先定義一個表示最大葉子節點距離的全域性變數,然後按照後續遍歷的方法訪問每一個節點,
在遍歷的過程中全域性變數隨時更新為目前出現的最大節點距離。當訪問完根節點後,全域性變數裡
的值即為最大葉節點距離。
節點型別定義如下:
struct BTNode
{
char key;
BTNode* lchild, *rchild;
int maxLeftDepth;
int maxRightDepth;
BTNode(char val) :key(val), lchild(NULL), rchild(NULL), maxLeftDepth(0), maxRightDepth(0) {};
}; //儲存最大葉子節點距離的全域性變數
int maxDepth = 0;
//按照先序遍歷的順序輸入一棵二叉樹的所有節點,#代表空節點,建立一顆二叉樹
void createTree(BTNode*& root) { char val = getchar(); if (val == '#') { root = NULL; return; } else { if (root == NULL) { root = new BTNode(val); createTree(root->lchild); createTree(root->rchild); } } }
//後序遍歷輸出二叉樹所有節點,驗證上面建立的二叉樹是否正確
void PostOrderTraversal(BTNode* root)
{
if (root == NULL)
return;
PostOrderTraversal(root->lchild);
PostOrderTraversal(root->rchild);
cout << root->key << " ";
}
//查詢最大葉子節點距離
//按後序遍歷的方式依次刪除二叉樹的每一個節點void maxLeafDistance(BTNode* root) { if (root == NULL) return ; //先訪問左孩子節點 if (root->lchild == NULL) root->maxLeftDepth = 0; if (root->lchild != NULL) maxLeafDistance(root->lchild); //再訪問右孩子節點 if (root->rchild == NULL) root->maxRightDepth = 0; if (root->rchild != NULL) maxLeafDistance(root->rchild); //最後訪問根節點 if (root->lchild) { int maxLeftDepOfRt = ((root->lchild->maxLeftDepth > root->lchild->maxRightDepth) ? root->lchild->maxLeftDepth + 1 : root->lchild->maxRightDepth + 1); root->maxLeftDepth = maxLeftDepOfRt; } if (root->rchild) { int maxRightDepOfRt = (root->rchild->maxLeftDepth > root->rchild->maxRightDepth) ? root->rchild->maxLeftDepth + 1 : root->rchild->maxRightDepth + 1; root->maxRightDepth = maxRightDepOfRt; } //訪問完根節點後依據需要更新代表最大葉子節點距離的全域性變數 if (root->maxLeftDepth + root->maxRightDepth >maxDepth) { maxDepth = root->maxLeftDepth + root->maxRightDepth; } return ; }
void destroyTree(BTNode*& root)
{
if (root != NULL)
{
if (root->lchild == NULL && root->rchild == NULL)
{
cout << "刪除" << root->key << "節點" << endl;
delete root;
root = NULL;
return;
}
destroyTree(root->lchild);
destroyTree(root->rchild);
cout << "刪除" << root->key << "節點" << endl;
delete root;
root = NULL;
}
else
return;
}//main函式
int main()
{
BTNode* root = NULL;
cout << "請按先序遍歷順序輸入一顆二叉樹,#代表空節點: ";
createTree(root);
cout << "建立的二叉樹的後序遍歷順序為: ";
PostOrderTraversal(root);
cout << endl;
maxLeafDistance(root);
cout << "構造的二叉樹中最大葉子節點距離為: " << maxDepth << endl;
destroyTree(root);
return 0;
}整理一下全部的程式碼:
#include<iostream>
using namespace std;
struct BTNode
{
char key;
BTNode* lchild, *rchild;
int maxLeftDepth;
int maxRightDepth;
BTNode(char val) :key(val), lchild(NULL), rchild(NULL), maxLeftDepth(0), maxRightDepth(0) {};
};
int maxDepth = 0;//代表最大葉子節點距離的全域性變數
void createTree(BTNode*& root)
{
char val = getchar();
if (val == '#')
{
root = NULL;
return;
}
else
{
if (root == NULL)
{
root = new BTNode(val);
createTree(root->lchild);
createTree(root->rchild);
}
}
}
void PostorderTraversal(BTNode* root)
{
if (root == NULL)
return;
PostorderTraversal(root->lchild);
PostorderTraversal(root->rchild);
cout << root->key << " ";
}
void maxLeafDistance(BTNode* root)
{
if (root == NULL)
return ;
//先訪問左孩子節點
if (root->lchild == NULL)
root->maxLeftDepth = 0;
if (root->lchild != NULL)
maxLeafDistance(root->lchild);
//再訪問右孩子節點
if (root->rchild == NULL)
root->maxRightDepth = 0;
if (root->rchild != NULL)
maxLeafDistance(root->rchild);
//最後訪問根節點
if (root->lchild)
{
int maxLeftDepOfRt = ((root->lchild->maxLeftDepth > root->lchild->maxRightDepth) ? root->lchild->maxLeftDepth + 1 :
root->lchild->maxRightDepth + 1);
root->maxLeftDepth = maxLeftDepOfRt;
}
if (root->rchild)
{
int maxRightDepOfRt = (root->rchild->maxLeftDepth > root->rchild->maxRightDepth) ? root->rchild->maxLeftDepth + 1 :
root->rchild->maxRightDepth + 1;
root->maxRightDepth = maxRightDepOfRt;
}
//訪問完根節點後依據需要更新代表最大葉子節點距離的全域性變數
if (root->maxLeftDepth + root->maxRightDepth >maxDepth)
{
maxDepth = root->maxLeftDepth + root->maxRightDepth;
}
return ;
}
void destroyTree(BTNode*& root)
{
if (root != NULL)
{
if (root->lchild == NULL && root->rchild == NULL)
{
cout << "刪除" << root->key << "節點" << endl;
delete root;
root = NULL;
return;
}
destroyTree(root->lchild);
destroyTree(root->rchild);
cout << "刪除" << root->key << "節點" << endl;
delete root;
root = NULL;
}
else
return;
}
int main()
{
BTNode* root = NULL;
cout << "請按先序遍歷順序輸入一顆二叉樹,#代表空節點: ";
createTree(root);
cout << "建立的二叉樹的後序遍歷順序為: ";
PostorderTraversal(root);
cout << endl;
maxLeafDistance(root);
cout << "構造的二叉樹中最大葉子節點距離為: " << maxDepth << endl;
destroyTree(root);
return 0;
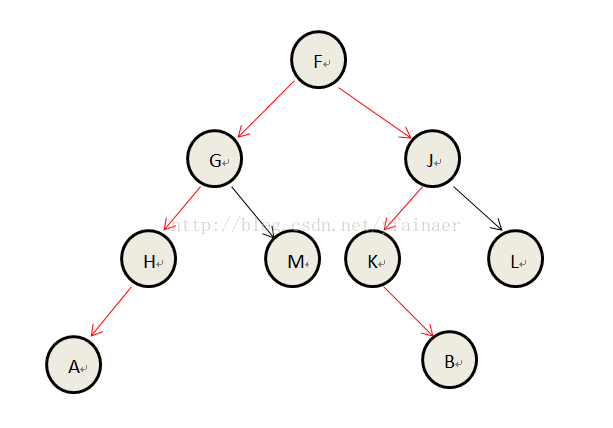
}測試用例1:FGHA###M##JK#B##L##
構建的二叉樹如下圖所示:
知紅色路徑上的兩個葉子節點為最大距離葉子節點,距離為6。
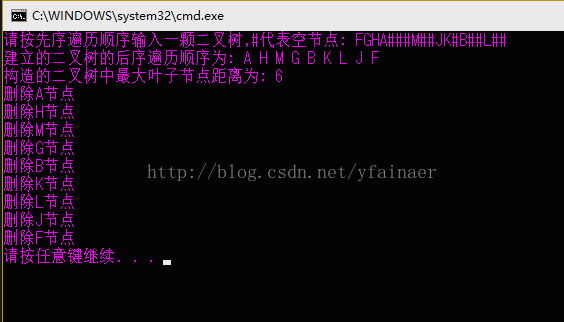
執行結果如下圖所示:
從上圖可以看到執行結果正確,說明程式編碼無誤。
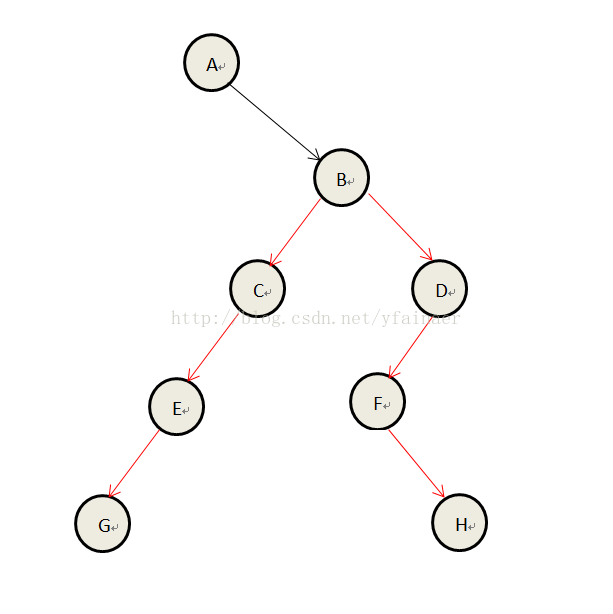
測試用例2:A#BCEG####DF#H###
構建的二叉樹如下圖所示:
知紅色路徑上的兩個葉子節點為最大距離葉子節點,距離為6。
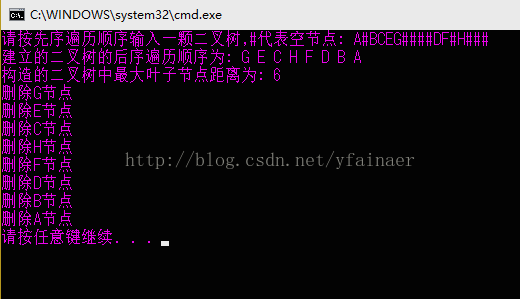
執行結果如下圖所示:
從上圖可以看到執行結果正確,說明程式編碼無誤。
相關推薦
求二叉樹最大葉子節點距離(不含全域性變數)
題目: 輸入一顆二叉樹先序遍歷的字串,輸出該二叉樹的最大葉子節點距離 分析知,最大的距離要麼是經過根節點的一條路徑,要麼是在左子樹中的一條路徑,或者是在右子樹中的一條路徑。 那麼可以知道最大葉子節點的距離是左右子樹的高度和、左子樹最大葉節點距離、右子樹最大葉節點距
求二叉樹的最大葉子節點距離(遞迴)
題目: 輸入一顆二叉樹先序遍歷的字串,輸出該二叉樹的最大葉子節點距離 思路:先定義一個表示最大葉子節點距離的全域性變數,然後按照後續遍歷的方法訪問每一個節點, 在遍歷的過程中全域性變數隨時更新為目前出現的最大節點距離。當訪問完根節點後,全域性變數裡 的值即為最大葉節點距
利用棧結構實現二叉樹的非遞迴遍歷,求二叉樹深度、葉子節點數、兩個結點的最近公共祖先及二叉樹結點的最大距離
原文地址:http://blog.csdn.net/forbes_zhong/article/details/51227747 利用棧實現二叉樹的非遞迴遍歷,並求二叉樹的深度、葉子節點數、兩個節點的最近公共祖先以及二叉樹結點的最大距離,部分參考《劍指offer》這本書
求二叉樹最大最小深度
als 最小 log root roo null mat dep tde 1.求二叉樹最大深度 public int maxDepth(TreeNode root) { if(root==null){ return 0;
求二叉樹的前中後序遞迴、迭代,樹的葉子節點,高度(c語言)
#include<stdio.h> #include<string.h> #include<stdlib.h> #include<assert.h> #define MAX 100 typedef struct n
查詢二叉樹最大值節點
如題 : 在二叉樹中查詢最大值的節點並返回 測試資料 : {1,-5,3,1,2,-4,-5} 答案 : 3 思路 : 從根節點往下分別查詢左子樹和右子樹的最大節點,再比較左子樹,右子樹,根節點的大小
ODOA(2) 求二叉樹中兩個節點的最大距離(C語言實現)
問題描述; 如果我們把二叉樹看成一個圖,父子節點之間的連線看成是雙向的,我們姑且定義"距離"為兩節點之間邊的個數。寫一個程式求一棵二叉樹中相距最遠的兩個節點之間的距離。 演算法很容易想得到: 如果根節點的左子樹或右子樹為空,那麼最大距離即為樹的深度否則,最大距離等於
阿里14筆試題-求一個二叉樹最大值和最小值的差值絕對值
阿里巴巴面試題: 輸入:一個二叉樹 輸出:二叉樹的最大值和最小值的差值絕對值 單純從演算法功能上來看 1-可以先建立一個大根堆,把最大的元素挑出來; 2-然後在建立小根堆,把最小的元素挑出來; 3-在求最大和最小差值的絕對值; 程式碼: #if 0 /* 最大堆排序 */
求二叉樹中兩個節點最遠的距離
一說到二叉樹,就有很多題目,今天在程式設計之美中看到了二叉樹中兩個節點最遠的距離。所以給想借機寫一篇部落格。 在開始之前,我們先想想,兩個最常節點的最遠距離是怎麼樣的? 情況一:最大距離可能一個在左子
求二叉樹中兩個節點的最小公共祖先(LCA)
題目要求:求二叉樹中兩個節點p,q的最低公共祖先節點 首先,題目中沒有明確說明節點的結構,所以思考了一會然後問面試官節點有沒有父指標,面試官說有沒有父指標有影響嗎?我說有,然後他笑著說你來說說看。當時,只做出來有父指標的情況,沒有父指標的情況壓根想不出來。後
CODEVS 1501二叉樹最大寬度和高度
它的 logs nbsp 二叉 ace 最小寬度 最大 -h blog 題目描述 Description 給出一個二叉樹,輸出它的最大寬度和高度。 輸入描述 Input Description 第一行一個整數n。 下面n行每行有兩個數,對於第i行的兩個數
18.2.14 codevs1501 二叉樹最大寬度和高度
isp 連接 左右 ron esp color 整數 end codevs 題目描述 Description 給出一個二叉樹,輸出它的最大寬度和高度。 輸入描述 Input Description 第一行一個整數n。 下面n行每行有兩
二叉樹最大深度和最小深度
str treenode oot null 避免 結果 一個 blog clas 最大深度: int maxDepth(TreeNode *root) { if(root == NULL) return 0;
2018.3.26 1501 二叉樹最大寬度和高度
一個空格 post 12px 一行 個數 padding pac ide urn 題目描述 給出一個二叉樹,輸出它的最大寬度和高度。 輸入描述 第一行一個整數n。下面n行每行有兩個數,對於第i行的兩個數,代表編號為i的節點所連接的兩個左右兒子的編號。如果沒有某個兒子
LeetCode之二叉樹最大深度(簡單 二叉樹)
問題描述: 給定一個二叉樹,找出其最大深度。 二叉樹的深度為根節點到最遠葉子節點的最長路徑上的節點數。 說明: 葉子節點是指沒有子節點的節點。 示例: 給定二叉樹 [3,9,20,null,null,15,7], 3 / \ 9 20
LeetCode662 二叉樹最大寬度
給定一個二叉樹,編寫一個函式來獲取這個樹的最大寬度。樹的寬度是所有層中的最大寬度。這個二叉樹與滿二叉樹(full binary tree)結構相同,但一些節點為空。 每一層的寬度被定義為兩個端點(該層最左和最右的非空節點,兩端點間的null節點也計入長度)之間的長度。 示例 1: 輸入:
二叉樹最大深度(遞迴實現python)---LeetCode
# Definition for a binary tree node. # class TreeNode: # def __init__(self, x): # self.val = x # self.left = None #
leetcode662. 二叉樹最大寬度
題目連結: https://leetcode-cn.com/problems/maximum-width-of-binary-tree/ 題目: 給定一個二叉樹,編寫一個函式來獲取這個樹的最大寬度。樹的寬度是所有層中的最大寬度。這個二叉樹與滿二叉樹(full binary tree)結構
leetcode 662二叉樹最大寬度
一開始的思路是用bfs,但是感覺處理起來比較麻煩,後續會更新bfs的方法,這裡先貼上dfs的方法。 /** * Definition for a binary tree node. * struct TreeNode { * int val; * T
7-4 輸出一棵給定二叉樹的所有葉子節點
//輸出一棵給定二叉樹的所有葉子節點 #include "btree.cpp" void DispLeaf(BTNode *b) { if (b!=NULL) { if (b->lchild==NULL && b->rchild==NUL