問題描述；

如果我們把二叉樹看成一個圖，父子節點之間的連線看成是雙向的，我們姑且定義"距離"為兩節點之間邊的個數。寫一個程式求一棵二叉樹中相距最遠的兩個節點之間的距離。

演算法很容易想得到：

• 如果根節點的左子樹或右子樹為空，那麼最大距離即為樹的深度
• 否則，最大距離等於左子樹的深度+右子樹的深度

雖然這個問題很簡單，但是在實現的時候，還樹出了點問題，導致卡了兩天才實現。 原因： 1 樹的基本操作的實現不熟練 2 對遞迴的使用不熟悉 3 在遞迴建樹的時候，輸入序列一直沒搞清楚。。 經驗： 1 遇到樹，首先想到的是遞迴處理 2 使用遞迴，一定要有一個終止條件 3 強型別語言真心不方便，比如節點值設定為整形，那麼讀入的一定要是整形（強制型別轉換除外），導致必須要用一個數字（我用的0）表示空節點（即遞迴的終止條件）。 4 鞏固了樹的基本演算法，是在這個問題上的最大的收穫，只有真正實現它了，才能從更深的層次掌握它。 程式碼如下： 依然只是很簡單的實現，並沒有過多的異常處理。

/* 
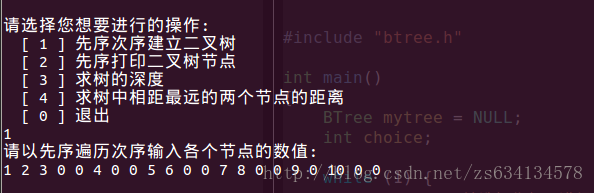
  Name: main.c 
  Author: suzhou 
  Date:   2014.02.18
  Num.    2
 */  


#include "btree.h"

int main()
{
	BTree mytree = NULL;
	int choice;
	
	while (1) {
		printf("\n請選擇您想要進行的操作:\n");
		printf("  [ 1 ] 先序次序建立二叉樹\n");
		printf("  [ 2 ] 先序列印二叉樹節點\n");
		printf("  [ 3 ] 求樹的深度\n");
		printf("  [ 4 ] 求樹中相距最遠的兩個節點的距離\n");
		printf("  [ 0 ] 退出\n");

		scanf("%d", &choice);

		switch(choice)
		{
		case 0:
			printf("%s\n", "謝謝使用");
			exit(0);
		case 1:
			printf("%s",
				   "請以先序遍歷次序輸入各個節點的數值:\n");
			createBTree(&mytree);
			continue;
		case 2:
			preOrderVisit(mytree);
			continue;
		case 3:
			printf("樹的深度為: %d\n",
				   depth(mytree));
			continue;
		case 4:
			printf("最大距離為： %d\n",
				   maxDistance(mytree)
				);
			continue;
		default:
			printf("%s\n",
				   "請輸入正確的選擇");
			continue;
		}
	}
	
	printf("Congratulations! It works!\n");
	return 0;
}
 

/* 
  Name: btree.h
  Author: suzhou 
  Date:   2014.02.18
  Num.    2
 */  




#ifndef BTREE
#define BTREE

#include "stdio.h"
#include "stdlib.h"

typedef struct BTNode
{
	int val;
	struct BTNode* pLeft;
	struct BTNode* pRight;
}BTNode, *BTree;


/*
  建立二叉樹
 */
void createBTree (
	BTree* tree
	);

/*
  先序遍歷二叉樹
 */
void preOrderVisit (
	BTree tree
	);

/*
  按樹狀列印節點
 */
void printTree (
	BTree tree,
	int depth
	);


/*
 * 求樹的深度
 */
int depth(
	BTree tree
	);

/*
 * 求樹的兩個節點的最遠距離
 */
int maxDistance(
	BTree tree
	);

#endif
 

/* 
  Name: btree.c 
  Author: suzhou 
  Date:   2014.02.18
  Num.    2
 */  



#include "btree.h"


/*
  建立二叉樹
 */
void createBTree (
	BTree* tree
	)
{
	int val;
	
	scanf("%d", &val);

	if ( val == 0 )
	{
		*tree = NULL;
	}
	else
	{
		*tree = (BTNode*) malloc (sizeof(BTNode));
		(*tree)->val = val;
		createBTree(&((*tree)->pLeft));
		createBTree(&((*tree)->pRight));
	}
}


/*
  先序遍歷二叉樹
 */
void preOrderVisit (
	BTree tree
	)
{
	if ( tree != NULL )
	{
		printf("%d\n", tree->val);
		preOrderVisit(tree->pLeft);
		preOrderVisit(tree->pRight);
	}
}


/*
  按樹狀列印節點
 */
void printTree (
	BTree tree,
	int depth
	)
{
	int i;
	
	if ( tree == NULL )
		return;
	for ( i=depth; i>=0; i-- )
		printf("%c", ' ');
	printf("%d\n" , tree->val);

	printTree(tree->pLeft, depth+1);
	printTree(tree->pRight, depth+1);
	
}


/*
 * 求樹的深度
 */
int depth(
	BTree tree
	)
{
	if (tree == NULL)
		return 0;
	else
		return 1 + 
			(depth(tree->pLeft) >= depth(tree->pRight)
			? depth(tree->pLeft) : depth(tree->pRight));
}


/*
 * 求樹的兩個節點的最遠距離
 */
int maxDistance(
	BTree tree
	)
{
	if (tree->pLeft == NULL
		|| tree->pRight == NULL)
		return depth(tree);
	else
		return depth(tree->pLeft) + depth(tree->pRight);
}

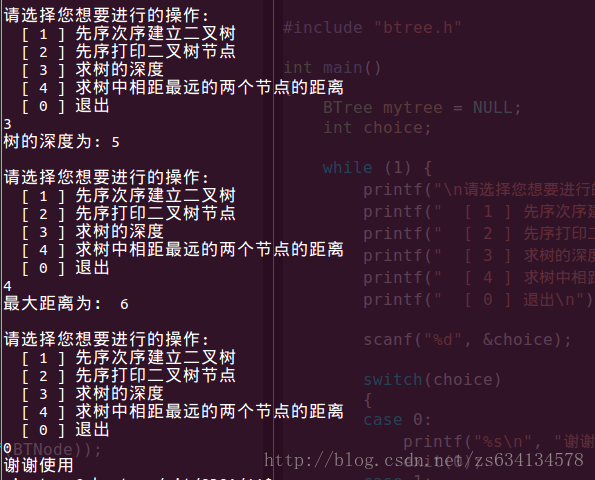
執行截圖：