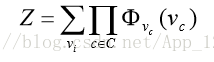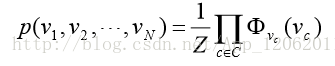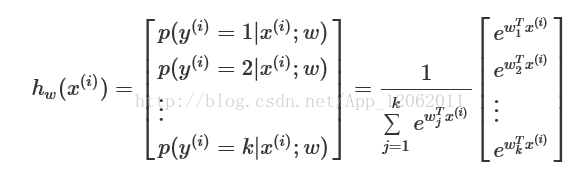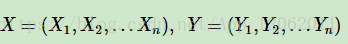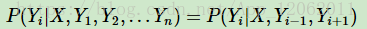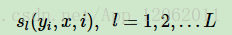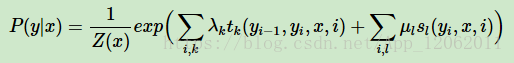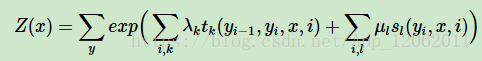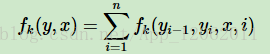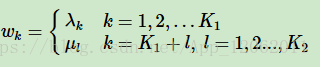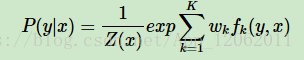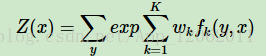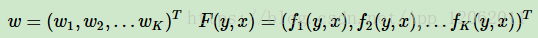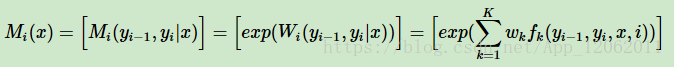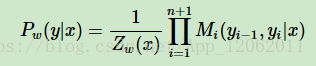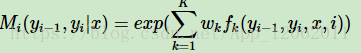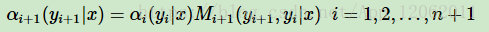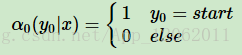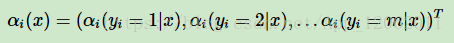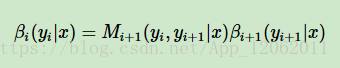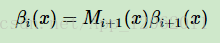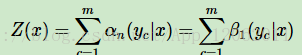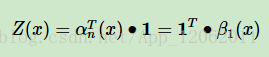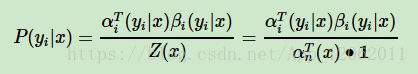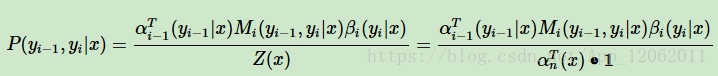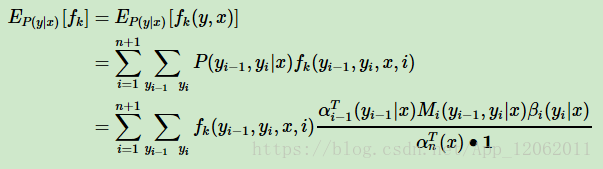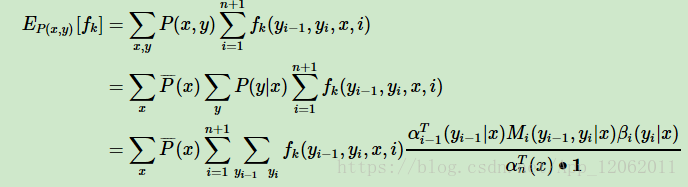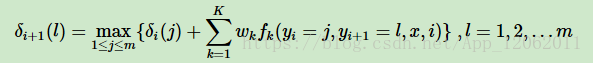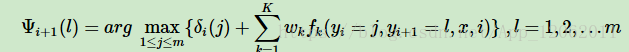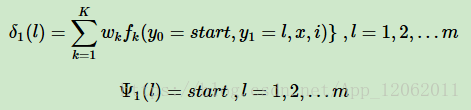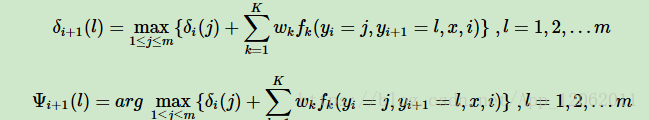條件隨機場(Conditional random fields)，是一種判別式圖模型，因為其強大的表達能力和出色的效能，得到了廣泛的應用。從最通用角度來看，CRF本質上是給定了觀察值集合 (observations)的馬爾可夫隨機場（MRF）。在這裡，我們直接從最通用的角度來認識和理解CRF，最後可以看到，線性CRF和所謂的高階CRF，都是某種特定結構的CRF。
1. 隨機場
簡單地講，隨機場可以看成是一組隨機變數的集合（這組隨機變數對應同一個樣本空間）。當然，這些隨機變數之間可能有依賴關係，一般來說，也只有當這些變數之間有依賴關係的時候，我們將其單獨拿出來看成一個隨機場才有實際意義。
2. Markov隨機場(MRF)

這是加了Markov性質限制的隨機場。首先，一個Markov隨機場對應一個無向圖。這個無向圖上的每一個節點對應一個隨機變數，節點之間的邊表示節點對應的隨機變數之間有概率依賴關係。因此，Markov隨機場的結構本質上反應了我們的先驗知識——哪些變數之間有依賴關係需要考慮，而哪些可以忽略。Markov性質是指，對Markov隨機場中的任何一個隨機變數，給定場中其他所有變數下該變數的分佈，等同於給定場中該變數的鄰居節點下該變數的分佈。這讓人立刻聯想到馬式鏈的定義：它們都體現了一個思想：離當前因素比較遙遠(這個遙遠要根據具體情況自己定義）的因素對當前因素的性質影響不大。
Markov性質可以看作是Markov隨機場的微觀屬性，那麼其巨集觀屬性就是其聯合概率的形式。
假設MRF的變數集合為
S=｛y1,…yn},
P(y1,…yn)= 1/Z * exp{-1/T * U(y1,..yn)},
其中Z是歸一化因子，即對分子的所有y1,..yn求和得到。U(y1,..yn)一般稱為能量函式（energy function）, 定義為在MRF上所有團的勢函式（clique-potential）之和。T稱為溫度，一般取1。什麼是團勢函式clique-potential呢? 就是在MRF對應的圖中，每一個團（clique）對應一個函式，稱為團勢函式（clique-potential）。（補充：團是馬爾科夫無向圖中，節點的集合使得該集合中任意兩個節點之間都存在一條邊，不採用條件概率，在無向圖中用勢函式來體現區域性約束，不必有概率解釋，且有更大的自由度，偏愛某種區域性配置，而不是其他區域性配置）。這個聯合概率形式又叫做吉布斯分佈（Gibbs distribution）。Hammersley and Clifford定理表達了這兩種屬性的等價性。
如果團勢函式的定義和團在圖中所處的位置無關，則稱該MRF是齊次的；如果團勢函式的定義和 團在圖中的朝向(orientation)無關，則稱該MRF是各向的。一般來說，為了簡化計算，都是假定MRF即是 齊次的，也是各向的。

補充：

儘管在給定每個節點的條件下，分配給該節點一個條件概率是可能的，但條件隨機場的無向性很難保證每個節點在給定它的鄰接點條件下得到的條件概率和以圖中其它節點為條件得到的條件概率一致。因此導致我們不能用條件概率引數化表示聯合概率，而要從一組條件獨立的原則中找出一系列區域性函式的乘積來表示聯合概率

。選擇區域性函式時，必須保證能夠通過分解聯合概率使沒有邊的兩個節點不出現在同一區域性函式中。簡單的區域性函式是定義在圖結構中的大團(clique)上的勢函式(Potential function)，並且是嚴格正實值的函式形式。但是一組正實數函式的乘積並不能滿足概率公理，則必須引入一個歸一化因子Z ，這樣可以確保勢函式的乘積滿足概率公理，且是G 中節點所表示的隨機變數的聯合概率分佈。

其中C 為大團集合，利用 Hammersley-Clifford 定理，可以得到聯合概率公式如下： 

基於條件獨立的概念，條件隨機場的無向圖結構可以用來把關於 Υv ∈Υ 的聯合分佈因式化正的和實值的勢函式的乘積，每個勢函式操作在一個由G中頂點組成的隨機變數子集上。根據無向圖模型條件獨立的定義，如果兩個頂點間沒有邊，則意味著這些頂點對應的隨機變數在給定圖中其它頂點條件下是條件獨立的。所以在因式化條件獨立的隨機變數聯合概率時，必須確保這些隨機變數不在同一個勢函式中。滿足這個要求的容易的方法是 要求每個勢函式操作在一個圖G 的大團上，這些大團由隨機變數相應頂點組成。這確保了沒有邊的頂點在不同的勢函式中，在同一個大團中的頂點都是有邊相連的。在無向圖 中，任何一個全連通（任意兩個頂點間都有邊相連）的子圖稱為一個團(clique)，而稱不能被其它團所包含的才為大團(maximal clique)。
3.從Markov隨機場到CRF
現在，如果給定的MRF中每個隨機變數下面還有觀察值，我們要確定的是給定觀察集合下，這個MRF的分佈，也就是條件分佈，那麼這個MRF就稱為 CRF(Conditional Random Field)。它的條件分佈形式完全類似於MRF的分佈形式,只不過多了一個觀察集合x，即P(y1,..yn|x) = 1/Z(x) * exp{ -1/T * U(y1,…yn,x)。U(y1,..yn,X)仍舊是click-potential之和。

來點正式的：

關聯資料有兩個特點：第一，我們準備建立模型的實體之間存在統計依賴性，第二，每個實體自身具有豐富的有利於分類的特徵例如，當Web文件進行分類時候，網頁上的文字類標籤提供了很多資訊，但超連結定義的頁面之間的關係，可以進一步提高分類的準確度，圖模型很自然的建立了實體之間的結構化關係。通常來講，圖模型已被用於表示聯合概率分佈P(Y,X)，其中的變數y代表我們希望預測的屬性，輸入變數X代表獲得的實體資訊。利用關係資料中的區域性特徵對聯合分佈建模非常困難，因為這需要對包含複雜依賴關係的P(X)建模，引入資料之間的關係是把雙刃劍，如果模型中引入它，導致模型非常複雜，如果忽略它，那麼模型的準確性就會受到影響.對於分類問題來說，直接模擬的條件分佈P(Y|X)條件隨機場就是這麼做的。條件隨機場是關聯這一個圖結構的條件分佈P(Y| X)，因為直接對條件概率建模，輸入變數X之間的關聯不需要顯示的表達出來

通常我看到一個模型，我總是會試著和我所知道的一些模型去進行比較。CRF算是機器學習模型中比較複雜的一個模型。同輸入輸出角度， CRF從資料空間來看是一個序列化的輸入和序列化的輸出， 從函式空間角度，就是一個指數函式，和邏輯迴歸函式形式一致，只是他的輸出是一個序列（一條句子）或者一個矩陣（一副影象），損失函式是cross entropy，優化演算法一般採用梯度下降類演算法（LBFGS)，但是在優化的過程中伴隨著複雜的inference過程。

判別式模型和產生式模型

樸素貝葉斯和邏輯迴歸模型之間的一個重要區別是，樸素貝葉斯是產生式模型，它基於聯合分佈P(X,Y)建模，而邏輯迴歸是判別式模型,它直接對條件分佈P(Y|X)建模，這一段中我們討論產生式模型和判別式模型的區別和判別式模型在很多應用中的優點，具體來說，我們會集中以樸素貝葉斯和邏輯迴歸為例，但是這些區別可以推廣到一般的產生式模型和判別式模型。
對條件分佈p（Y| X）建模，不包括對P(X) 建模（P(X)對分類來說無關緊要），對P(X)建模非常困難，因為P(X)包含很多相互依賴的特徵,比如在 NER應用中，HMM只依賴一個特徵，這個詞本身，但是很多詞，特別是一些特定的名字可能沒有出現在訓練集合中，因此詞本身這個特徵是未知的，為了標註未登陸詞，我們需要利用詞的其他的特徵，如詞性，相鄰詞，字首和字尾等。
在產生式模型中包含相互依賴的特徵有兩種方式，加強模型來表達輸入資料之前的關聯，或者簡單的做獨立性假設，比如樸素貝葉斯假設，第一種方法通常很難在提高模型複雜度的同時仍然保持模型優化的簡便，比如我們很難建立詞性和詞的字尾之間的關係，而實際上我們也不是特別願意去這麼做，第二種方法，對輸入資料做獨立性假設會使得準確性降低，儘管樸素貝葉斯在文字分類應用中表現出其的好，但是在很多其他的應用中都比邏輯迴歸要遜色雖然樸素貝葉斯的分類準確率較高，但是在概率估計應用方便表現較差。

對於CRF，我們給出準確的數學語言描述：

　　設X與Y是隨機變數，P(Y|X)是給定X時Y的條件概率分佈，若隨機變數Y構成的是一個馬爾科夫隨機場，則稱條件概率分佈P(Y|X)是條件隨機場。

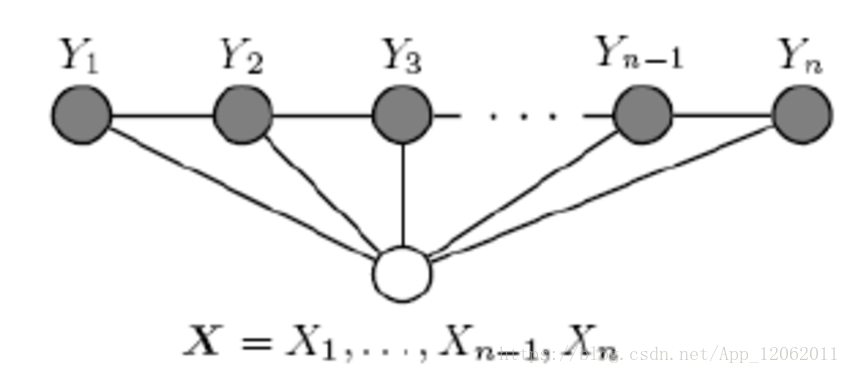
注意在CRF的定義中，我們並沒有要求X和Y有相同的結構。而實現中，我們一般都假設X和Y有相同的結構，即:

我們一般考慮如下圖所示的結構：X和Y有相同的結構的CRF就構成了線性鏈條件隨機場(Linear chain Conditional Random Fields,以下簡稱 linear-CRF)。

我們再來看看 linear-CRF的數學定義：

設 X=(X1,X2,...Xn),Y=(Y1,Y2,...Yn)均為線性連結串列示的隨機變數序列，在給定隨機變數序列X的情況下，隨機變數Y的條件概率分佈P(Y|X)構成條件隨機場，即滿足馬爾科夫性：

 則稱P(Y|X)為線性鏈條件隨機場。　

我們如何將其轉化為可以學習的機器學習模型呢？這是通過特徵函式和其權重係數來定義的。什麼是特徵函式呢？

在linear-CRF中，特徵函式分為兩類，第一類是定義在Y節點上的節點特徵函式，這類特徵函式只和當前節點有關，記為：

其中L是定義在該節點的節點特徵函式的總個數，i是當前節點在序列的位置。

第二類是定義在Y上下文的區域性特徵函式，這類特徵函式只和當前節點和上一個節點有關，記為：

其中K是定義在該節點的區域性特徵函式的總個數，i是當前節點在序列的位置。之所以只有上下文相關的區域性特徵函式，沒有不相鄰節點之間的特徵函式，是因為我們的linear-CRF滿足馬爾科夫性。

　　無論是節點特徵函式還是區域性特徵函式，它們的取值只能是0或者1。即滿足特徵條件或者不滿足特徵條件。同時，我們可以為每個特徵函式賦予一個權值，用以表達我們對這個特徵函式的信任度。假設tk的權重係數是λk,sl的權重係數是μl,則linear-CRF由我們所有的tk,λk,sl,μl共同決定。

　此時我們得到了linear-CRF的引數化形式如下(其實這裡看出，還是類似MaxEnt,SoftMax，多元邏輯迴歸模型)：

　其中，Z(x)為規範化因子：

回到特徵函式本身，每個特徵函式定義了一個linear-CRF的規則，則其係數定義了這個規則的可信度。所有的規則和其可信度一起構成了我們的linear-CRF的最終的條件概率分佈。

再次整理特徵函式，統一表示特徵。

假設我們在某一節點我們有K1個區域性特徵函式和K2個節點特徵函式，總共有K=K1+K2個特徵函式。我們用一個特徵函式fk(yi−1,yi,x,i)來統一表示如下:

對fk(yi−1,yi,x,i)在各個序列位置求和得到：

同時我們也統一fk(yi−1,yi,x,i)對應的權重係數wk如下：

這樣，我們的linear-CRF的引數化形式簡化為：

其中，Z(x)為規範化因子：

如果將上兩式中的wk與fk的用向量表示，即:

則linear-CRF的引數化形式簡化為內積形式如下：

我們還可以將linear-CRF的引數化形式寫成矩陣形式。為此我們定義一個m×m的矩陣M ，m為y所有可能的狀態的取值個數。M定義如下：

我們引入起點和終點標記y0=start,yn+1=stop, 這樣，標記序列y的非規範化概率可以通過n+1個矩陣元素的乘積得到，即： 

其中Zw(x)為規範化因子。

linear-CRF的三個基本問題

　　　　在HMM中，我們講到了HMM的三個基本問題，而linear-CRF也有三個類似的的基本問題。不過和HMM不同，在linear-CRF中，我們對於給出的觀測序列x是一直作為一個整體看待的，也就是不會拆開看(x1,x2,...)，因此linear-CRF的問題模型要比HMM簡單一些，如果你很熟悉HMM，那麼CRF的這三個問題的求解就不難了。

　　　　 linear-CRF第一個問題是評估，即給定 linear-CRF的條件概率分佈P(y|x), 在給定輸入序列x和輸出序列y時，計算條件概率P(yi|x)和P(yi−1，yi|x)以及對應的期望. 本文接下來會詳細討論問題一。

　　　　 linear-CRF第二個問題是學習，即給定訓練資料集X和Y，學習linear-CRF的模型引數wk和條件概率Pw(y|x)，這個問題的求解比HMM的學習演算法簡單的多，普通的梯度下降法，擬牛頓法都可以解決。

　　　　 linear-CRF第三個問題是解碼，即給定 linear-CRF的條件概率分佈P(y|x),和輸入序列x, 計算使條件概率最大的輸出序列y。類似於HMM，使用維特比演算法可以很方便的解決這個問題。

評估：

要計算條件概率P(yi|x)和P(yi−1，yi|x)，我們也可以使用和HMM類似的方法，使用前向後向演算法來完成。首先我們來看前向概率的計算。

　　　　我們定義αi(yi|x)表示序列位置i的標記是yi時，在位置i之前的部分標記序列的非規範化概率。之所以是非規範化概率是因為我們不想加入一個不影響結果計算的規範化因子Z(x)在分母裡面。我們還是引用之前的矩陣形式：

這個式子定義了在給定yi−1時，從yi−1轉移到yi的非規範化概率。也就是轉移概率（非歸一化）。

　　　　這樣，我們很容易得到序列位置i+1的標記是yi+1時，在位置i+1之前的部分標記序列的非規範化概率αi+1(yi+1|x)的遞推公式：

在起點處，我們定義：

假設我們可能的標記總數是m, 則yi的取值就有m個，我們用αi(x)表示這m個值組成的前向向量如下：

同時用矩陣Mi(x)表示由Mi(yi−1,yi|x)形成的m×m階矩陣：

　這樣遞推公式可以用矩陣乘積表示：

同樣的。我們定義βi(yi|x)表示序列位置i的標記是yi時，在位置i之後的從i+1到n的部分標記序列的非規範化概率。

　　　　這樣，我們很容易得到序列位置i+1的標記是yi+1時，在位置i之後的部分標記序列的非規範化概率βi(yi|x)的遞推公式：

在終點處，我們定義：

　如果用向量表示，則有：

由於規範化因子Z(x)的表示式是：

也可以用向量來表示Z(x):

其中，1是m維全1向量。

　有了前向後向概率的定義和計算方法，我們就很容易計算序列位置i的標記是yi時的條件概率P(yi|x):

也容易計算序列位置i的標記是yi，位置i−1的標記是yi−1時的條件概率P(yi−1,yi|x):

我們也可以很方便的計算聯合分佈P(x,y)P(x,y)與條件分佈P(y|x)P(y|x)的期望。

特徵函式fk(x,y)關於條件分佈P(y|x)的期望表示式是：

同樣可以計算聯合分佈P(x,y)的期望：

假設一共有K個特徵函式，則k=1,2,...K

訓練：

在linear-CRF模型引數學習問題中，我們給定訓練資料集X和對應的標記序列Y，K個特徵函式fk(x,y)，需要學習linear-CRF的模型引數wk和條件概率Pw(y|x)，其中條件概率Pw(y|x)和模型引數wk滿足一下關係：

所以我們的目標就是求出所有的模型引數wk，這樣條件概率Pw(y|x)Pw(y|x)可以從上式計算出來。

　　　　求解這個問題有很多思路，比如梯度下降法，牛頓法，擬牛頓法。同時，這個模型中Pw(y|x)的表示式和最大熵模型原理小結中的模型一樣，也可以使用最大熵模型中使用的改進的迭代尺度法(improved iterative scaling, IIS)來求解。

　　　　說白了，就是極大似然估計問題，不再贅述。

解碼：

在這個問題中，給定條件隨機場的條件概率P(y|x)和一個觀測序列x,要求出滿足P(y|x)最大的序列y。

　　　　這個解碼演算法最常用的還是和HMM解碼類似的維特比演算法。

　　　　維特比演算法本身是一個動態規劃演算法，利用了兩個區域性狀態和對應的遞推公式，從區域性遞推到整體，進而得解。對於具體不同的問題，僅僅是這兩個區域性狀態的定義和對應的遞推公式不同而已。由於在之前已詳述維特比演算法，這裡就是做一個簡略的流程描述。

　　　　對於我們linear-CRF中的維特比演算法，我們的第一個區域性狀態定義為δi(l),表示在位置i標記l各個可能取值(1,2...m)對應的非規範化概率的最大值。之所以用非規範化概率是，規範化因子Z(x)不影響最大值的比較。根據δi(l)的定義，我們遞推在位置i+1標記l的表示式為：

和HMM的維特比演算法類似，我們需要用另一個區域性狀態Ψi+1(l)來記錄使δi+1(l)達到最大的位置i的標記取值,這個值用來最終回溯最優解，Ψi+1(l)的遞推表示式為：

現在我們總結下 linear-CRF模型維特比演算法流程：

　　　　輸入：模型的K個特徵函式，和對應的K個權重。觀測序列x=(x1,x2,...xn)，可能的標記個數m

　　　　輸出：最優標記序列y∗=(y∗1,y∗2,...y∗n)

　　　　1) 初始化：

2) 對於i=1,2...n−1,進行遞推：

3) 終止：

4)回溯：

最終得到最優標記序列y∗=(y∗1,y∗2,...y∗n)

linear-CRF模型和HMM模型有很多相似之處，尤其是其三個典型問題非常類似，除了模型引數學習的問題求解方法不同以外，概率估計問題和解碼問題使用的演算法思想基本也是相同的。同時，兩者都可以用於序列模型，因此都廣泛用於自然語言處理的各個方面。

　　　　現在來看看兩者的不同點。最大的不同點是linear-CRF模型是判別模型，而HMM是生成模型，即linear-CRF模型要優化求解的是條件概率P(y|x),則HMM要求解的是聯合分佈P(x,y。第二，linear-CRF是利用最大熵模型的思路去建立條件概率模型，對於觀測序列並沒有做馬爾科夫假設。而HMM是在對觀測序列做了馬爾科夫假設的前提下建立聯合分佈的模型。

　　　　最後想說的是，只有linear-CRF模型和HMM模型才是可以比較討論的。但是linear-CRF是CRF的一個特例，CRF本身是一個可以適用於很複雜條件概率的模型，因此理論上CRF的使用範圍要比HMM廣泛的多。

模型比較

優點：
（1）和HMM相比，CRF直接對後驗概率建模，因而可以容納任意的上下文資訊。特徵設計靈活，
（2）和MEMM相比，由於CRF計算全域性最優輸出節點的條件概率，MEMM只是由前一個狀態轉移的狀態進行的歸一，而是對序列的所有可能組合進行歸一，克服了最大熵馬爾可夫模型標記偏置（Label-bias）的缺點
（3）和ME相比，CRF是在給定需要標記的觀察序列的條件下，計算整個標記序列的聯合概率分佈，考慮標號序列之間的關係，而不是把假設標註之間獨立，意思就是說，單獨的ME(MaxEnt)不能用做序列分類，而HMM,MEMM,CRF可以看成是序列分類，不是單獨詞分類。
缺點：訓練代價大、複雜度高

4.訓練補充
通過一組樣本，我們希望能夠得到CRF對應的分佈形式，並且用這種分佈形式對測試樣本進行分類。也就是測試樣本中每個隨機變數的取值。
在實際應用中，clique-potential主要由使用者自己定義的特徵函式組成，即使用者自己定義一組函式，這些函式被認為是可以用來幫助描述隨機變數分佈的。而這些特徵函式的強弱以及正向、負向是通過訓練得到的一組權重來表達的，這樣，實際應用中我們需要給出特徵函式以及權重的共享關係(不同的特徵函式可能共享同一個權重),而clicque-potential本質上成了對應特徵函式的線性組合。這些權重就成了CRF的引數。因此，本質上，圖的結構是使用者通過給出特徵函式的定義確定的（例如，只有一維特徵函式，對應的圖上是沒有邊的)還有，CRF的分佈成了對數線性形式。
看到這個分佈形式，我們自然會想到用最大似然準則來進行訓練。對其取log之後，會發現，表示式是convex的，也就是具有全域性最優解——這是很讓人振奮的事情。而且，其梯度具有解析解，這樣可以用LBFGS來求解極值。
此外，也可以使用最大熵準則進行訓練，這樣可以用比較成熟的GIS和IIS演算法進行訓練。由於對數線性的分佈形式下，最大熵準則和最大似然準則本質上是一樣的，所以兩者區別不是很大（好吧，三年後，我才真正理解這句話）。
此外，由於前面兩種訓練方法在每一輪迭代時，都需要inference,這樣會極大地降低訓練速度。因此普遍採用另一種近似的目標函式，稱為偽似然。它用每個隨機變數的條件分佈(就是給定其他所有隨件變數的分佈)之積來替代原來的似然函式，根據markov性質，這個條件分佈只和其鄰居有關(Markov Blanket),這樣在迭代過程中不需要進行全域性的inference,速度會得到極大的提升。我自己的經驗表明，當特徵函式很多取實數值時，偽似然的效果跟最大似然的差不多，甚至略好於後者。但對於大量二元特徵(binary-valued)，偽似然的效果就很差了。
5.推斷
如前所述，訓練的過程中我們需要概率推斷，分類的時候我們需要找出概率最大的一組解，這都涉及到推斷。這個問題本質上屬於圖模型上的概率推斷問題。對於最簡單的線性框架的結構，我們可以使用Viterbi演算法。如果圖結果是樹形的，可以採用信念傳播(belief propogation),用sum-product得到概率，用max-product得到最優的configuration.但是對於任意圖，這些方法就無效了。一種近似的演算法，稱為loopy-belief propogation,就是在非樹形結構上採用信念傳播來進行推斷，通過迴圈傳播來得到近似解。這麼做據說在某些場合下效果不錯。但是，在訓練時如果採用近似推斷的話，可能會導致長時間無法收斂。
基於任意圖上的概率推斷演算法稱為 junction  tree。這個演算法能夠保證對任意圖進行精確推理。它首先把原來的圖進行三角化，在三角化的圖上把clique按照某種方式枚舉出來作為節點（實際上就是合併特徵函式),clicque之間如果有交集，對應的節點之間就有邊，這樣就得到一個新的圖，通過對這個圖求最大生成樹，就得到了Junction tree. 最後在junction tree上進行信念傳播可以保證得到精確解。
本質上這3中演算法都屬於動態規劃的思想。Viterbi的想法最直觀，信念傳播首先將特徵函式都轉換為factor，並將其與隨機變數組合在一起形成 factor-graph, 這樣在factor-graph上用動態規劃的思想進行推斷（即做了一些預處理)。junction tree的做法是通過合併原有的特徵函式, 形成一種新的圖，在這個圖上可以保證動態規劃的無後效性，於是可以進行精確推理。(做了更為複雜的預處理)
值得注意的是，junction tree雖然極大地避開了組合爆炸，但由於它要合併特徵函式並尋找clique, 使用者的特徵函式如果定義的維數過大，它得到新的clique也會很大，這樣在計算的時候還是會很低效，因為在推斷的過程中它需要遍歷所有clique中的配置，這和clique的大小是呈指數級的。所以，使用者要避免使用維數過高的特徵。

與其他演算法的比較

優點：

（1）CRF沒有HMM那樣嚴格的獨立性假設條件，因而可以容納任意的上下文資訊。特徵設計靈活（與ME一樣）————與HMM比較

（2）同時，由於CRF計算全域性最優輸出節點的條件概率，它還克服了最大熵馬爾可夫模型標記偏置（Label-bias）的缺點。­­————與MEMM比較

（3）CRF是在給定需要標記的觀察序列的條件下，計算整個標記序列的聯合概率分佈，而不是在給定當前狀態條件下，定義下一個狀態的狀態分佈。

­­ ————與ME比較

缺點：訓練代價大、複雜度高

HMM,MEMM,CRF模型的比較

這三個模型都可以用來做序列標註模型。但是其各自有自身的特點，HMM模型是對轉移概率和表現概率直接建模，統計共現概率。而MEMM模型是對轉移概率和表現概率建立聯合概率，統計是統計的是條件概率。MEMM容易陷入區域性最優，是因為MEMM只在區域性做歸一化，而CRF模型中，統計了全域性概率，在做歸一化時，考慮了資料在全域性的分佈，而不是僅僅在區域性歸一化，這樣就解決了MEMM中的標記偏置的問題。

舉個例子，對於一個標註任務，“我愛北京天安門“，

                                  標註為" s s  b  e b c e"

對於HMM的話，其判斷這個標註成立的概率為 P= P(s轉移到s)*P('我'表現為s)* P(s轉移到b)*P('愛'表現為s)* ...*P().訓練時，要統計狀態轉移概率矩陣和表現矩 陣。

對於MEMM的話，其判斷這個標註成立的概率為 P= P(s轉移到s|'我'表現為s)*P('我'表現為s)* P(s轉移到b|'愛'表現為s)*P('愛'表現為s)*..訓練時，要統計條件狀態轉移概率矩陣和表現矩陣。

對於CRF的話，其判斷這個標註成立的概率為 P= F(s轉移到s,'我'表現為s)....F為一個函式，是在全域性範圍統計歸一化的概率而不是像MEMM在區域性統計歸一化的概率。

機器學習方法的兩種分類：產生式模型和判別式模型
假定輸入x, 類別標籤y
—產生式模型（生成模型）估計聯合概率 P(x, y), 因可以根據聯合概率來生成樣本 —: HMMs
—判別式模型（判別模型）估計條件概率 P(y|x), 因為沒有x的知識，無法生成樣本，只能判斷分類: SVMs,CRF,MEM
一個舉例：
(1,0), (1,0), (2,0), (2, 1)
產生式模型：

p(x, y)：
P(1, 0) = 1/2, P(1, 1) = 0, P(2, 0) = 1/4, P(2, 1) = 1/4.

判別式模型：
P(y|x)：
P(0|1) = 1, P(1|1) = 0, P(0|2) = 1/2, P(1|2) = 1/2
—o和s分別代表觀察序列和標記序列
—產生式模型
—     構建o和s的聯合分佈p(s,o)
—判別式模型
—     構建o和s的條件分佈p(s|o)
—產生式模型中，觀察序列作為模型的一部分；
—判別式模型中，觀察序列只作為條件，因此可以針對觀察序列設計靈活的特徵。
產生式模型：無窮樣本==》概率密度模型 = 產生模型==》預測
判別式模型：有限樣本==》判別函式 = 預測模型==》預測
    一般認為判別型模型要好於生成型模型，因為它是直接根據資料對概率建模，而生成型模型還要先求兩個難度相當的概率

補充下標記偏置問題：

原文：http://blog.csdn.net/zhoubl668/article/details/7787690

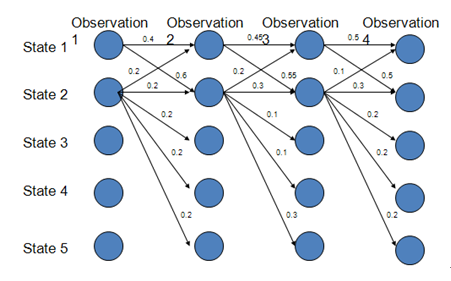
路徑1-1-1-1的概率：0.4*0.45*0.5=0.09

路徑2-2-2-2的概率:0.018

路徑1-2-1-2:0.06

路徑1-1-2-2:0.066

由此可得最優路徑為1-1-1-1

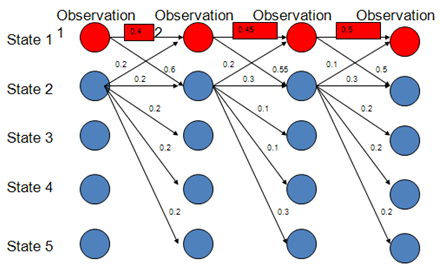
而實際上，在上圖中，狀態1偏向於轉移到狀態2，而狀態2總傾向於停留在狀態2，這就是所謂的標註偏置問題，由於分支數不同，概率的分佈不均衡，導致狀態的轉移存在不公平的情況。

PS：標註偏置問題存在於最大熵馬爾可夫模型（MEMM）中，雖然MEMM解決了HMM輸出獨立性假設的問題，但是隻解決了觀察值獨立的問題，狀態之間的假設則是標註偏置問題產生的根源，CRF則解決了標註偏置問題，是HMM模型的進一步優化。

HMM模型中存在兩個假設：一是輸出觀察值之間嚴格獨立，二是狀態的轉移過程中當前狀態只與前一狀態有關(一階馬爾可夫模型)。

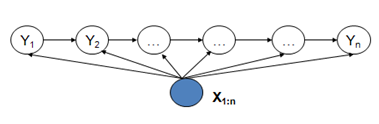
MEMM模型克服了觀察值之間嚴格獨立產生的問題，但是由於狀態之間的假設理論，使得該模型存在標註偏置問題。

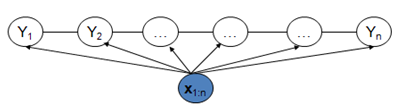
CRF模型解決了標註偏置問題，去除了HMM中兩個不合理的假設，當然，模型相應得也變複雜了。

幾種統計模型對比：

HMM模型將標註看作馬爾可夫鏈，一階馬爾可夫鏈式針對相鄰標註的關係進行建模，其中每個標記對應一個概率函式。HMM是一種產生式模型，定義了聯合概率分佈 ，其中x和y分別表示觀察序列和相對應的標註序列的隨機變數。為了能夠定義這種聯合概率分佈，產生式模型需要枚舉出所有可能的觀察序列，這在實際運算過程中很困難，因為我們需要將觀察序列的元素看做是彼此孤立的個體即假設每個元素彼此獨立，任何時刻的觀察結果只依賴於該時刻的狀態。

HMM模型的這個假設前提在比較小的資料集上是合適的，但實際上在大量真實語料中觀察序列更多的是以一種多重的互動特徵形式表現，觀察元素之間廣泛存在長程相關性。在命名實體識別的任務中，由於實體本身結構所具有的複雜性，利用簡單的特徵函式往往無法涵蓋所有的特性，這時HMM的假設前提使得它無法使用複雜特徵(它無法使用多於一個標記的特徵。

最大熵模型可以使用任意的複雜相關特徵，在效能上最大熵分類器超過了Byaes分類器。但是，作為一種分類器模型，這兩種方法有一個共同的缺點：每個詞都是單獨進行分類的，標記之間的關係無法得到充分利用，具有馬爾可夫鏈的HMM模型可以建立標記之間的馬爾可夫關聯性，這是最大熵模型所沒有的。

最大熵模型的優點：首先，最大熵統計模型獲得的是所有滿足約束條件的模型中資訊熵極大的模型;其次，最大熵統計模型可以靈活地設定約束條件，通過約束條件的多少可以調節模型對未知資料的適應度和對已知資料的擬合程度;再次，它還能自然地解決了統計模型中引數平滑的問題。

最大熵模型的不足：首先，最大熵統計模型中二值化特徵只是記錄特徵的出現是否，而文字分類需要知道特徵的強度，因此，它在分類方法中不是最優的;其次，由於演算法收斂的速度較慢，所以導致最大熵統計模型它的計算代價較大，時空開銷大;再次，資料稀疏問題比較嚴重。

最大熵馬爾科夫模型把HMM模型和maximum-entropy模型的優點集合成一個產生式模型，這個模型允許狀態轉移概率依賴於序列中彼此之間非獨立的特徵上，從而將上下文資訊引入到模型的學習和識別過程中，提高了識別的精確度，召回率也大大的提高，有實驗證明，這個新的模型在序列標註任務上表現的比HMM和無狀態的最大熵模型要好得多。

CRF模型的特點：首先，CRF在給定了觀察序列的情況下，對整個的序列的聯合概率有一個統一的指數模型。一個比較吸引人的特性是其 損失函式 的凸面性。其次，條件隨機域模型相比較改進的隱馬爾可夫模型可以更好更多的利用待識別文字中所提供的上下文資訊以得更好的實驗結果。條件隨機域在中文組塊識別方面有效，並避免了嚴格的獨立性假設和資料歸納偏置問題。條件隨機域(CRF)模型應用到了中文名實體識別中，並且根據中文的特點，定義了多種特徵模板。並且有測試結果表明：在採用相同特徵集合的條件下，條件隨機域模型較其他概率模型有更好的效能表現。再次，詞性標註主要面臨兼類詞消歧以及未知詞標註的難題，傳統隱馬爾科夫方法不易融合新特徵，而最大熵馬爾科夫模型存在標註偏置等問題。論文引入條件隨機域建立詞性標註模型，易於融合新的特徵，並能解決標註偏置的問題。

CRFs具有很強的推理能力，並且能夠使用複雜、有重疊性和非獨立的特徵進行訓練和推理，能夠充分地利用上下文資訊作為特徵，還可以任意地新增其他外部特徵，使得模型能

夠獲取的資訊非常豐富。同時，CRFs解決了最大熵模型中的“label bias”問題。CRFs與最大熵模型的本質區別是：最大熵模型在每個狀態都有一個概率模型，在每個狀態轉移時都要進行歸一化。如果某個狀態只有一個後續狀態，那麼該狀態到後續狀態的跳轉概率即為1。這樣，不管輸入為任何內容，它都向該後續狀態跳轉。而CRFs是在所有的狀態上建立一個統一的概率模型，這樣在進行歸一化時，即使某個狀態只有一個後續狀態，它到該後續狀態的跳轉概率也不會為1，從而解決了“labelbias”問題。因此，從理論上講，CRFs非常適用於中文的詞性標註。

      CRF模型的優點：首先，CRF模型由於其自身在結合多種特徵方面的優勢和避免了標記偏置問題。其次，CRF的效能更好，CRF對特徵的融合能力比較強，對於例項較小的時間類ME來說，CRF的識別效果明顯高於ME的識別結果。

      CRF模型的不足：首先，通過對基於CRF的結合多種特徵的方法識別英語命名實體的分析，發現在使用CRF方法的過程中，特徵的選擇和優化是影響結果的關鍵因素，特徵選擇問題的好與壞，直接決定了系統性能的高低。其次，訓練模型的時間比ME更長，且獲得的模型很大，在一般的PC機上無法執行。

再補充一點：

實際上，網上大多數資料中CRF主要用在詞性標註問題上，也就是解碼過程。