五種典型的遞推關係——一步一步演算法篇
五種典型的遞推關係
1.Fibonacci數列
在所有的遞推關係中,Fibonacci數列應該是最為大家所熟悉的。在最基礎的程式設計語言Logo語言中,就有很多這類的題目。而在較為複雜的Basic、Pascal、C語言中,Fibonacci數列類的題目因為解法相對容易一些,逐漸退出了競賽的舞臺。可是這不等於說Fibonacci數列沒有研究價值,恰恰相反,一些此類的題目還是能給我們一定的啟發的。
Fibonacci數列的代表問題是由義大利著名數學家Fibonacci於1202年提出的“兔子繁殖問題”(又稱“Fibonacci問題”)。
問題的提出:有雌雄一對兔子,假定過兩個月便可繁殖雌雄各一的一對小兔子。問過n個月後共有多少對兔子?
解
Fx=Nx+ Fx-1
Nx=Fx-2 (即第x-2個月的所有兔子到第x個月都有繁殖能力)
∴ Fx=Fx-1+Fx-2 邊界條件:F0=0,F1=1
由上面的遞推關係可依次得到:
F2=F1+F0=1,F3=F2+F1=2,F4=F3+F2=3,F5=F4+F3=5,……。
Fabonacci數列常出現在比較簡單的組合計數問題中,例如以前的競賽中出現的“骨牌覆蓋”問題。在優選法中,Fibonacci數列的用處也得到了較好的體現。
2.Hanoi塔問題
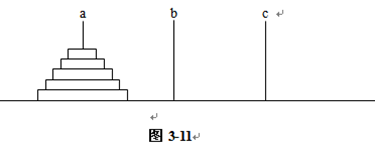
問題的提出:Hanoi塔由n個大小不同的圓盤和三根木柱a,b,c組成。開始時,這n個圓盤由大到小依次套在a柱上,如圖3-11所示。
要求把a柱上n個圓盤按下述規則移到c柱上:
(1)一次只能移一個圓盤;
(2)圓盤只能在三個柱上存放;
(3)在移動過程中,不允許大盤壓小盤。
問將這n個盤子從a柱移動到c柱上,總計需要移動多少個盤次?
解:設hn為n個盤子從a柱移到c柱所需移動的盤次。顯然,當n=1時,只需把a 柱上的盤子直接移動到c柱就可以了,故h1=1。當n=2時,先將a柱上面的小盤子移動到b柱上去;然後將大盤子從a柱移到c 柱;最後,將b柱上的小盤子移到c柱上,共記3個盤次,故h2=3。以此類推,當a柱上有n(n2)個盤子時,總是先借助c柱把上面的n-1個盤子移動到b柱上,然後把a柱最下面的盤子移動到c柱上;再借助a柱把b柱上的n-1個盤子移動到c柱上;總共移動hn-1+1+hn-1個盤次。
∴hn=2hn-1+1 邊界條件:h1=1
3.平面分割問題
問題的提出:設有n條封閉曲線畫在平面上,而任何兩條封閉曲線恰好相交於兩點,且任何三條封閉曲線不相交於同一點,問這些封閉曲線把平面分割成的區域個數。
解:設an為n條封閉曲線把平面分割成的區域個數。 由圖3-13可以看出:a2-a1=2;a3-a2=4;a4-a3=6。
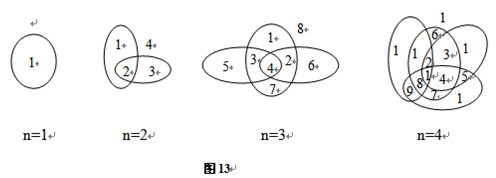
從這些式子中可以看出an-an-1=2(n-1)。當然,上面的式子只是我們通過觀察4幅圖後得出的結論,它的正確性尚不能保證。下面不妨讓我們來試著證明一下。當平面上已有n-1條曲線將平面分割成an-1個區域後,第n-1條曲線每與曲線相交一次,就會增加一個區域,因為平面上已有了n-1條封閉曲線,且第n條曲線與已有的每一條閉曲線恰好相交於兩點,且不會與任兩條曲線交於同一點,故平面上一共增加2(n-1)個區域,加上已有的an-1個區域,一共有an-1+2(n-1)個區域。所以本題的遞推關係是an=an-1+2(n-1),邊界條件是a1=1。
平面分割問題是競賽中經常觸及到的一類問題,由於其靈活多變,常常感到棘手,下面的例8是另一種平面分割問題,有興趣的讀者不妨自己先試著求一下其中的遞推關係。
4.Catalan數
Catalan數首先是由Euler在精確計算對凸n邊形的不同的對角三角形剖分的個數問題時得到的,它經常出現在組合計數問題中。
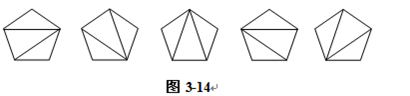
問題的提出:在一個凸n邊形中,通過不相交於n邊形內部的對角線,把n邊形拆分成若干三角形,不同的拆分數目用hn表示,hn即為Catalan數。例如五邊形有如下五種拆分方案(圖3-14),故h5=5。求對於一個任意的凸n邊形相應的hn。
Catalan數是比較複雜的遞推關係,尤其在競賽的時候,選手很難在較短的時間裡建立起正確的遞推關係。當然,Catalan數類的問題也可以用搜索的方法來完成,但是,搜尋的方法與利用遞推關係的方法比較起來,不僅效率低,程式設計複雜度也陡然提高。
第二類Stirling數
在五類典型的遞推關係中,第二類Stirling是最不為大家所熟悉的。也正因為如此,我們有必要先解釋一下什麼是第二類Strling數。
**【定義2】**n個有區別的球放到m個相同的盒子中,要求無一空盒,其不同的方案數用S(n,m)表示,稱為第二類Stirling數。
下面就讓我們根據定義來推導帶兩個引數的遞推關係——第二類Stirling數。
解:設有n個不同的球,分別用b1,b2,……bn表示。從中取出一個球bn,bn的放法有以下兩種:
①bn獨自佔一個盒子;那麼剩下的球只能放在m-1個盒子中,方案數為S2(n-1,m-1);
②bn與別的球共佔一個盒子;那麼可以事先將b1,b2,……bn-1這n-1個球放入m個盒子中,然後再將球bn可以放入其中一個盒子中,方案數為mS2(n-1,m)。
綜合以上兩種情況,可以得出第二類Stirling數定理:
【定理】S2(n,m)=mS2(n-1,m)+S2(n-1,m-1) (n>1,m1)
邊界條件可以由定義2推匯出:
S2(n,0)=0;S2(n,1)=1;S2(n,n)=1;S2(n,k)=0(k>n)。
第二類Stirling數在競賽中較少出現,但在競賽中也有一些題目與其類似,甚至更為複雜。讀者不妨自己來試著建立其中的遞推關係。
小結:通過上面對五種典型的遞推關係建立過程的探討,可知對待遞推類的題目,要具體情況具體分析,通過找到某狀態與其前面狀態的聯絡,建立相應的遞推關係。
一步一步演算法篇
相關推薦
五種典型的遞推關係——一步一步演算法篇
五種典型的遞推關係 1.Fibonacci數列 在所有的遞推關係中,Fibonacci數列應該是最為大家所熟悉的。在最基礎的程式設計語言Logo語言中,就有很多這類的題目。而在較為複雜的Basic、Pascal、C語言中,Fibonacci數列類的題
【POJ1958】【典型遞推問題】漢諾塔問題
題意: 給你n個盤子,問在四個柱子的情況下,最少需要多少步才能將n個盤子移動到另一個柱子上。 思路: 先來看看最經典的三個柱子問題。 f3[
五種典型開發週期模型(瀑布、V、原型化、螺旋、迭代)
總結一下經常可以見到的系統開發週期模型。 在過去的幾年裡,可以很奇葩的碰到類似於“創業專案庫”這種需求非常明確,工作量十分可控,對質量要求比較低,業務建模比較easy,功能構成比較少的“面子專案”。類似於這種專案,採用傳統意義上的瀑布模型就非常合適了,如果範圍控制和風險控制做的比較好的話,真的如
軟體工程五種典型的開發模型各自特點----阿冬專欄
轉自:http://www.cnblogs.com/kzloser/archive/2012/07/06/2578835.html 瀑布模型 1.里程碑或基線驅動。2.過程逆轉性很差或者說不可逆轉。逆轉可能會延誤工期,增加成本,造成損失 1.開發階段清晰,便
總結一下五種實現網路爬蟲的方法(一,基於socket通訊編寫爬蟲)
最近呢,由於實習需要呢,複習一遍爬蟲,前斷時間閉關刷題去了,也會把刷題心得總結成部落格分享給大家,比如java集合類特性及原始碼解析,作業系統資料結構的一些演算法,設計模式等,放心,肯定不會鴿的,雖然可能會晚一點寫。言歸正傳,java實現網路爬蟲一般有五種方法(據我所知,要是
矩陣快速冪在常係數線性遞推關係中的應用
先引入一下,知乎上有一個問題 關於斐波拉契數列的一個低階問題 。題主詢問了關於求解斐波拉契數列第n項對10007取模的結果。而這個n,可以達到106甚至109 。 解法已經在排名第一的回答中給出了,主要思路就是快速冪和矩陣乘法的結合律,亦即矩陣快速冪。具體方法
【演算法】幾個經典遞推關係記錄
遞推關係數學味很重(貌似很多都是直接有公式的),不過很多記憶搜尋或者dp的狀態轉移都是要自己推理的,記錄幾個俗爆炸的遞推關係... 文科生學計算機......我呵呵一臉 :( Fibonacci 這個很常見,第一次刷題愣是沒找出來...覺得特難(文科生的悲哀)! 目前
hdu step 3 1 1 超級樓梯 簡單遞推 從第1級到第m級有多少種走法 每次只能走一步或兩步
在寫題解之前給自己打一下廣告哈~。。抱歉了,希望大家多多支援我在CSDN的視訊課程,地址如下:http://edu.csdn.net/course/detail/209題目:超級樓梯Time Limit: 2000/1000 MS (Java/Others) Memory Li
一種遞推組合數字首和的Trick
記錄一下一種推組合數字首和的方法 ## Trick 設$\sum_{i = 0}^m C_n^i = S(n, m)$ $S$是可以遞推的 - $S(n, m + 1) = S(n, m) + C_{n}^{m + 1}$ 就是加上最末尾的一項 - $S(n + 1, m)
51nod 1361 有一種遞推(一階二次遞推式)
矩陣 個數 bubuko 二次 技術 有一種 這就是 mage 9.png 分析:- - 這就是個數學競賽題啊...遞推式可以這麽求: tn可以用矩陣快速冪求出來,然後用最後一個式子求一下bn再代回去求an就行了。p^2-1不一定是最小周期,但一定是一個周期。51
c語言中一種典型的排列組合算法
scan .com nbsp 方法 can main else const 組合數 c語言中的全排列算法和組合數算法在實際問題中應用非常之廣,但算法有許許多多,而我個人認為方法不必記太多,最好只記熟一種即可,一招鮮亦可吃遍天 全排列: #include<stdio.h
由DAG到背包問題——記憶化搜索和遞推兩種解法
必須 結果 stream size 遞推 algo main style 得到 一、問題描述 物品無限的背包問題:有n種物品,每種均有無窮多個。第 i 種物品的體積為Vi,重量為Wi。選一些物品裝到一個容量為 C 的背包中,求使得背包內物品總體積不超過C的前提下重量的最大值
[ 9.26 ]CF每日一題系列—— 771B遞推問題
std ret 重名 () while 字數 har rip ace Description: 給定你命名的規律,1-10個字符,開頭必須大寫,最多有50個名字,然後告訴你有n個人,判斷區間長度為k,那麽你將得到n - k + 1個答案(YES or NO) 表示1 -
[神經網絡]一步一步使用Mobile-Net完成視覺識別(五)
arc del img fault model coord graph 處理 mobile 1.環境配置 2.數據集獲取 3.訓練集獲取 4.訓練 5.調用測試訓練結果 6.代碼講解 本文是第五篇,講解如何調用測試訓練結果。 上一篇中我們輸出了訓練的模型,這一篇中我們通
一隻小蜜蜂(hdoj 2044,動態規劃遞推)
Problem Description 有一隻經過訓練的蜜蜂只能爬向右側相鄰的蜂房,不能反向爬行。請程式設計計算蜜蜂從蜂房a爬到蜂房b的可能路線數。 其中,蜂房的結構如下所示。 Input 輸入資料的第一行是一個整數N,表示測試例項的個數,然後是N 行資料,每行包含兩個整
五種型別的程式設計師,你屬於哪一種?
在我的程式設計生涯中,我碰到過很多奇奇怪怪的對手和同盟。我把這些編碼戰士們分成五類,有些人是你隊伍中的好夥伴,有些人則是搗蛋者,讓你的每一個計劃都完不成。 不管怎麼說,他們在軟體開發的諸神殿上都佔有一席之地。如果你的團隊中沒有一個合適健康的比例,混合這些不同型別的程式設計師,要麼你會發現你的專案跌跌
《C++ Primer Plus》學習筆記——第五章 迴圈和關係表示式(一)
本章內容: for迴圈和while迴圈 表示式和語句 運算子組合 複合語句 逗號運算子以及關係運算符 typedef工具 字元輸入方法get() 檔案尾條件 巢狀迴圈和二維陣列 計算機除了儲存資料外,還可以做很多其他工作。可以對資料進
矩陣快速冪(共軛函式兩種遞推式)
題目連結:https://cn.vjudge.net/contest/261339#problem/B AC1:ans= x(n)+y(n)*sqrt(6),所以,ans=x(n)+y(n)*sqrt(6)+(x(n)-y(n)*sqrt(6))-(x(n)-y(n)*sqrt(6))=2*
Redis學習筆記(一)---Redis的五種資料型別的簡單介紹和使用
1.準備工作: 1.1在Linux下安裝Redis https://www.cnblogs.com/dddyyy/p/9763098.html 1.2啟動Redis 先把root/redis的redis.conf放到 /usr/local/redis/
JPA 五種 對映關係
一、JPA_對映單向多對一的關聯關係 1、建立實體類 //訂單 @Table(name="JPA_ORDER") @Entity public class Order { private Integer id; private String orderName; priva