題目背景

這是一道模板題

題目描述

給定n,p求1~n中所有整數在模p意義下的乘法逆元。

輸入輸出格式

輸入格式：

一行n,p

輸出格式：

n行,第i行表示i在模p意義下的逆元。

輸入輸出樣例

10 13

1
7
9
10
8
11
2
5
3
4

說明

1≤n≤3×10​6​​,n<p<20000528

輸入保證 p 為質數。

我們有三種辦法求逆元 

由尤拉定理可知 

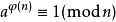
當gcd(a,n)==1 時 我們有 A^φ(n-1)≡ 1(mod n) ;

所以 我們有 A*A^φ(n-2) ≡ 1(mod n) 

所以A^φ(n-2) 就是A關於mod n的逆元 

 1 /*
 2     p為素數時 可用費馬小定理 
 3     longlong*longlong 要慢一點 66分 
 4 */
 5 #include <cctype>
 6 #include <cstdio>
 7 
 8 typedef long long LL;
 9 
10 int n,p;
11 
12 inline LL quick_pow(LL a,int k) {
13     LL ret=1;
14     while(k) {
15         if(k&1) ret=(ret*a)%p;
16         k>>=1
 
;
17         a=(a*a)%p;
18     }
19     return ret;
20 }
21 
22 int hh() {
23     scanf("%d%d",&n,&p);
24     printf("1\n");
25     for(int i=2;i<=n;++i) {
26         LL t=quick_pow(i,p-2);
27         printf("%d\n",(t+p)%p);
28     }
29     return 0;
30 }
31 
32 int sb=hh();
33 int main(int argc,char
 
**argv) {;}

還有我們可以用exgcd來求逆元 

我們知道 若ax≡1(mod p)  這我們可以寫成 ax=py+1；

移項則有 ax-by=1  這明顯就是擴充套件歐幾里得

當 ax+by=gcd(a,b)  gcd(a,b) == gcd(b,a%b) 

我們得到 bx1+(a-a/b)y1=gcd(b,a%b);

則 ax+by=bx1+(a-(a/b)*b)y1 //這裡 / 代表整除

   ax+by=bx1+ay1-b*(a/b)y1 

   ax+by=ay1+b(x1-(a/b)*y1) 

我們得到 x=y1

　　　　 y=x1-(a/b)*y1;

x 即為我們所求的逆元 

由於 x 可能為負數 要(x+p)%p 

 1 /*
 2     EXgcd 求逆元
 3     比費馬小定理要快一點 83分  
 4 */
 5 #include <cstdio>
 6 #include <cctype>
 7 
 8 int n,p;
 9 
10 inline int exgcd(int a,int b,int&x,int&y) {
11     if(!b) {
12         x=1;y=0;
13         return a;
14     }
15     int p=exgcd(b,a%b,x,y);
16     int t=x;
17     x=y;
18     y=t-(a/b)*y;
19     return p;
20 } 
21 
22 int hh() {
23     scanf("%d%d",&n,&p);
24     printf("1\n");
25     int x,y; 
26     for(int i=2;i<=n;++i) {
27         exgcd(i,p,x,y);
28         printf("%d\n",(x+p)%p);
29     }
30     return 0;
31 }
32 
33 int sb=hh();
34 int main(int argc,char**argv) {;}

但是對於 這個題來講 複雜度還是不夠 

我們還有線性求逆元的方法 

來看帶餘除法 式子 p=k*i+r 

我們可以寫成 k*i+r≡0(mod p) 

式子兩邊同乘 i^-1*r^-1 (i^-1,r^-1皆為模p意義下的逆元) 

所以我們有 k*r^-1+i^-1≡0(mod p) 

i^-1≡-k*r^-1(mod p)

i^-1≡-(p/i)*(p%i)^-1(mod p)

這樣我們就線性求得了逆元

 1 #include <cctype>
 2 #include <cstdio>
 3 
 4 typedef long long LL;
 5 const int MAXN=3000010;
 6 
 7 int n,p;
 8 
 9 LL inv[MAXN];
10 
11 int hh() {
12     scanf("%d%d",&n,&p);
13     printf("1\n");
14     inv[1]=1;
15     for(int i=2;i<=n;++i) {
16         inv[i]=(LL)(p-p/i)*inv[p%i]%p;
17         printf("%d\n",inv[i]);
18     }
19     return 0;
20 } 
21 
22 int sb=hh();
23 int main(int argc,char**argv) {;}