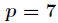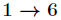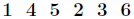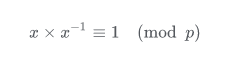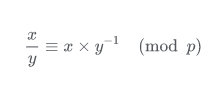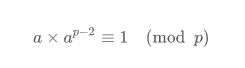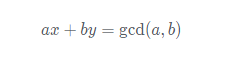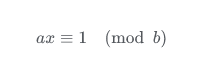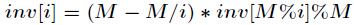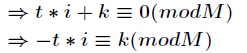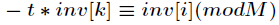乘法逆元的幾種計算方法
阿新 • • 發佈:2019-01-29
乘法逆元是數論中重要的內容,也是 ACM 中常用到的數論演算法之一。所以,如何高效的求出乘法逆元是一個值得研究的問題。
這裡我們只討論當模數為素數的情況,因為如果模數不為素數,則不一定每個數都有逆元。
定義
在 mod p的意義下我們把 x 的乘法逆元寫作 x−1。
乘法逆元有如下的性質:
乘法逆元的一大應用是模意義下的除法,除法在模意義下並不是封閉的,但我們可以根據上述公式,將其轉化為乘法。
費馬小定理

要求 p 為素數。
上述公式可變形為
由乘法逆元的定義,ap−2 即為 a 的乘法逆元。
使用快速冪計算 ap−2,總時間複雜度為 O(loga)。
程式碼
inline int pow(const int n, const int k) { long long ans = 1; for (long long num = n, t = k; t; num = num * num % MOD, t >>= 1) if (t & 1) ans = ans * num % MOD; return ans; } inline int inv(const int num) { return pow(num, MOD - 2); }
擴充套件歐幾里得
擴充套件歐幾里得(EXGCD)演算法可以在 O(logmax(a,b)) 的時間內求出關於 x、y 的方程
的一組整數解
當 b 為素數時,gcd(a,b)=1,此時有
時間複雜度為 O(loga)。
程式碼
void exgcd(const int a, const int b, int &g, int &x, int &y) { if (!b) g = a, x = 1, y = 0; else exgcd(b, a % b, g, y, x), y -= x * (a / b); } inline int inv(const int num) { int g, x, y; exgcd(num, MOD, g, x, y); return ((x % MOD) + MOD) % MOD; }
遞推法
程式碼
inv[1] = 1;
for (int i = 2; i <= MAXN; i++) inv[i] = ((-(MOD / i) * inv[MOD % i]) % MOD + MOD) % MOD;下面是ACdreamers關於遞推求解逆元的推導過程(個人覺得他的更好)
其實有些題需要用到


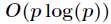
如果對於一個1000000級別的素數
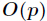
它的推導過程如下,設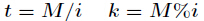
對上式兩邊同時除
再把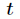
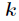
初始化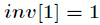


另外