上篇文章我們知道求解迷宮通路的方法，但是一個迷宮有時是不止一條出路，在這些出路中，我們如何找到最短的那一條，這就是我今天要說的迷宮最短路徑問題。

（此處使用的圖）：

【先來分析有什麼解決方案：】

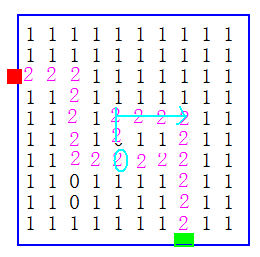
1、方法一：我們如果採用上章中遞迴的方式，將所走的路用2標記起來，此時如果找到一條路後，要進行回溯遞迴，但是到可以走的環中就出現問題了，說的有點迷糊是吧，我把圖丟擲來。

在這張圖中我們可以看到，如果我們遞迴到又有一個可以走的路，就是圓圈2，那麼上面藍色線指的就走不回去了，因為已經走過了。所以這種方法是不可取的。有這方面的缺陷。

2、方法二：還是利用遞迴，但是我們做法不同

1）、每走一步標記的數值加1
2）、利用遞迴進行探測
3）、當找到一條路的時候，回溯遞迴
4）、此時，當探測的位置可以通的話，就繼續走，將下一位置標記數值加1
（為了防止回去，原則就是不能走比他數值小的位置）

【我們就採用第二種方案，來看怎麼實現】：

#include<iostream>
#include<assert.h>
#include<stack>
using namespace std;
#define N 10
//const size_t N = 10;

//迷宮中所走的位置表示
struct Pos
{
   /* size_t*/ int _row;  //所在位置的行
	/*sizt_t*/int _col;  //所在位置的列
};

//獲取迷宮
void GetMaze(int* maze,size_t n)
{
	FILE* fp = fopen("2.txt","r");  //先通過相對路徑開啟儲存迷宮地圖的文字
	assert(fp);       //開啟文字是否成功
	for(size_t i = 0; i<n; i++)
	{
		for(size_t j = 0; j<n;)
		{
			int ret = fgetc(fp);
			if((ret == '0')|| (ret == '1'))
			{
				maze[i*n+j] = ret-'0';      //注意開啟的是文字要轉化成讀出的二進位制形式
				j++;
			}
			//如果迷宮地圖本身不是n*n的，那麼上面的迴圈就會成為死迴圈
			if(ret == EOF)
			{
				cout<<"出錯！"<<endl;
			}
		}
	}
}
//檢查此位置是否可以通
bool CheckIsAccess(int* maze,size_t n,Pos pos)
{
	//首先這個位置得合法，其次再是pos這個位置是否為0
	if(pos._row>=0 && pos._row<n &&
		pos._col>=0 && pos._col<n &&
		maze[pos._row*n+pos._col] == 0)
	{
		return true;
	}
	return false;
}
bool CheckIsAccess(int* maze,size_t n,Pos cur,Pos next)
{
	//首先要走的這個位置得合法
	if(next._row<=0 && next._row>n &&
		next._col<=0 && next._col>n &&
		maze[next._row*n+next._col] == 1)
	{
		return false;
	}
	//這個位置如果是0
	if(maze[next._row*n+next._col] == 0)
	{
		return true;
	}
	//下一個位置要大於上一個位置加1（原則）
	if(maze[next._row*n+next._col] > maze[cur._row*n+next._col]+1)
	{
		return true;
	}
	return false;
}
//求解迷宮路徑
void GetMazePath_r(int* maze,size_t n,Pos entry,stack<Pos>& path,stack<Pos>& shortpath)
{
	assert(maze);
	path.push(entry);
	Pos cur;    
	Pos next;
    cur = entry;
	maze[cur._row*n+cur._col] = 2;   //把走過的這個位置進行標記
	next = cur;
	if(next._row == n-1) //找到了一條路
	{
		if(shortpath.empty() || path.size()<shortpath.size())
		{
			shortpath = path;
		}
		path.pop();   //下面加了return,所以要先進行pop一次，不然出來的結果就會多一個點（讀者可自行驗證下）
		return ;   
	}
	//開始對上下左右進行探測
	//對上的探測
	next = cur;
	next._row -= 1;
	//檢查路是否可以通
	if(CheckIsAccess(maze,n,cur,next))
	{
		maze[next._row*n+next._col] = maze[cur._row*n+cur._col]+1;
		GetMazePath_r(maze,n,next,path,shortpath);
	}
	//對下的探測
	next = cur;
	next._row += 1;
	//檢查路是否可以通
	if(CheckIsAccess(maze,n,cur,next))
	{
		maze[next._row*n+next._col] = maze[cur._row*n+cur._col]+1;
		GetMazePath_r(maze,n,next,path,shortpath);
	}
	//對左的探測
	next = cur;
	next._col -= 1;
	//檢查路是否可以通
	if(CheckIsAccess(maze,n,cur,next))
	{
		maze[next._row*n+next._col] = maze[cur._row*n+cur._col]+1;
		GetMazePath_r(maze,n,next,path,shortpath);
	}
	//對右的探測
	next = cur;
	next._col += 1;
	//檢查路是否可以通
	if(CheckIsAccess(maze,n,cur,next))
	{
		maze[next._row*n+next._col] = maze[cur._row*n+cur._col]+1;
		GetMazePath_r(maze,n,next,path,shortpath);
	}
	//到這個位置，說明四個方向都走不通，進行回溯
	path.pop();  
}   


//列印迷宮
void Print(int* maze, size_t n)
{
	for(size_t i = 0; i<n; i++)
	{
		for(size_t j = 0; j<n; j++)
		{
			cout<<maze[i*n+j];
		}
		cout<<endl;
	}
}
int main()
{
	int maze[N][N];
	stack<Pos> path;
	Pos entry = {2,1};
	stack<Pos> shortpath;
	//輸出迷宮
	GetMaze((int*)maze,N);
	GetMazePath_r((int*) maze,N,entry,path,shortpath);
	Print((int*) maze,N);
    cout<<"是否找到迷宮："<<!path.empty()<<endl;
	return 0;
}
 

說了這麼多，機智的你應該掌握了吧。