給定$K$個整陣列成的序列{ N_1N​1​​, N_2N​2​​, ..., N_KN​K​​ }，“連續子列”被定義為{ N_iN​i​​, N_{i+1}N​i+1​​, ..., N_jN​j​​ }，其中 1 \le i \le j \le K$1\le i\le j\le K$。

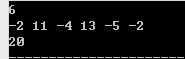
$“最大子列和”則被定義為所有連續子列元素的和中最大者。例如給定序列\{\; -2,\; 11,\; -4,\; 13,\; -5,\; -2\; \}，其連續子列\{\; 11,\; -4,\; 13\; \}有$

$最$大的和20。現要求你編寫程式，計算給定整數序列的最大子列和。

  可以線上性時間內求解！採用線上處理的方式，即每輸入一個數立即進行處理。該演算法的核心基於下面的事實：如果整數序列{a1, a2, ... , an}的最大和子列是{ai,ai+1,...,aj},那麼必有當前序列和ThisSum>=0(ThisSum = ai+ai+1+...al;   i <= l <= j};所以，一旦發現當前子列和為負，則可以重新開始考察一個新的子序列。

  詳細解法如下：

#include<stdio.h>
#include<stdlib.h>


int main()
{
int i, n, k, ThisSum = 0, MaxSum = 0;
scanf("%d", &n);
for(i=0; i<n; i++)
{
scanf("%d", &k);
ThisSum += k;
if(ThisSum > MaxSum)
{
MaxSum = ThisSum;
}
else if(ThisSum < 0)
  ThisSum = 0;
}

printf("%d", MaxSum);

return 0;

}