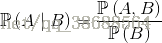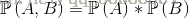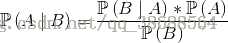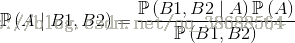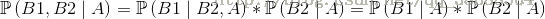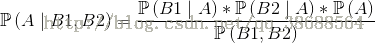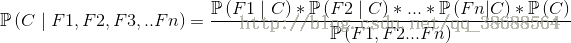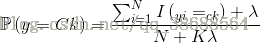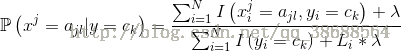1. 概率論相關數學公式
   條件概率:
   相互獨立事件：
   貝葉斯定理:
2. 樸素貝葉斯分類器
   眾所周知，樸素貝葉斯是一種簡單但是非常強大的線性分類器。它在垃圾郵件分類，疾病診斷中都取得了很大的成功。它只所以稱為樸素，是因為它假設特徵之間是相互獨立的，但是在現實生活中，這種假設基本上是不成立的。那麼即使是在假設不成立的條件下，它依然表現的很好，尤其是在小規模樣本的情況下。但是，如果每個特徵之間有很強的關聯性和非線性的分類問題會導致樸素貝葉斯模型有很差的分類效果。
   樸素貝葉斯指的兩方面：
   –|樸素：各個特徵之間相互獨立
   –|貝葉斯：基於貝葉斯定理
   證明過程
   1.設事件A1,B1,B2,在B1、B2同時發生的前提下，A發生的概率為
   
   2.設B1，B2相互獨立，則上式可以變換：
   3.於是得到如下公式：
   
   4.推廣：
   假設有F1,F2,F3,..Fn個特徵，即n維特徵
   有C1,C2,C3,…Cm個類別，m維類別，得到模型如下：
   
   C可以分別取每個類別，C1，C2等等，P(F1 | C1)即代表在C1所屬類別下F1特徵出現的條件概率。最後求出每個類別出現的概率，取最大值即是預測值最有可能出現的類別。
   由於分母項是常數，對每一項都相同，因此在求值的過程中我們常將其忽略。

3. 舉個例子
   根據症狀和職業來判定其最可能得什麼病。
   
   現在有一個人，是一個打噴嚏的建築工人，請問患上感冒的概率有多大？
   P(感冒|打噴嚏，建築工人)=P(打噴嚏|感冒)P(建築工人|感冒)*P(感冒)/P(打噴嚏，建築工人)=2/3

   1/3 * 3/6 /(3/6 * 2/6)=0.667
   同理可以求得患其他病的原因，求其最大值即可得到最可能患的病，其中分母是可以不用求得，這裡我也求了一下。
   注意： 在我們求條件概率時可能會出現 某一特徵出現可能性為0的情況，這樣概率就是0了，因此我們需要做平滑處理。
   –|拉普拉斯平滑
   在求先驗概率：
   其中K為類別的個數，lambda為運算元，當lambda取1時即為拉普拉斯平滑，當取值在[0,1]時為Lidstone平滑。
   求後驗概率（即條件概率）:
   設M維特徵的第j維有L個取值，則某維特徵的某個取值ajl，在給定某分類ck下的條件概率為：
   
   其中Li為第i維特徵最大取值

4. 程式碼實現：

這裡附上GitHub網址可以下載：
https://github.com/hangdj/native_bayes/blob/master/native_bayes_1.py
# coding:utf-8
import numpy
def loadDataSet():  # 構建一個簡單的文字集，以及標籤資訊 1 表示侮辱性文件，0表示正常文件
        postingList = [['my', 'dog', 'has', 'flea', 'problem', 'help', 'please'],
                       ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
                       ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
                       ['stop', 'posting', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
                       ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
                       ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
        classVec = [0, 1, 0, 1, 0, 1]
        return postingList, classVec

def createVocabList(dataSet):  # 統計詞彙，建立詞典
        vocabSet = set([])
        for document in dataSet:
            vocabSet = vocabSet | set(document)
        #print (vocabSet)
        return list(vocabSet)

def setOfWord2Vec(vocabList, inputSet):  # 建立詞頻統計向量,此方法為詞集模型，出現賦值1，or0
        returnVec = [] # 返回的文字向量與詞典大小保持一致
        for article in inputSet:
            tmp = [0] * len(vocabList)
            for word in article:
                if word in vocabList:
                    tmp[vocabList.index(word)] = 1  # 當前文件有這個詞條，則根據詞典位置獲取其位置並賦值為1
                else:
                    print ("the word :%s is not in my vocabulary" % word)
            returnVec.append(tmp)
        print(returnVec)
        return returnVec

def bagOfWord2Vec(vocabList, inputSet):  # 詞袋模型，統計概率的
        returnVec = []
        for article in inputSet:
            tmp=[0]*len(vocabList)
            for word in article:
                if word in vocabList:
                    tmp[vocabList.index(word)] += 1  # 當前文件有這個詞條，則根據詞典位置獲取其位置並賦值為1
                else:
                    print ("the word :%s is not in my vocabulary" % word)
            returnVec.append(tmp)
        print (returnVec)
        return returnVec
def trianNB(trainMatrix,trainCategory):#訓練生成樸素貝葉斯模型
    '''
    :param trainMatrix: 訓練陣列
    :param trainCategory: 訓練標籤
    :return:
    '''
    numTrainDoc=len(trainMatrix)#總共文件數量
    numWords=len(trainMatrix[0])#單詞數量
    pAbusive=sum(trainCategory)/numTrainDoc#統計侮辱性文件總個數，然後除以總文件個數
    p0Num=numpy.ones(numWords)
    p1Num=numpy.ones(numWords)
    p0Denom=2.0
    p1Denom=2.0
    for i in range(numTrainDoc):
        if trainCategory[i]==1:#如果是侮辱性文件
            p1Num+=trainMatrix[i]#把屬於同一類的文字向量相加，實質是統計某個詞條在該文字類中出現的頻率
            p1Denom+=sum(trainMatrix[i])#去重
            print(p1Denom,"p1Denom")
        else:
            p0Num+=trainMatrix[i]
            p0Denom+=sum(trainMatrix[i])
            print(p0Denom,"p0Denom")
    p1Vec=numpy.log(p1Num/p1Denom)#統計詞典中所有詞條在侮辱性文件中出現的概率
    p0Vec=numpy.log(p0Num/p0Denom)#統計詞典中所有詞條在正常性文件中出現的概率
    return pAbusive,p1Vec,p0Vec
def classifyNB(vec2classify,p0Vec,p1Vec,pClass1):# 引數1是測試文件向量，引數2和引數3是詞條在各個
                                                    #類別中出現的概率，引數4是P（C1）
    p1=numpy.sum(vec2classify*p1Vec)+numpy.log(pClass1)
    p0=numpy.sum(vec2classify*p0Vec)+numpy.log(1.0-pClass1)
    if p1>p0:
        return 1
    else:
        return 0
if __name__=='__main__':
    test=[['mr', 'licks', 'ate', 'my', 'steak', 'how', 'food', 's']]
    #test=[['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid']]
    postingList, classVec=loadDataSet()#文件，標籤
    vocabList=createVocabList(postingList)#詞典
    returnVec=bagOfWord2Vec(vocabList,postingList)#文字向量
    pAbusive, p1Vec, p0Vec=trianNB(returnVec,classVec)#侮辱性文件比例，侮辱文件概率，正常文件概率
    print (pAbusive, p1Vec, p0Vec)
    testVec=bagOfWord2Vec(vocabList,test)
    pclass=classifyNB(testVec,p0Vec,p1Vec,pAbusive)
    print (pclass)
'''
{1: {0: {1: 0.25, 2: 0.3333333333333333, 3: 0.4166666666666667}, 1: {4: 0.16666666666666666, 5: 0.4166666666666667, 6: 0.4166666666666667}},
 -1: {0: {1: 0.4444444444444444, 2: 0.3333333333333333, 3: 0.2222222222222222}, 1: {4: 0.4444444444444444, 5: 0.3333333333333333, 6: 0.2222222222222222}}} conditional_prob
'''

5.樸素貝葉斯三種模型
多項式模型：特徵：單詞，值：k類單詞出現頻次
在多項分佈樸素貝葉斯模型中，特徵向量 X 的特徵 通常為 離散型變數，並且假定所有特徵的取值是符合多項分佈的，可用於文字分類。
在多項式模型中， 設某文件d=(t1,t2,…,tk)，tk是該文件中出現過的單詞，允許重複，則
**先驗概率**P(c)= 類c下單詞總數/整個訓練樣本的單詞總數
**類條件概率**P(tk|c)=(類c下單詞tk在各個文件中出現過的次數之和+1)/(類c下單詞總數+|V|)
V是訓練樣本的單詞表（即抽取單詞，單詞出現多次，只算一個），|V|則表示訓練樣本包含多少種單詞。
P(tk|c)可以看作是單詞tk在證明d屬於類c上提供了多大的證據，而P(c)則可以認為是類別c在整體上佔多大比例(有多大可能性)。
舉例：

# coding:utf-8
import numpy as np
#以單詞為計量單位
class MultinomialNB(object):
    '''
    :parameter
        alpha :平滑引數
            -->0 不平滑
            -->0-1 Lidstone 平滑
            -->1 Laplace 平滑
        fit_prior:boolean
            是否學習類先驗概率。
      如果fasle，則會使用統一的優先順序。
        class_prior:array-like, size (n_classes,) 陣列格式 大小 類別個數
            這些類的先驗概率，如果指定的話，先驗概率將不會根據資料計算
    Attributes
    fit(X,y):特徵和標籤 都是陣列
    predict(X:
    '''
    def __init__(self,alpha=1.0,fit_prior=True,class_prior=None):
        self.alpha=alpha
        self.fit_prior=fit_prior
        self.class_prior=class_prior
        self.classes=None
        self.conditional_prob=None
    def _calculate_feature_prob(self,feature):#計算條件概率
        values=np.unique(feature)
        #print(values,'sddd')
        total_num=float(len(feature))
        value_prob={}
        for v in values:#有平滑效果
            value_prob[v]=((np.sum(np.equal(feature,v))+self.alpha)/(total_num+len(values)*self.alpha))
        return value_prob
    def fit(self,X,y):
        self.classes=np.unique(y)
        #計算先驗概率
        if self.class_prior==None:#不指定先驗概率
            class_num=len(self.classes)#類別個數
            if not self.fit_prior:#是否自學先驗概率，false則統一指定
                self.class_prior=[1.0/class_num for _ in range(class_num)]#統一優先順序
            else:
                self.class_prior=[]
                sample_num=float(len(y))
                for c in self.classes:
                    c_num=np.sum(np.equal(y,c))
                    self.class_prior.append((c_num+self.alpha)/(sample_num+class_num*self.alpha))#根據標籤出現個數計算優先順序
                #print(self.class_prior,"class_prior")
        #計算條件概率
        self.conditional_prob={}#like { c0:{ x0:{ value0:0.2, value1:0.8 }, x1:{}, c1:{...} }
        for c in self.classes:
            self.conditional_prob[c]={}
            #print(len(X[0]),"X[0]")
            for i in range(len(X[0])):#特徵總數2
                #print(X[np.equal(y,c)][:,1],"y==c")
                feature=X[np.equal(y,c)][:,i]#這裡加個逗號才是遍歷所有行！！！
                #print(feature,i,"feature")
                self.conditional_prob[c][i]=self._calculate_feature_prob(feature)
        print(self.conditional_prob,"conditional_prob")
        return self

    #給了 單詞概率{value0:0.2,value1:0.1,value3:0.3,.. } 和目標值 給出目標值的概率
    def _get_xj_prob(self, values_prob,target_value):
         return values_prob.get(target_value)
    #依據(class_prior,conditional_prob)預測一個簡單地樣本
    def _predict_single_sample(self,x):
        label=-1
        max_posterior_prob=0
        #對每一個類別，計算其後驗概率：class_prior*conditional_prob
        for c_index in range(len(self.classes)):
            current_class_prior=self.class_prior[c_index]#類別優先順序，類別多的優先順序大
            current_conditional_prob=1.0#條件概率
            feature_prob=self.conditional_prob[self.classes[c_index]]#類別1的條件概率
            #print(feature_prob.keys(),"feature_prob")
            j=0
            for feature_i in feature_prob.keys():#每一個特徵下的概率
                current_conditional_prob*=self._get_xj_prob(feature_prob[feature_i],x[j])
                j+=1

            #比較後驗概率，更新max_posterior_prob ,label
            print( current_class_prior*current_conditional_prob,self.classes[c_index],"後驗概率")
            if current_class_prior*current_conditional_prob>max_posterior_prob:#取最大的後驗概率
                max_posterior_prob=current_class_prior*current_conditional_prob
                label=self.classes[c_index]

        return label
    def predict(self,X):
        if X.ndim==1:
            return self._predict_single_sample(X)
        else:
            labels=[]
            for i in range(X.shape(0)):
                label=self._predict_single_sample(X[i])
                labels.append(label)
            return labels
if __name__=='__main__':
    X = np.array([
                          [1,1,1,1,1,2,2,2,2,2,3,3,3,3,3],
                          [4,5,5,4,4,4,5,5,6,6,6,5,5,6,6]
                 ])
    X = X.T
    y = np.array(        [-1,-1,1,1,-1,-1,-1,1,1,1,1,1,1,1,-1])
    nb = MultinomialNB(alpha=1.0,fit_prior=True)
    nb.fit(X,y)
    print ("[2,5]-->",nb.predict(np.array([2,5])))#輸出1 0.08169 0.04575
    print ("[2,4]-->",nb.predict(np.array([2,4])))#輸出-1 0.0327 0.0610

伯努利模型：特徵：文字，值：k類文字出現頻次
在伯努利樸素貝葉斯模型中，每個特徵的取值是布林型，或以0和1表示，所以伯努利模型中，每個特徵值為0或者1。
計算方式：
* P(c) *= 類c下檔案總數/整個訓練樣本的檔案總數
P(tk|c)=(類c下包含單詞tk的檔案數+1)/(類c的文件總數+2)
上面兩個模型區別：
–|二者的計算粒度不一樣，多項式模型以單詞為粒度，伯努利模型以檔案為粒度，因此二者的先驗概率和類條件概率的計算方法都不同。
–|計算後驗概率時，對於一個文件d，多項式模型中，只有在d中出現過的單詞，才會參與後驗概率計算，伯努利模型中，沒有在d中出現，但是在全域性單詞表中出現的單詞，也會參與計算，不過是作為“反方”參與的。
高斯模型：特點：只有它適用於連續變數預測（如身高預測）
在高斯樸素貝葉斯模型中，特徵向量 X 的特徵 通常為 連續型變數，並且假定所有特徵的取值是符合高斯分佈的，即：

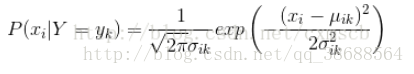
需要求每一維特徵的均值和方差。
舉例：

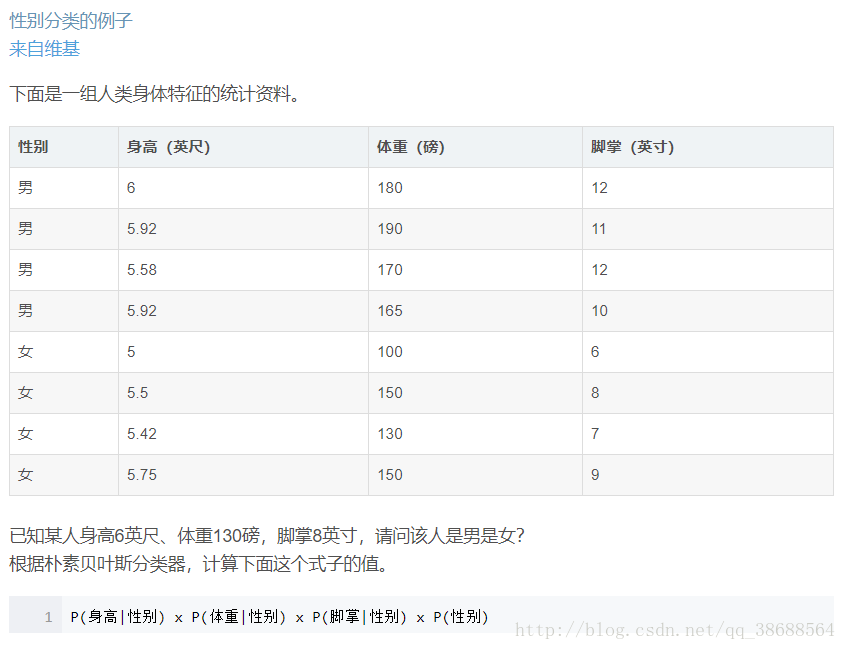
這裡的困難在於，由於身高、體重、腳掌都是連續變數，不能採用離散變數的方法計算概率。而且由於樣本太少，所以也無法分成區間計算。怎麼辦？
這時，可以假設男性和女性的身高、體重、腳掌都是正態分佈，通過樣本計算出均值和方差，也就是得到正態分佈的密度函式。有了密度函式，就可以把值代入，算出某一點的密度函式的值。
比如，男性的身高是均值5.855、方差0.035的正態分佈。所以，男性的身高為6英尺的概率的相對值等於1.5789（大於1並沒有關係，因為這裡是密度函式的值，只用來反映各個值的相對可能性）。

 P(身高=6|男) x P(體重=130|男) x P(腳掌=8|男) x P(男) 
　　　　= 6.1984 x e-9
　　P(身高=6|女) x P(體重=130|女) x P(腳掌=8|女) x P(女) 
　　　　= 5.3778 x e-4

# coding:utf-8
#當特徵是連續變數的時候，運用多項式模型就會導致很多P(xi|yk)==0（不做平滑的情況下），
# 此時即使做平滑，所得到的條件概率也難以描述真實情況。所以處理連續的特徵變數，應該採用高斯模型。

#高斯模型假設每一維特徵都服從高斯分佈,需要計算每一維的均值和方差
from self_multinomalNB import MultinomialNB
import numpy as np
#繼承Multinomial並重載相應的方法
class GaussianNB(MultinomialNB):
    def _calculate_feature_prob(self,feature):#計算平均值和方差
        mu=np.mean(feature)
        sigma=np.std(feature)
        return (mu,sigma)
    #計算高斯分佈的概率密度
    def _prob_gaussian(self,mu,sigma,x):
        return (1.0/(sigma*np.sqrt(2*np.pi)))*np.exp(-(x-mu)**2/(2*sigma**2))
    def _get_xj_prob(self, mu_sigma,target_value):
        return self._prob_gaussian(mu_sigma[0],mu_sigma[1],target_value)
if __name__=='__main__':
    X = np.array([
                          [1,1,1,1,1,2,2,2,2,2,3,3,3,3,3],
                          [4,5,5,4,4,4,5,5,6,6,6,5,5,6,6]
                 ])
    X = X.T
    y = np.array(        [-1,-1,1,1,-1,-1,-1,1,1,1,1,1,1,1,-1])
    nb = GaussianNB(alpha=1.0,fit_prior=True)
    nb.fit(X,y)
    print ("[2,5]-->",nb.predict(np.array([2,5])))#輸出1 0.08169 0.04575
    print ("[2,4]-->",nb.predict(np.array([2,4])))#輸出-1 0.0327 0.0610

6.參考文獻

我的GitHub上有全部程式碼，自己實現的包括呼叫API的：大家可以下載分享：
https://github.com/hangdj/native_bayes
部落格：http://blog.csdn.net/u012162613/article/details/48323777
http://blog.csdn.net/zhihaoma/article/details/51052064
ps（我的多項式模型沒有實現，這個待完善）