Fortran產生正態分佈的隨機數
Fortran中用來產生隨機數的函式是RANDOM_NUMBER(不需要再呼叫子程式RANDOM_SEED)。在fcode網站上已經對fortran產生隨機數(http://fcode.cn/guide-96-1.html)和fortran產生正態分佈的函式(http://fcode.cn/code_prof-33-1.html)進行了介紹。但是隨著gfortran版本的升級,生成隨機數的語句需要適當的改變。
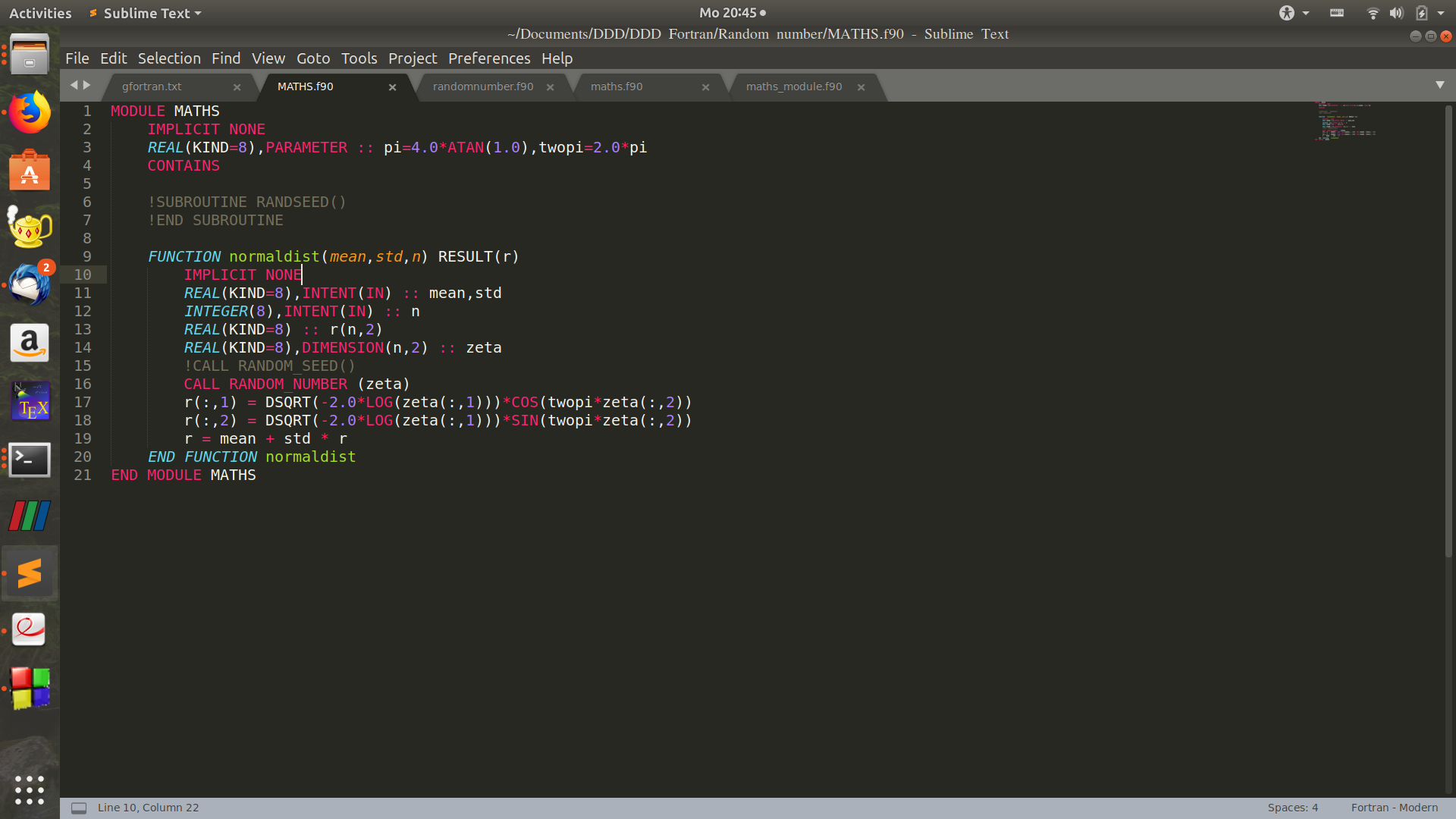
上圖中的MATHS模組可以用來產生正態分佈的隨機數。mean是均值,std是標準差,r表示需要產生的正態分佈隨機數的個數(n*2的陣列)。gfortran 7.2 版本之後,不再需要呼叫RANDOM_SEED子程式(每次執行產生的隨機數是變化的——本人親測)。對於intel fortran編譯器本人也進行了測試去掉CALL RANDOM_SEED()語句之後,程式產生的正態分佈隨機數永遠一樣。對於可能用IVF和gfortran的讀者來說,最好加上語句CALL RANDOM_SEED()語句。
本文對gfortran 7.2 及其以上版本的產生正態分佈的隨機數進行了簡單的說明。
如果讀者在用本文的程式或方法時最好先對其進行測試,以排除不同機器或編譯器的影響。
希望和大家共同交流進步。
相關推薦
Fortran產生正態分佈的隨機數
Fortran中用來產生隨機數的函式是RANDOM_NUMBER(不需要再呼叫子程式RANDOM_SEED)。在fcode網站上已經對fortran產生隨機數(http://fcode.cn/guide-96-1.html)和fortran產生正態分佈的函式(http://
Matlab中產生正態分佈隨機數的函式normrnd-----用來產生高斯隨機矩陣
>> help normrnd NORMRND Random arrays from the normal distribution. R = NORMRND(MU,SIGMA) returns an array of random numbers chosen from a normal
【matlab】Matlab中產生正態分佈隨機數的函式normrnd
Date: 2018.8.5 功能:生成服從正態分佈的隨機數 語法: R=normrnd(MU,SIGMA) R=normrnd(MU,SIGMA,m) R=normrnd(MU,SIGMA,m,n) 說 明: R=normrnd(MU
JAVA自定義演算法產生正態分佈隨機數
一、為什麼需要服從正態分佈的隨機函式 一般我們經常使用的隨機數函式 Math.random() 產生的是服從均勻分佈的隨機數,能夠模擬等概率出現的情況,例如 扔一個骰子,1到6點的概率應該相等,但現實生活中更多的隨機現象是符合正態分佈的,例如20歲成年人的體重分佈等。 假如我們在製作一個遊戲,要
C產生正態分佈隨機數寫入檔案並讀出後用快速排序法排序
基於快速排序法的正態隨機數排序 使用中心極限定理產生正態分佈隨機數 使用快速排序法進行排序 讀寫資料到記事本 程式計時 #include <stdio.h> #include <stdlib.h> #include <mat
正態分佈隨機數的產生
最近平凡聽到關於正態分佈取樣相關的內容,突然想到一個問題: 到底如何利用正態分佈取樣? 正好近期模式識別課程上也有一個相關的內容,整理了一下查到的資料。 一。柱狀圖估計分佈 假設樣本 x N(u,θ) x~N(u, \theta), 其pdf圖如下:
C#產生正態分佈、泊松分佈、指數分佈、負指數分佈隨機數(原創)
http://blog.sina.com.cn/s/blog_76c31b8e0100qskf.html 在程式設計過程中,由於資料模擬模擬的需要,我們經常需要產生一些隨機數,在C#中,產生一般隨機數用Random即可,但是,若要產生服從特定分佈的隨機數,就需要一定的演
產生服從正態分佈隨機數(轉載)
一、為什麼需要服從正態分佈的隨機函式 一般我們經常使用的隨機數函式 Math.random() 產生的是服從均勻分佈的隨機數,能夠模擬等概率出現的情況,例如 扔一個骰子,1到6點的概率應該相等,但現實生活中更多的隨機現象是符合正態分佈的,例如20歲成年人的體重分佈等。
java隨機數產生- 正態分佈
正態分佈 java.util.Random裡的nextGaussian(),生成的數值符合均值為0方差為1的高斯/正態分佈,即符合標準正態分佈。 產生數字的範圍:任何數都有可能,不過在0左右的數字較多。 產生N(a,b)的數:Math.sqrt(b)*random.next
randn:產生正態分佈的隨機數或矩陣的函式
randn:產生均值為0,方差σ^2 = 1,標準差σ = 1的正態分佈的隨機數或矩陣的函式。用法:Y = randn(n):返回一個n*n的隨機項的矩陣。如果n不是個數量,將返回錯誤資訊。Y = randn(m,n) 或 Y = randn([m n]):返回一個m*n的隨
np.random.rand均勻分佈隨機數和np.random.randn正態分佈隨機數函式使用方法
np.random.rand用法 覺得有用的話,歡迎一起討論相互學習~Follow Me 生成特定形狀下[0,1)下的均勻分佈隨機數 np.random.rand(a1,a2,a3…)生成形狀為(a1,a2,a3…),[0,1)之間的 均勻分佈 隨機數 np
MATLAB實現由均勻分佈產生正態分佈和銳利分佈
xaxis=-10:0.1:10; miu=0; delta=1; N=1000000; u1=rand(1,N); u2=rand(1,N); y1=(-2*log(u1)).^0.5; y2=
正態分佈隨機數生成演算法
最近在學習基於蒙特卡羅的強化學習方法時遇到 生成服從正態分佈的隨機數的演算法,因此做一個回顧和總結。要程式設計得到服從均勻分佈的偽隨機數是容易的,C、Python、Java語言等都提供了相應的函式。但是要想生成服從正態分佈的隨機數就沒那麼容易了,生成服從正態分佈的隨機數的基本
利用均勻分佈和中心極限定理產生正態分佈(高斯分佈)
中心極限定理: 設隨機變數序列{Xi}相互獨立,具有相同的期望和方差,即E(Xi)=μ,D(Xi)=σ2,令Yn=X1+...+Xn,Zn=Yn−E(Yn)D(Yn)√=Yn−nμn√σ,則Zn→N(
如何用均勻分佈隨機數生成正態分佈隨機數
前言 在Monte Carlo模擬技術中,許多地方都需要用到符合標準正態分佈(高斯)的隨機數來設計取樣方案,因此瞭解如何用均勻分佈隨機數(實際上是均勻分佈的偽隨機數)來生成標準正態分佈的隨機數十分重要。本文將對這個最基本的問題做討論,並提供c++11程式
正態分佈隨機數生成器
import math,random u=1800. q=800. reslist=[] for v in xrange(0,3600): y=math.exp(-((v-u)/q)*((v-u)/q)/2)/(q*math.sqrt(2*3.14159265359)
概率演算法-均勻分佈產生正態分佈
大部分語言只能產生均勻分佈的隨機數。C語言用(double)rand()/RAND_MAX產生0到1之間均勻分佈的隨機數。那麼如何產生正態分佈的呢? 一般,一種概率分佈,如果其分佈函式為y=F(x),那麼,y的範圍是0~1,求其反函式G,然後產生0到1之間的隨
課堂練習--計算陣列的最大值,最小值,平均值,標準差,中位數;numpy.random模組提供了產生各種分佈隨機數的陣列;正態分佈;Matplotlib
#計算陣列的最大值,最小值,平均值,標準差,中位數 import numpy as np a=np.array([1, 4, 2, 5, 3, 7, 9, 0]) print(a) a1=np.max(a) #最大值 print(a1) a2=np.min(a) #最小值 print(a2) a3
使用rand()產生服從高斯/正態分佈的隨機數
我們藉助於rand()去生成高斯/正態分佈。 當然,rand是偽隨機的問題在此先不考慮。 (1)用Box-Muller方法,隨機抽出兩個從均勻分佈的數字和。然後 那和都是正態分佈的。 證明可用極座標,請參考教科書中的Box-Muller方法。 C程式碼: #
如何用JAVA產生符合正態分佈的隨機數
正態分佈 java.util.Random裡的nextGaussian(),生成的數值符合均值為0方差為1的高斯/正態分佈,即符合標準正態分佈。 產生數字的範圍:任何數都有可能,不過在0左右的數字較多。 產生N(a,b)的數:Math.sqrt(b)*random.nextGaussian()+a; 即