使用動態規劃法解決0/1揹包問題
問題:
給定n種物品和一個揹包i(1<=i<=n)的重量是Wi,其價值為Vi,揹包的容量為C,對每種物品只能有兩種選擇:裝入或者不裝入揹包。如何選擇裝入揹包的物品使得裝入揹包中的物品的總價值最大?
演算法使用C++語言實現:
/**w[]:物品的重量陣列:2,2,6,5,4
v[]:物品的價值陣列:6,3,5,4,6
n:物品的數量:5
C:揹包的容量:10
x[5]:儲存物品拿與不拿的狀態的陣列
*/
#include<iostream.h>
int max(int a,int b)
{
if(a>=b)
return a;
else return b;
}
int KnapSack(int n,int w[],int v[],int x[],int C)
{
int i,j;
for(i=0;i<=n;i++)
V[i][0]=0;
for(j=0;j<=C;j++)
V[0][j]=0;
for(i=0;i<=n-1;i++)
for(j=0;j<=C;j++)
if(j<w[i])
V[i][j]=V[i-1][j];
else
V[i][j]=max(V[i-1][j],V[i-1][j-w[i]]+v[i]);
j=C;
for(i=n-1;i>=0;i--)
{
if(V[i][j]>V[i-1][j])
{
x[i]=1;
j=j-w[i];
}
else
x[i]=0;
}
cout<<"選中的物品是:"<<endl;
for(i=0;i<n;i++)
cout<<x[i]<<endl;
return V[n-1][C];
}
void main()
{
int s;//獲得的最大價值
int w[5];//物品的重量
int v[5];//物品的價值
int x[5];//物品的選取狀態
int n,i;
int C;//揹包最大容量
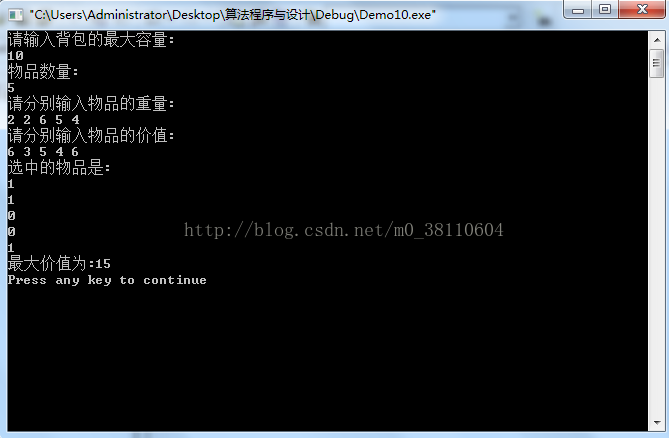
cout<<"請輸入揹包的最大容量:"<<endl;
cin>>C;
cout<<"物品數量:"<<endl;
cin>>n;
cout<<"請分別輸入物品的重量:"<<endl;
for(i=0;i<n;i++)
cin>>w[i];
cout<<"請分別輸入物品的價值:"<<endl;
for(i=0;i<n;i++)
cin>>v[i];
s=KnapSack(n,w,v,x,C);
cout<<"最大價值為:"<<s<<endl;
}
相關推薦
使用動態規劃法解決0/1揹包問題
問題: 給定n種物品和一個揹包i(1<=i<=n)的重量是Wi,其價值為Vi,揹包的容量為C,對每種物品只能有兩種選擇:裝入或者不裝入揹包。如何選擇裝入揹包的物品使得裝入揹包中的物品的總價
動態規劃法解決0/1揹包問題詳解
是什麼 動態規劃(dynamic programming)是求解決策過程最優化的數學方法,把多階段過程轉換為一系列單階段問題,利用各階段之間的關係,逐個求解,創立了解決這類過程優化問
【演算法】動態規劃解決0-1揹包的兩個疑惑
1. 揹包問題 描述: 給定 n 種物品,每種物品有對應的重量weight和價值value,一個容量為 maxWeight 的揹包,問:應該如何選擇裝入揹包的物品,使得裝入揹包中的物品的總價值最大? 過程: a) 把揹包問題抽象化(X1,X2,…,Xn,其中 Xi
動態規劃法例子 0-1揹包問題
/* 動態規劃法例子 0-1揹包問題 */ //物品個數 const int n = 5; // 重量 int Weight[n] = {3,4,7,8,9}; // 價值 int Values[n] = {4,5,10,11,13}; // 揹包總
分支界限法解決0/1揹包問題
1.堆 1 #include<iostream> 2 #include<algorithm> 3 using namespace std; 4 #define N 100 //最多可能物體數 5 struct goods //物品結構體 6
動態規劃之0-1揹包問題(POJ3624)
有N件物品和一個容積為M的揹包。第i件物品的體積w[i],價值是d[i]。求解將哪些物品裝入揹包可使價值總和最大。每種物品只有一件,可以選擇放或者不放。(N<=3500,M<=130000)。 解題思路: 用F[i][j]表示取前i種物品,使它們總體積不超過j的最優取法取
動態規劃實現0-1揹包問題
//動態規劃實現0-1揹包 public class DN01 { public static void dy(int []v,int []w,int c,int [][]m){ int n=v.length-1; //i=n int jMax=Math.min(w[n]-1,
動態規劃之0-1揹包問題
問題: 物品集合s={1,2,3,4,…,n},物品i的重量為wi,其價值為vi,揹包的容量(最大載重量)為W,如何裝使物品價值最大。(物品不能分割) 分析: p(i,j)是揹包容量為j,可選物品為i(i+1,…,n)時的最優解 (“將前i個物品放入容量為j的揹
動態規劃之0-1揹包問題,鋼條切割
動態規劃 首先說說動態規劃:動態規劃與分治法相似,都是組合子問題的解來解決原問題的解,與分治法的不同在於:分治法的子問題是相互獨立存在的,而動態規劃應用於子問題重疊的情況。 設計動態規劃演算法的步驟: 1、刻畫一個最優解的結構特徵 2、遞迴地定義最優解的
貪心演算法解決0-1揹包問題
揹包問題描述如下: 已知 揹包容量M=120 物品種類數n=10 各種物品的總效益pi(i=1,2,………10) : 50,60,70,80,90,80,70,60,50,40 各種物品的總重量wi(i=1,2………10) : 17,30,25,41,80,
動態規劃解0-1揹包問題(C語言版)
這學期開的演算法課,感覺好難,光這個問題就弄了好久,我這裡的程式碼非本人原創程式碼,都是借鑑網上的程式碼按自己的理解加以改進的,原網頁地址 為http://www.cnblogs.com/qinyg/archive/2012/04/26/2471829.html 問題描
回溯法解決0-1揹包問題
問題描述: 有n件物品和一個容量為c的揹包。第i件物品的價值是v[i],重量是w[i]。求解將哪些物品裝入揹包可使價值總和最大。所謂01揹包,表示每一個物品只有一個,要麼裝入,要麼不裝入。 回溯法: 01揹包屬於找最優解問題,用回溯法需要構造解的子
動態規劃解0-1揹包問題
題目如下: 試用動態規劃的方法,求解0-1揹包問題:有一揹包,能裝入物體總重量為C,有n個物體,重量為w1,w2,..,wn,價值分別為v1,v2,…vn。試求一種裝載方案,使得揹包裝載的物體總價值最大。其中,C, w都是整數。 解題思路: 簡單dp 試用動態規劃
動態規劃問題——0/1揹包問題(Java實現)
1、問題描述0-1揹包問題: 給定N件物品和一個容量為V的揹包。放入第i件物品耗費的空間為C[i] ,得到的價值是 W[i] 。 問:哪些物品裝入揹包可使價值總和最大?最大是多少?2、基本思路2.1 基本思路 這是最基礎的揹包問題,特點是:每
用模擬退火演算法解決0-1揹包問題
clear clc a = 0.95 k = [5;10;13;4;3;11;13;10;8;16;7;4]; k = -k; % 模擬退火演算法是求解最小值,故取負數 d = [2;5;18;3;2;5;10;4;11;7;14;6]; restriction = 46;
動態規劃演算法0-1揹包問題java實現
問題描述:給定n種物品和一揹包,物品i的重量是wi,其價值是pi,揹包的容量是M,問如何選擇裝入揹包中的物品總價值最大? import java.util.ArrayList; import java.util.HashMap; /* * 實際就是一種分而治之的思想
實驗2 動態規劃法求解最長公共子序列問題&0-1揹包問題
1 求最長公共子序列問題 1.1 概念 1.1.1 子序列 子序列: 一個序列A = a1,a2,…,an中任意刪除若干項,剩餘的序列叫做A的一個子序列。也可以認為是從序列A按原順序保留任意若干項得
0-1揹包問題,用滾動陣列,動態規劃解決
接觸了很多的0-1揹包的問題,這個問題是動態規劃的經典題,總結一下,加深自己的印象,也 為大家做個參考,對blog有問題可以直接評論,我會盡快的回答! 題目:有N件物品和一個容量為V的揹包,第i件物品的體積w[i],價值是c[i],求解將那些物品裝入揹包 可使這些物品的費
動態規劃法—0-1揹包問題(一)
0-1揹包問題 問題描述 給定n個物品和一揹包。物品i的重量是wi,其價值為vi,揹包的容量為W。應如何選擇裝入揹包的物品,使得裝入揹包中物品的總價值最大? 約束條件 放入揹包的物
0/1揹包問題(回溯法、分支限界法、動態規劃法、貪心法)(C++版)
此篇整理自李老師上課PPT --- On one way by myself(1)問題描述 有n個重量分別為{w1,w2,…,wn}的物品,它們的價值分別為{v1,v2,…,vn},給定一個容量為W的揹包。設計從這些物品中選取一部分物品放入該揹包的方