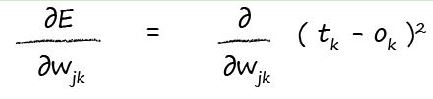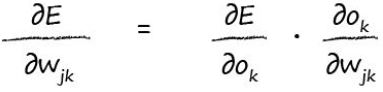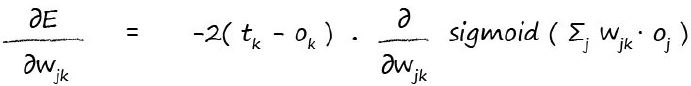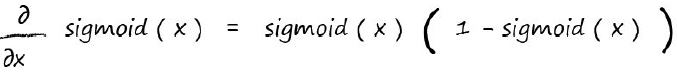Make Your Own Neural Network(十四)-----實際上是如何更新權重(二)
神經網路的輸出是一個包含非常多權重引數的複雜函式。我們能夠使用梯度下降法求得其權重嗎?只要我們能夠使用正確的誤差函式就可以求得出神經網路中權重的引數值。
神經網路的輸出本身並不是一個誤差函式。但是我們能夠輕鬆的將它轉換為誤差函式,因為誤差是訓練樣本目標值與神經網路輸出值之間的差值。
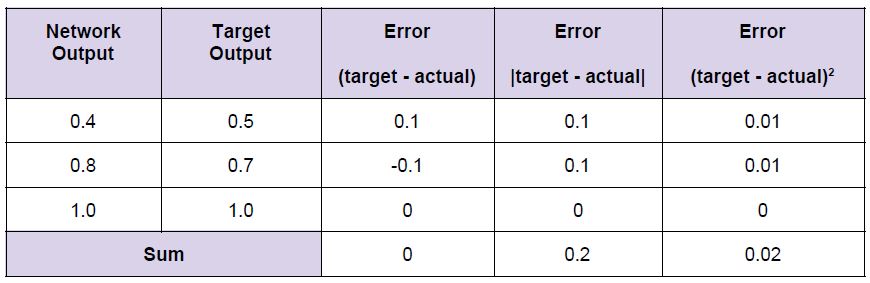
如下表所示。下表標註了三個輸出節點的訓練值和實際的輸出值,以及它們之間的誤差值。
第一個候選誤差函式非常簡單,即目標值-實際輸出值。這看起來很合理不是?如果我們以所有節點的誤差和這個角度來度量神經網路訓練的是否足夠好,你將觀察到其誤差和為0!!
怎麼回事?很明顯,神經網路並沒有被很好的訓練,因為兩個輸出節點的值與目標值不一樣,並且誤差和為0意味著沒有誤差!!由於正負誤差剛剛抵消了所以出現了誤差和為0。即使誤差沒有完全的抵消,我們也可以觀察到這是一種比較差的誤差測量法。
讓我們用實際輸出值和目標值之間的絕對值來測量誤差。這意味著我們將忽略符號,並即為|目標值-實際值|。最後誤差求和時並沒有完全的抵消。但是實際我們並不採用這種方法測量誤差,因為在梯度下降法中靠近最小值的時候,其斜率並不是連續的,導致梯度下降法並不能很好的發揮作用。
第三種誤差測量函式使用的是(目標值-實際值)的平方。我們採用這種函式測量誤差主要是基於如下幾點:
1.梯度下降法中求解斜率的時候比較容易。
2.這個誤差函式時平滑而連續的,能夠很好的發揮梯度下降法的優勢
3.當靠近最小值的時候,梯度值越來越小。這意味著我們將使用平滑的步長靠近最小值,從而避免越過最小值的風險。
下面小節中我們將採用第三種誤差測量函式。有人會問,有沒有第四種誤差測量函式呢?是的,當然有。你可以構建其他誤差測量函式。有些不能很好的適用,有些只是針對特定的問題適用。
好了!在開始計算自變數是權重的誤差函式之前,我們有些預備知識需要了解---微積分。你可能已經很熟悉微積分了,如果你不是很熟悉或者只是大概瞭解一些,本書的附錄將包含一些這方面的介紹。微積分在數學上描述的是當一個變數變化時,另外一個變數將做如何變化。比如說,彈簧的長度改變時,彈簧的彈力將如何改變。對於神經網路而言,我們關心的是誤差函式將隨著權重的改變做何種改變。
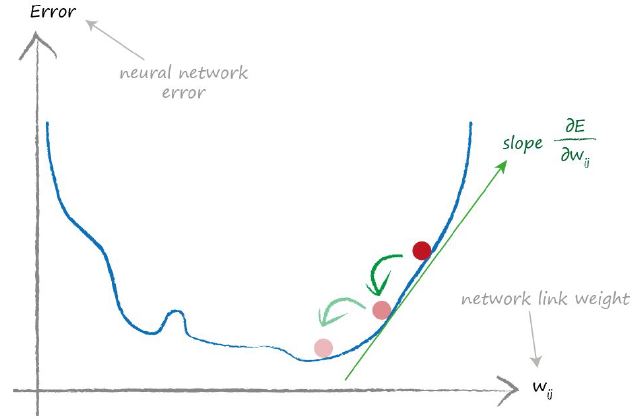
讓我們從一幅圖畫開始。
就像上一小節那樣,圖例中我們並沒有做過多的修改。但是這次我們想獲得的最小值指的是神經網路中誤差的最小值。我們需要修改的引數是神經網路中的斜率。在這簡單的例子中,我們只是標示了一個權重值,但是你要知道的是神經網路中將會有很多的權重值。
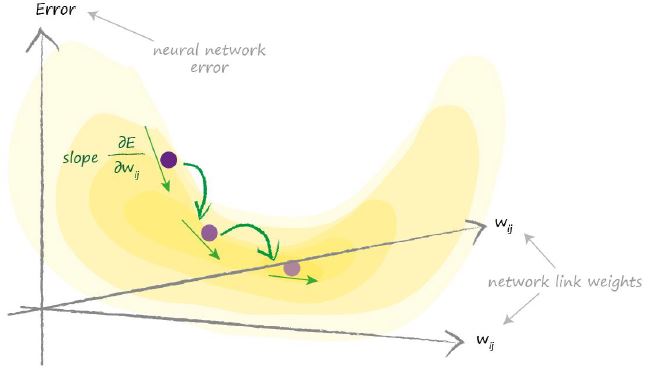
下圖表示的是兩個權重值,並且誤差函式中包含兩個權重引數。我們試圖求得最小誤差值的過程有點像之前複雜地形中找到最低山谷的過程。
對於有很多引數得誤差函式來說,我們很難直觀的用視覺化的方式呈現。但是我們在這個多維平面中找最小值所使用的梯度下降法和之前是一樣的。
讓我們用數學公式寫出下面的誤差函式的相關梯度結果: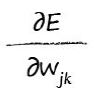
這個偏導數表示的是當權重Wjk變化時,誤差E將怎樣變化。這個偏導數表示的是誤差函式靠近最小值的斜率。
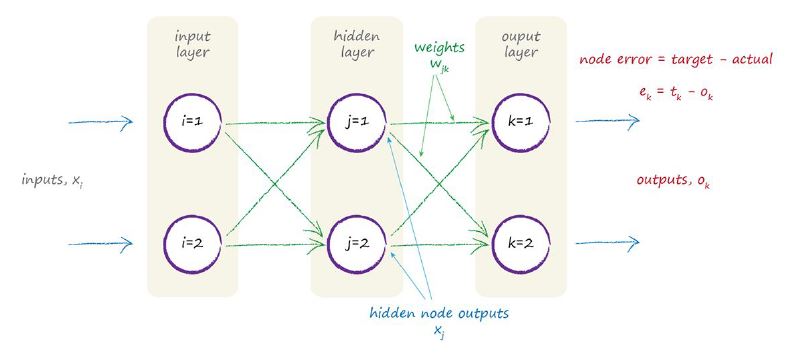
在我們詳細解釋這個表示式之前,讓我們專注於隱藏層和最後輸出層之間一個節點的情況。如下圖高亮度標註。我們將會回到這張圖,闡述輸出層與隱藏層之間權重的計算方法。
在後續計算微積分的時候,我們將會提到上面這幅圖,確保我們不會忘記每一個符號所代表的含義。別太緊張,後續計算步驟並不難並且會一一解釋。所有的概念在之前的小節中已經闡述過了。
首先,讓我們擴充套件下神經網路的誤差函式:神經網路輸出層n個輸出節點的目標值和實際值之間差值的平方和,即
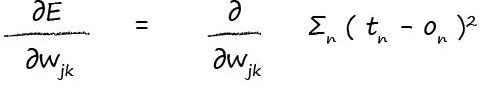
現在我們做的只是把實際的誤差函式寫出來。
我們可以簡化上述公式,第n個輸出節點的輸出結果為On,只取決於前向神經網路層與它相連的節點。這意味著對於節點K,其輸出結果Ok只取決於權重Wjk。因為只有這些節點與節點k相連。
從另外一個角度來看,節點k的輸出結果並不取決於權重wjb,b不等於k。因為節點k與前向節點b之間並無連線。權重Wjb表示的是與輸出節點b相連的權重而不是與輸出節點k相連的權重。
這意味著我們可以把上述公式中n個輸出結果中只與輸出節點k的輸出結果,因為ok只取決於Wjk。
至此,你可能意識到對於某一個節點來說,並不需要計算所有節點的誤差平方和。因為輸出節點的輸出誤差只取決於與之相連節點的權重值。
總之,我們有了一個更為簡單的表示式:
現在我們可以開始微積分計算了。
tk是一個常量,它不會隨著Wjk的變化而變化。即tk並不是Wjk的函式。公式中的Ok這部分取決於權重wjk。我們將用到微積分的鏈式規則把上述公式中分幾步進行微積分運算。即:
現在我們可以分別計算每一個部分。第一部分是對一個簡單的二次方函式求導。即:
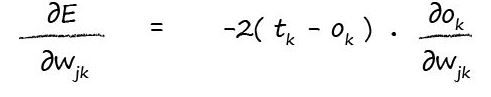
第二部分需要稍微思考下,但是也並不難。如果你還記得前面小節的話,節點k的輸出結果Ok是與前一層相連節點輸出結果加權和應用於sigmoid啟用函式之後的輸出結果。讓我們寫下如下公式:
其中Oj是隱藏層j節點的輸出結果,而不是最後一層的輸出結果Ok。
我們該如何對sigmoid函式求導呢?用鏈式法則和e的指數求導法則,可得到如下公式
有些函式求導之後,求導結果會非常複雜。但是sigmoid啟用函式卻是相對簡單的一個結果。這也是為什麼sigmoid函式在神經網路中大量使用的原因。
讓我們繼續計算最後的結果:
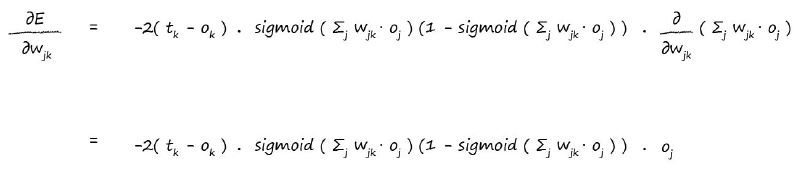
這是一個神奇的表示式。我們將使用這個表示式對神經網路進行訓練。
我們計算出了求斜率的關鍵表示式。我們可以利用這個表示式對每一個訓練樣本進行訓練,之後根據訓練樣本進行更新權重。
記住權重是按照梯度的反方向進行改變。對一些特定問題,我們為了平滑改變權重將使用學習率。使用學習率避免在最小值附近的時候,超過最小值,來回震盪。我們用數學表示為:

需要更新的權重值Wjk是舊的權重值減去誤差函式斜率值。之所以減去誤差函式的梯度值是因為當斜率是正值的時候,我們想減小權重;當斜率是負值的時候我們想增加權重。符號æ是保證權重值平滑變化的一個因子,避免在靠近最小值的時候越過最小值。這個因子常常被稱為學習率。
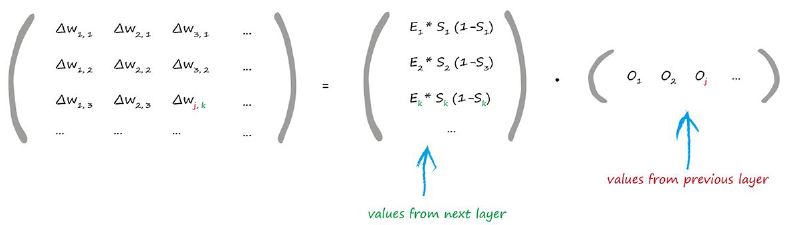
這個表示式也是可以應用於輸出層和隱藏層,而不僅僅限於隱藏層和輸出層之間。在我們計算微積分之前,我們試著用矩陣的形式表示上述表示式:
矩陣權重改變的值包括:某一層的節點j與下一層的節點k之間的權重。我們可以觀察到表示式的第一部分使用的是下一層的值,而表示式最後一部分使用的是前一層的輸出值。
上式中最後一部分是一個行向量,也即是上一層輸出結果的轉置。因此我們可以使用下面公式表示最終的結果:
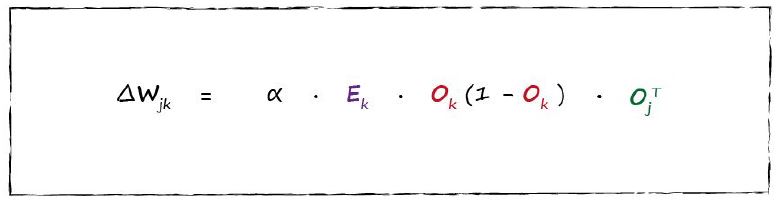
這個表示式其實不是很複雜。那些sigmoid啟用函式消失了,因為我們用節點的輸出Ok替代了它。
相關推薦
Make Your Own Neural Network(十四)-----實際上是如何更新權重(二)
神經網路的輸出是一個包含非常多權重引數的複雜函式。我們能夠使用梯度下降法求得其權重嗎?只要我們能夠使用正確的誤差函式就可以求得出神經網路中權重的引數值。神經網路的輸出本身並不是一個誤差函式。但是我們能夠輕鬆的將它轉換為誤差函式,因為誤差是訓練樣本目標值與神經網路輸出值之間的差值。如下表所示。下表標註了三個輸出
Make your own neural network(Python神經網路程式設計)一
這本書應該算我第一本深度學習的程式碼入門書了吧,之前看阿里云云棲社和景略集智都有推薦這本書就去看了, 成功建立了自己的第一個神經網路,也瞭解一些關於深度學習的內容,再加上這學期的概率論與數理統計的課, 現在再來看李大大的機器學習課程,終於能看懂LogisticsRegression概率那部分公
Make your own neural network(Python神經網路程式設計)三
前兩篇程式碼寫了初始化與查詢,知道了S函式,初始權重矩陣。以及神經網路的計算原理,總這一篇起就是最重要的神經網路的訓練了。 神經網路的訓練簡單點來講就是讓輸出的東西更加接近我們的預期。比如我們輸出的想要是1,但是輸出了-0.5,明顯不是 我們想要的。 誤差=(期望的數值)-(實際輸出),那麼我們的誤差就是
Make Your Own Neural Network(七)-----矩陣很有用
Make Your Own Neural Network構建你自己的神經網路作者:lz0499宣告:1)Make Your Own Neural Network翻譯自編寫的神經網路入門書籍。作者的目的是儘可能的少用術語和高深的數學知識,以圖文並茂的方式講解神經網路是如何工作的
Make Your Own Neural Network(八)-----利用矩陣計算三層神經網路的輸出結果
Make Your Own Neural Network構建你自己的神經網路作者:lz0499宣告:1)Make Your Own Neural Network翻譯自編寫的神經網路入門書籍。作者的目的是儘可能的少用術語和高深的數學知識,以圖文並茂的方式講解神經網路是如何工作的
Tariq Rashid+《Python神經網絡編程》中文PDF英文PDF源代碼+Make Your Own Neural Network
bubuko 彩色 簡單 ofo 簡單的 適合 識別 代碼 思想 《Python神經網絡編程》揭示神經網絡背後的概念,並介紹如何通過Python實現神經網絡。 下載:https://pan.baidu.com/s/1UTwTGYnxWquxjMueIcaNwQ 《P
How to build your own Neural Network from scratch in Python
How to build your own Neural Network from scratch in PythonA beginner’s guide to understanding the inner workings of Deep LearningMotivation: As part of my
從零開始學習html(十四)單位和值
type 當我 總結 學生 專註 bfc span blog 設置顏色 一、顏色值 1 <!DOCTYPE HTML> 2 <html> 3 <head> 4 <meta charset="utf-8"> 5
自然語言交流系統 phxnet團隊 創新實訓 個人博客 (十四)
reg ssa then soci mile pic fin lan tle 關於WikiExtractor的學習筆記: WikiExtractor是一個Python 腳本,專門用於提取和清洗Wikipedia的dump數據,支持Python 2.7 或者 Pyth
(十四)Hibernate中的多表操作(4):單向一對一
odin utf-8 lds () clas string 方式 rdb style 案例一: 註解方式實現一對一 UserBean.java package bean; import java.io.Serializable; import javax.pers
openstack controller ha測試環境搭建記錄(十四)——配置cinder(存儲節點)
nbsp 設置 ntp reason script snap rate 文件 esc 先簡述cinder存儲節點的配置: 1、IP地址是10.0.0.41; 2、主機名被設置為block1; 3、所有節點的hosts文件已添加相應條目; 4、已經配置了ntp時間同
OGG運維優化腳本(十四)-信息同步類--定義文件自動下發
ogg oracle goldengate 腳本 數據同步 shell 文件: resend.sh路徑:$HOME/ggscript/ggdef功能:該腳本為用於應對目標端因為定義文件失效導致的進程異常中斷所設計因源端業務經常未通知目標端以及系統組自行修改表結構因此設計該腳本自動生成定
CSS學習(十四)-CSS顏色之中的一個
rac 顏色 opacity bsp pac pre alpha color data- 一、理論: 1.RGB色彩模式 a.CMYK色彩模式 b.索引色彩模式 (主要用於web) c.灰度模式 d.雙色調模式 2.opacity: a.alphavalue:透明
Linux筆記(十四) - 日誌管理
關機 ron pri 內核 有用 規則 rsyslog 所有者 事件 (1)rsyslogd的服務:查看服務是否啟動:ps aux | grep rsyslogd 查看服務是否自啟動:chkconfig --list | grep rsyslog 配置文件 : /etc/r
全棧JavaScript之路(十四)HTML5 中與class屬性相關的擴充
mov html5 表示 方法 popu dom add data- token 1. getElementByClassName() :支持getElementsByClassName()方法的瀏覽器有IE 9+、Firefox 3+、Safari
如鵬網學習筆記(十四)ASP.NET
表單參數 form表單 web服務 exp 序列化 date 文字 arr 處理程序 Asp.net筆記 一、Socket類 進行網絡編程的類,可以在兩臺計算機之間進行網絡通訊 過程: 向服務器發送指令: GET /index.html HTTP
python selenium-webdriver 標簽頁切換(十四)
例子 int 道理 .get es2017 http code 按鈕 style 測試過程中有時候會遇到點擊某個按鈕或者鏈接會彈出新的窗口,這時候我們的操作的頁面還保持著最初打開頁面,但是此時我們需要操作新打開的頁面上的功能,這個時候我們需要切換一下標簽頁 。 其
設計模式(十四)——組合模式
其他 獲取 添加 http es2017 處理方式 src 所有 alt 1.描述 將對象組合成樹形結構一以表示“部分——整體”的層次結構。組合模式使用戶對單個對象和組合對象的使用具有一致性。 2.模式的使用 ·抽象組件(Component):是一個接口或抽象類,該接口定義
MySQL(十四)之數據備份與還原
pic 還原 mysql .com ace sql .cn uid 數據備份 http://pic.cnhubei.com/space.php?uid=4614&do=album&id=1719909http://pic.cnhubei.com/space.
Hadoop(十四)MapReduce原理分析
資源 並行處理 ons 描述 並發數 span col 數據分析 sub 前言 上一篇我們分析了一個MapReduce在執行中的一些細節問題,這一篇分享的是MapReduce並行處理的基本過程和原理。 Mapreduce是一個分布式運算程序的編程框架,是用戶開發