Make Your Own Neural Network

構建你自己的神經網路

作者：lz0499

宣告：

1）Make Your Own Neural Network翻譯自編寫的神經網路入門書籍。作者的目的是儘可能的少用術語和高深的數學知識，以圖文並茂的方式講解神經網路是如何工作的。任何擁有高中數學水平的人就能夠理解神經網路的工作方式。強烈推薦初學者以這本書作為神經網路入門書籍。

2）本文僅供學術交流，非商用。翻譯的初衷是一邊翻譯一邊加深對神經網路的理解。

3）由於剛剛接觸神經網路這方面的知識，翻譯過程中難免有些錯誤。若發現錯誤，還請各位前輩指正。謝謝！

4）由於工作原因，我將有選擇的按照原文的章節不定期的進行翻譯更新。

5）此屬於第一版本，若有錯誤，還需繼續修正與增刪。

目錄：

第一部分：神經網路是如何工作的

矩陣很有用

利用矩陣計算三層神經網路的輸出結果

我們之前沒有使用矩陣來表達神經網路中的各種計算，也沒有計算超過兩層的神經網路最後的結果。超過兩層的神經網路確實更有意思些，我們想知道神經網路中的中間層是如何作為第三層的輸入訊號。

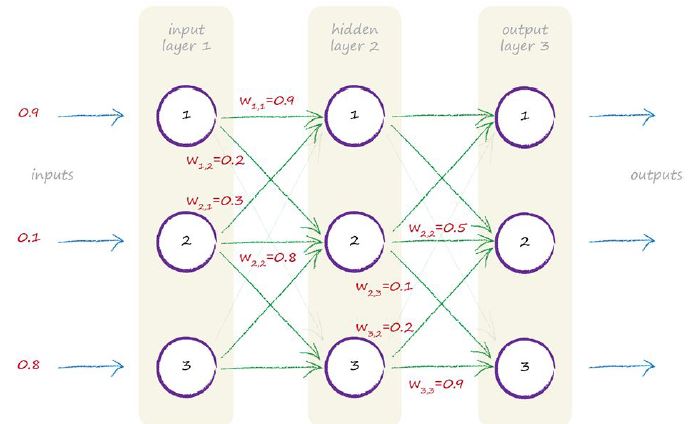
下圖表示的是每一個擁有三個節點，共三層的神經網路。為了更清晰的表示出計算結果，並沒有把所有權重都寫出來：

現在我們介紹一些計算過程中常用的專業術語。我們知道，第一層是輸入層，最後一層為輸出層。中間層我們稱之為隱藏層。這個術語聽起來有些神祕，當可惜的是隻是一個名字而已，並沒有其他太多的神祕可言。

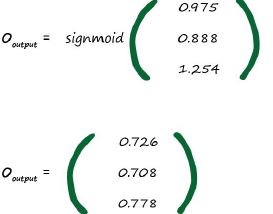
讓我們開始計算這個神經網路的輸出值。如圖所示，我們可以指導輸入訊號分辨為0.9,0.1,0.8.所以，輸入矩陣I為：

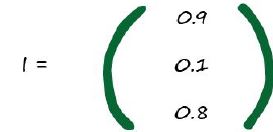
這個很簡單。第一層的輸入訊號就計算完成了。

下一層是中間隱藏層的計算了。我們知道，中間隱藏層的各個節點與輸入層的各個節點互相連線，所以這涉及到很多計算。我們不打算在一個一個單獨計算其結果，我們想利用矩陣這個強大的工作，使用矩陣乘法計算。

就像我們之前做過的一樣，輸入訊號的加權和經過sigmoid啟用函式處理之後，得到X=WI。其中I是輸入訊號矩陣，W為權重矩陣。但是W的具體值是多少呢？上述圖例中只是標出了一部分權重而不是全部權重，下圖表示了餘下的權重，我們依舊是使用隨機值表示餘下的各個權重。

我們可以從圖表中可以看出，輸入訊號的第一個節點與隱藏層的第一個節點的權重值為W1,1=0.9.同樣，輸入訊號的第二個節點與隱藏層的第二個節點的權重值為W2.2=0.8。上述圖例中並沒有標註出輸入訊號的第三個節點與隱藏層的第一個節點的權重值，我們設定為W3,1=0.4。

等等，W旁邊的（input_hiden）輸入_隱藏表示的是什麼鬼？由於表示的是輸入層和中間隱藏層之間的權重，所以我們使用輸入_隱藏下標表示這兩層之間的權重。我們需要另外一個矩陣表示隱藏層和輸出層之間的權重值，我們使用W_{隱藏層_輸出}下標表示。

下圖表示的是中間隱藏層和輸出層之間的權重值。從圖中我們可以看出，中間隱藏層的第三個節點與輸出層的第三個節點的權重值為0.9.

很好！我們已經用矩陣表示出了各個神經網路層之間的權重值。餘下的工作就是利用矩陣的乘法進行計算了。

讓我們從第一層到中間隱藏層開始計算。我們假設這一次計算出的結果用X_隱藏表示。它僅僅表示輸入到隱藏層的輸入訊號權重和，而不是最後一層的權重和。

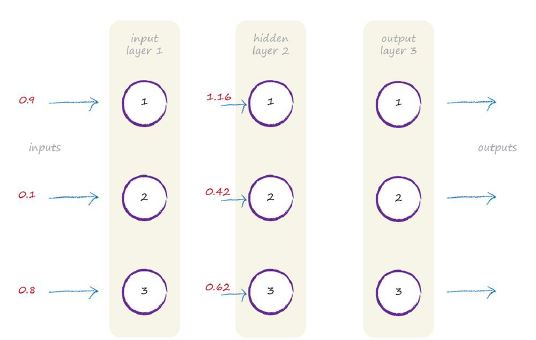
在這我們並不打算計算這兩個矩陣的相乘結果，我們想利用計算機幫助我們計算其最後的輸入結果。其結果如下：

我使用計算機計算出了其最後的結果。我們後續將會學會如何使用Python程式語言計算其結果。我們現在不打算描述如何使用計算機進行矩陣運算的，這部分內容將在本書的第二部分描述。

從輸入層到中間層我們有了其加權和為1.16,0.42,0.62。並且我們開始使用矩陣計算其加權和。這個是一個很大的進步了。

如下圖表示的是上述的計算過程。

到目前為止，一切都還不錯。但是還有更多的計算還需要做。就像自然界中的實際神經網路，求出的加權和需要經過sigmoid啟用函式的作用之後才最終輸出其結果。故有：

Sigmoid啟用函式作用於後，輸出中間隱藏層的結果為：

讓我們檢驗下是否計算得正確。Sigmoid啟用函式為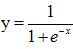，所以，當x=1.16時，這意味著最後的輸出y=1/(1+0.3135)=0.761。

從輸出結果我們可以觀察到，輸出結果都在0到1的範圍，因為sigmoid函式不會輸出超過這個範圍的數。

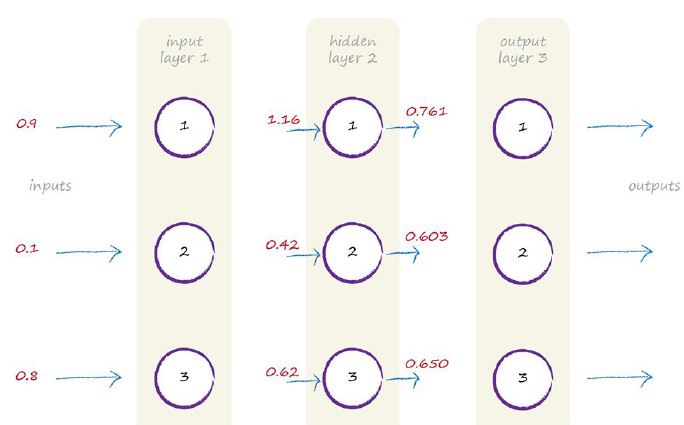
讓我們停下來，想想我們剛才發做了什麼。我們計算出了中間隱藏層的輸出結果。也即是輸入訊號經過加權求和之後再經過Sigmoid啟用函式之後的結果。讓我們更新下最新的圖表：

如果這是一個兩層的神經網路，那麼我們就已經算出這個神經網上絡的輸出結果了。實際這是一個三層的神經網路，我們還得繼續往下接著算。

如何計算出第三層網路的結果呢？過程其實同之前計算中間層輸出結果一樣。第三層的輸入訊號即是中間層的輸出結果，我們計算其加權和之後，再經過sigmoid函式輸出最後的結果。我們應該記住，無論神經網路有多少層，我們都可以按照之前那層的演算法一步一步計算：求出輸入訊號的加權和，之後再經過sigmoid啟用函式的閾值處理，輸出其最後的結果。我們不必關心神經網路中是3層還是53層，甚至是103層，其計算方法都是一樣的。

所以，讓我們按照之前的計算方法再計算第三層神經網路的輸出結果。第三層神經網路的入是第二次神經網路的輸出結果。第二層和第三層各個節點之間的權重值為，而不是我們之前計算的第一層與第二次之間的權重。所以，我們有如下式子：

最終計算出來的結果為;

我們更新計算流程結果圖：

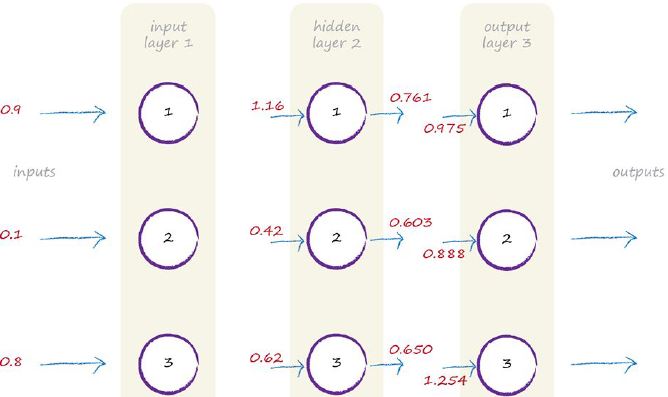
再把加權和輸入給sigmoid啟用函式有：

這就是最後的結果。輸入訊號經過神經網路之後，我們計算出了其最終的結果。如下圖所示;

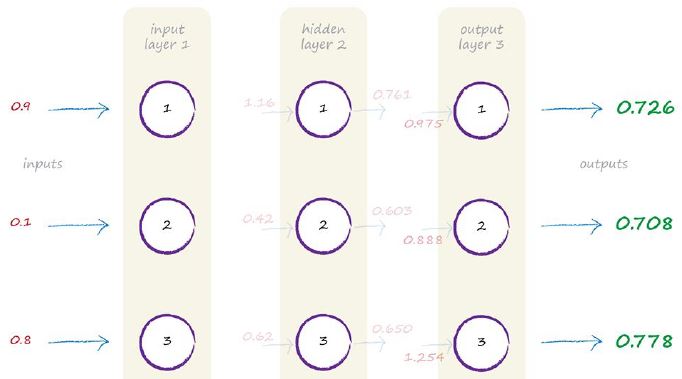
最終輸出結果分別為0.726,0.708,0.778.

下一步我們該做什麼處理呢?

下一步我們將計算出來的輸出結果與實際的訓練資料進行比較得到一個誤差。我們將利用該誤差值再進一步指導神經網路，使得輸出更為準確的輸出結果。

下一小節中，我們將慢慢道來：如何利用誤差值指導神經網路得到更為準確的輸出結果。