【數字影象處理一】RGB模型轉化為HSI模型的幾何方法推導
阿新 • • 發佈:2019-01-20
本文基於《數字影象處理》(岡薩雷斯第三版)的原網站的證明並添加了一點自己的理解,如果想要獲取作者的證明原始檔案請訪問這裡。
RGB轉換到HSI的幾何方法公式
假設RGB模型的值的取值範圍為。
HSI模型的三個分量:強度(),色調(),飽和度()的計算公式如下:
式中:
證明
HSI模型採用三稜錐還是圓錐或者圓柱都沒有影響,因為它們之間可以直接相互對映,所以三者是等價的。這裡用三角形來證明。
假設RGB值已經歸一化。歸一化方法為:
即求出各個基色的強度所佔的比例。注意到實際上代表了各個三原色的強度佔總體的比例,所以顯然滿足如下條件:
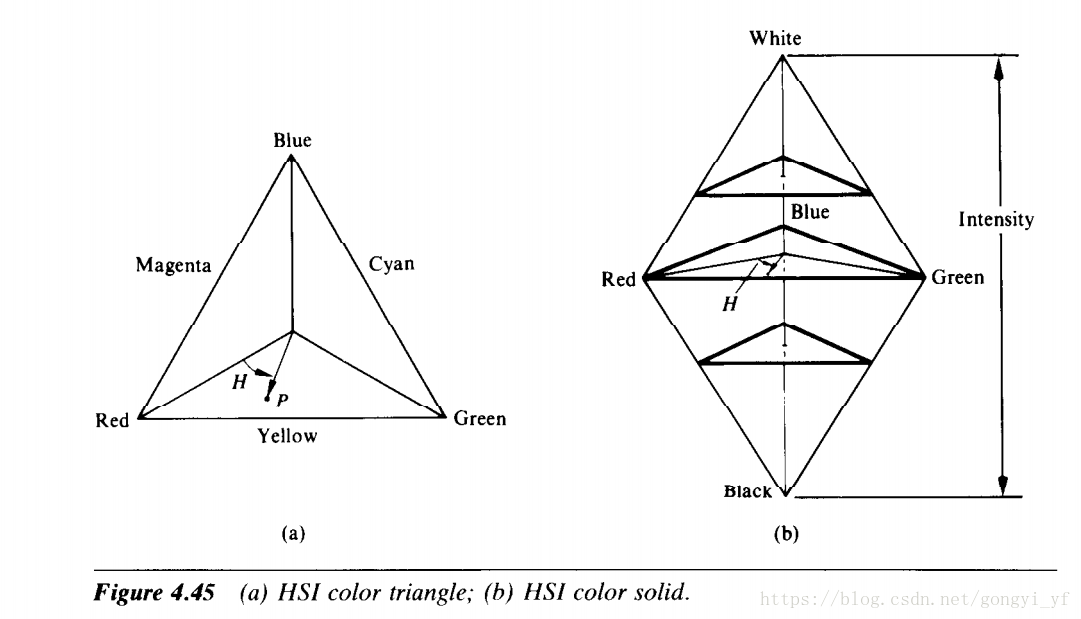
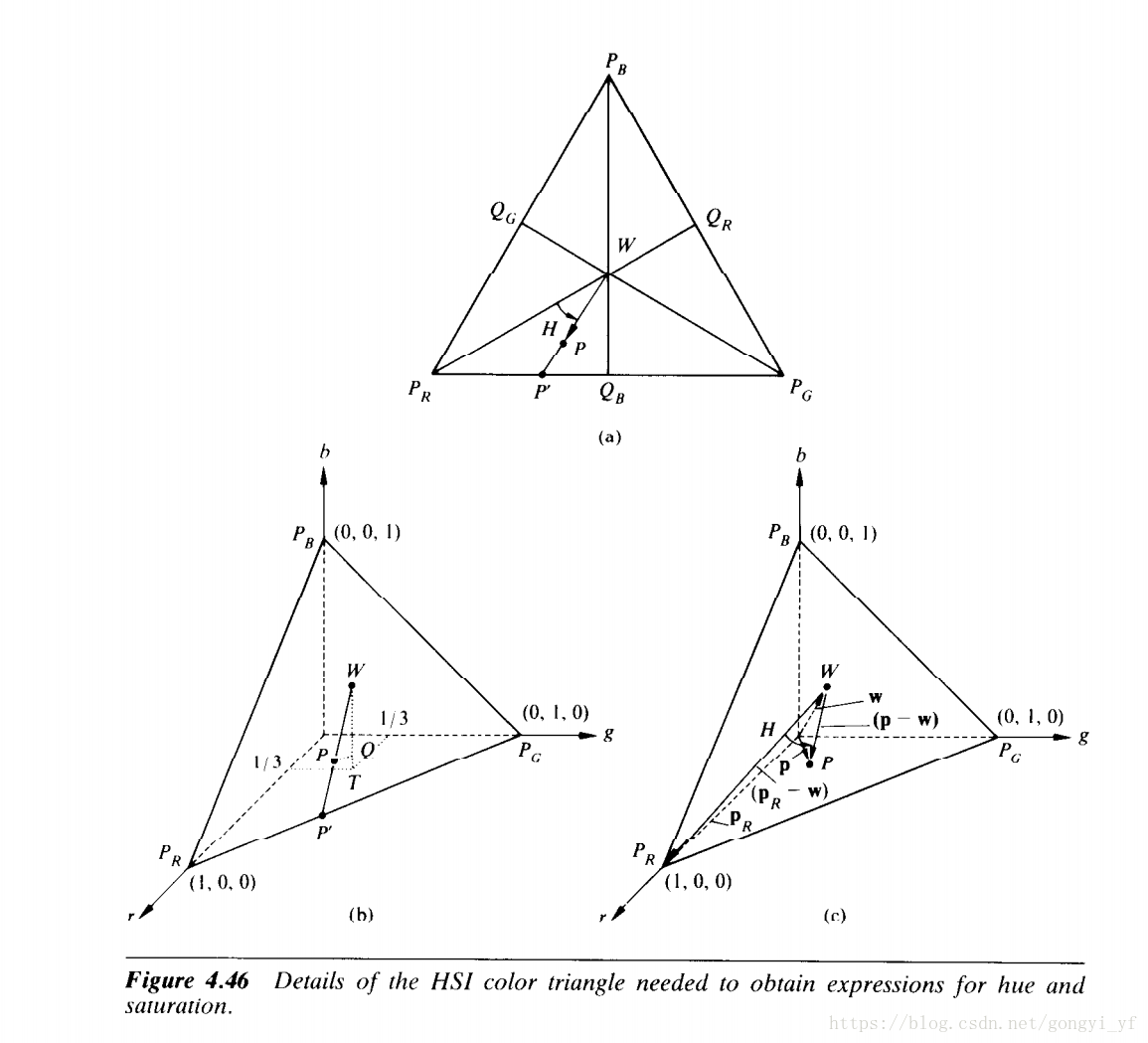
另外仔細觀察上圖中的正三稜錐上的面,該平面上的任意一點都代表了值值值滿足比例條件的色點。比如該平面上的點代表的所的點。
另外給出幾條假設和顯然的前提條件:
(1)點的座標是,因為正三角形。
(2)設三角形上點的座標為。
(3)設連線座標原點和W的向量為&w&,同樣的有。
(4)圖中的直線
