漢諾塔問題是源於印度一個古老傳說的益智玩具。大梵天創造世界的時候做了三根金剛石柱子，在一根柱子上從下往上按照大小順序摞著64片黃金圓盤。大梵天命令婆羅門把圓盤從下面開始按大小順序重新擺放在另一根柱子上。並且規定，在小圓盤上不能放大圓盤，在三根柱子之間一次只能移動一個圓盤。

如果考慮一下把64片金盤，由一根柱子上移到另一根柱子上，並且始終保持上小下大的順序。這需要多少次移動呢？這裡需要遞迴的方法。假設有n片，移動最少次數是f(n).顯然f(1)=1,f(2)=3,f(3)=7,且f(k+1)=2*f(k)+1。此後不難證明f(n)=2^n-1。

在本文中，將討論用遞迴和非遞迴的方法來解決漢諾塔問題。

1、 通過遞迴實現漢諾塔問題的求解

設f(n)為將n片圓盤所在塔全部移動到另一塔最少總次數；由遞迴演算法可知：f(1) = 1;當n>1時，f(n)   = f(n-1) +  1 + f(n-1)。f(n) = 把上面n-1片圓盤移動到中間塔最少總次數f(n-1) + 把第n片圓盤移動到目標塔+ 把中間盤的n-1片圓盤移動到目標塔最少總次數為f(n-1)。由數學計算可得：f(n)=2^n-1。(n>0)。此演算法的遞迴程式碼實現如下所示：

#include <fstream>
#include <iostream>
#include<time.h>
using namespace std;
void Move(int n,char x,char y)
{
   cout<<"把"<<n<<"號從"<<x<<"挪動到"<<y<<endl;
}
void Hannoi(int n,char a,char b,char c)
{
      if(n==1)
              Move(1,a,c);
    else
    {
          Hannoi(n-1,a,c,b);
            Move(n,a,c);
            Hannoi(n-1,b,a,c);
    }
}
int main()
{
  int n;
  cout<<"請輸入要求解的漢諾塔的階數： ";
  cin>>n;
  clock_t start,finish;
  start = clock();
    cout<<"以下是7層漢諾塔的解法:"<<endl;
    Hannoi(n,'a','b','c');
    cout<<"輸出完畢！"<<endl;
  finish = clock();
  printf("解決此 %d 階漢諾塔所需的時間為：%.2f ms\n",n,(double)(finish-start));
  system("pause");
    return 0;
}
 

2、 通過非遞迴的思想來實現漢諾塔問題的求解

漢諾塔的非遞迴演算法描述如下：

首先容易證明，當盤子的個數為n時，移動的次數應等於2^n - 1。

一位美國學者發現一種出人意料的方法，只要輪流進行兩步操作就可以了。

首先把三根柱子按順序排成品字型，把所有的圓盤按從大到小的順序放在柱子A上。

根據圓盤的數量確定柱子的排放順序：若n為偶數，按順時針方向依次擺放 A B C；

若n為奇數，按順時針方向依次擺放 A C B。

（1）按順時針方向把圓盤1從現在的柱子移動到下一根柱子，即當n為偶數時，若圓盤1在柱子A，則把它移動到B；

若圓盤1在柱子B，則把它移動到C；若圓盤1在柱子C，則把它移動到A。

（2）接著，把另外兩根柱子上可以移動的圓盤移動到新的柱子上。

即把非空柱子上的圓盤移動到空柱子上，當兩根柱子都非空時，移動較小的圓盤

這一步沒有明確規定移動哪個圓盤，你可能以為會有多種可能性，其實不然，可實施的行動是唯一的。

（3）反覆進行（1）（2）操作，最後就能按規定完成漢諾塔的移動。

該演算法的實現程式碼如下：

#include <iostream>
#include<time.h>
using namespace std;
//圓盤的個數最多為64
const int MAX = 64;
//用來表示每根柱子的資訊
struct st{
     int s[MAX]; //柱子上的圓盤儲存情況
     int top; //棧頂，用來最上面的圓盤
     char name; //柱子的名字，可以是A，B，C中的一個
     int Top()//取棧頂元素
     {
           return s[top];
     }
     int Pop()//出棧
     {
           return s[top--];
     }
     void Push(int x)//入棧
     {
           s[++top] = x;
     }
} ;
 
long Pow(int x, int y); //計算x^y
void Creat(st ta[], int n); //給結構陣列設定初值
void Hannuota(st ta[], long max); //移動漢諾塔的主要函式
int main(void)
{
     clock_t start,finish;
           int n;
           cout<<"請輸入漢諾塔的階數：";
     cin >> n; //輸入圓盤的個數
           start = clock();
     st ta[3]; //三根柱子的資訊用結構陣列儲存
     Creat(ta, n); //給結構陣列設定初值
     long max = Pow(2, n) - 1;//動的次數應等於2^n - 1
     Hannuota(ta, max);//移動漢諾塔的主要函式
           finish = clock();
           printf("解決此 %d 階漢諾塔所需的時間為：%.2f ms\n",n,(double)(finish-start));
     system("pause");
     return 0;
}
void Creat(st ta[], int n)
{
     ta[0].name = 'A';
     ta[0].top = n-1;
    //把所有的圓盤按從大到小的順序放在柱子A上
     for (int i=0; i<n; i++)
           ta[0].s[i] = n - i;
     //柱子B，C上開始沒有沒有圓盤
     ta[1].top = ta[2].top = 0;
     for (int i=0; i<n; i++)
           ta[1].s[i] = ta[2].s[i] = 0;
    //若n為偶數，按順時針方向依次擺放 A B C
     if (n%2 == 0)
     {
           ta[1].name = 'B';
           ta[2].name = 'C';
     }
     else  //若n為奇數，按順時針方向依次擺放 A C B
     {
           ta[1].name = 'C';
           ta[2].name = 'B';
     }
}
 
long Pow(int x, int y)
{
     long sum = 1;
     for (int i=0; i<y; i++)
           sum *= x;
     return sum;
}
 
void Hannuota(st ta[], long max)
{
  intk = 0; //累計移動的次數
  inti = 0;
  intch;
 while (k < max)
  {
   //按順時針方向把圓盤1從現在的柱子移動到下一根柱子
   ch = ta[i%3].Pop();
  ta[(i+1)%3].Push(ch);
  cout << ++k << ": " <<
        "Move disk " << ch << " from " <<ta[i%3].name <<
        " to " << ta[(i+1)%3].name << endl;
  i++;
   //把另外兩根柱子上可以移動的圓盤移動到新的柱子上
   if(k < max)
  {    
   //把非空柱子上的圓盤移動到空柱子上，當兩根柱子都為空時，移動較小的圓盤
   if (ta[(i+1)%3].Top() == 0 ||
       ta[(i-1)%3].Top() > 0 &&
       ta[(i+1)%3].Top() > ta[(i-1)%3].Top())
   {
       ch =  ta[(i-1)%3].Pop();
       ta[(i+1)%3].Push(ch);
       cout << ++k << ": " << "Move disk"
            << ch << " from " << ta[(i-1)%3].name
            << " to " << ta[(i+1)%3].name << endl;
    }
   else
    {
      ch =  ta[(i+1)%3].Pop();
      ta[(i-1)%3].Push(ch);
      cout << ++k << ": " << "Move disk"
           << ch << " from " << ta[(i+1)%3].name
           << " to " << ta[(i-1)%3].name << endl;
    }
 }
}
}

3、 實驗結果及分析（測試時以7階漢諾塔為例）

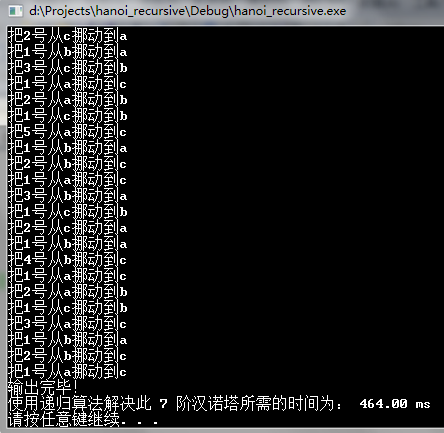
使用遞迴演算法時執行的情況：

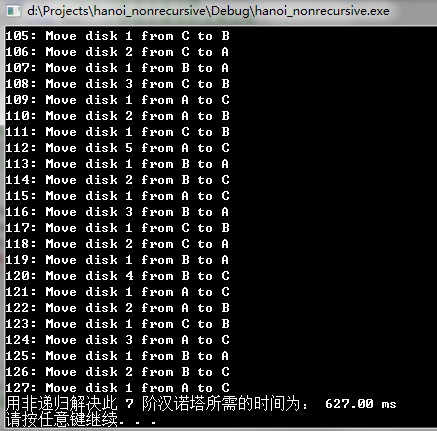
使用非遞迴演算法時執行的情況：

      從實驗結果可以看出，與n皇后問題不同，對於漢諾塔問題的求解，當使用遞迴的方法來解決時它的時間複雜度比非遞迴的方法要好。而且，使用遞迴演算法寫程式碼時更容易理解。通過對於漢諾塔問題非遞迴與遞迴方法的對比可以得出結論：有的時候使用的遞迴的方法對於問題的求解不僅更能使人容易理解，而且效率更高。我們在以後編程式碼時也應該注意遞迴方法的使用。