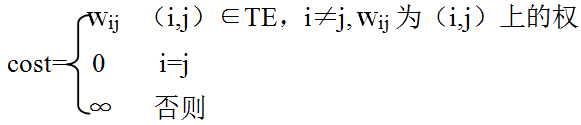一、實驗目的

1．掌握圖的相關概念。

2．掌握用鄰接矩陣和鄰接表的方法描述圖的儲存結構。

3．掌握圖的深度優先搜尋和廣度優先搜尋遍歷的方法及其計算機的實現。

4．理解最小生成樹的有關演算法

二、實驗內容

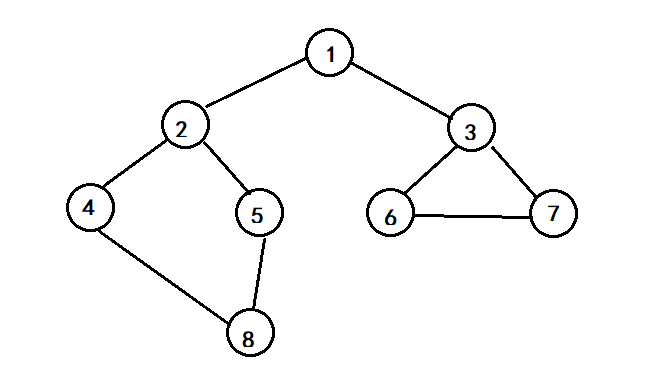
1．用鄰接表作為圖的儲存結構建立一個圖，並對此圖分別進行深度優先搜尋和廣度優先搜尋遍歷。

2．用鄰接矩陣作為圖的儲存結構建立一個網，並構造該網的最小生成樹（選做）。

三、實驗要求

1、用鄰接表作為圖的儲存結構建立一個圖，並對此圖分別進行深度優先搜尋和廣度優先搜尋遍歷。

（1）輸入無向圖的頂點數、邊數及各條邊的頂點對，建立用鄰接表表示的無向圖。

（2）對圖進行深度優先搜尋和廣度優先搜尋遍歷，並分別輸出其遍歷序列。

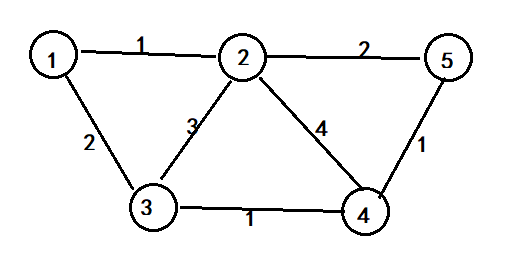
2、用鄰接矩陣作為圖的儲存結構建立一個網，構造該網的最小生成樹。

（1）輸入無向圖的頂點數、邊數及各條邊的頂點序號對和邊上的權值，建立用鄰接矩陣表示的無向網。

（2）用Prim演算法構造該無向網的最小生成樹。

（3）在實現普里姆演算法時，採用鄰接矩陣cost表示給定的無向網，矩陣元素定義為：

四、詳細程式清單

//1.鄰接表、DFS和BFS 
#include <stdio.h>  
#include <stdlib.h>  
  
#define  MAX_VERTEX_NUM 30  
 
typedef struct arcnode//邊表結點 
    {  	
	 	int adjvex;//鄰接點域,儲存該頂點對應的下標 
      	struct arcnode *nextarc;//鏈域,指向下一個鄰接點 
	} arcnode,*Linkarc; 
  
typedef struct//頂點表節點  
{
   arcnode *firstarc;//邊表頭指標
   int tag;//0代表未被訪問，1代表已被訪問
}vexnode; 
  
typedef struct//頂點陣列 
{
   	vexnode adjlist[MAX_VERTEX_NUM];
    int vexnum,arcnum;//圖中當前頂點數和邊數
}Algraph;  

typedef struct{//順序佇列 
	int *base;
	int front;
	int rear;
}Sqqueue;
Sqqueue Q;

void Initqueue(Sqqueue&Q)//初始化佇列 
{
	Q.base=(int*)malloc(sizeof(int));
	Q.front=Q.rear=0;
}

void Enqueue(Sqqueue &Q, int e)//入佇列 
{ 
    Q.base[Q.rear]=e;
	Q.rear=Q.rear+1;
} 

int Dequeue(Sqqueue &Q)//出佇列 
{
	int e;	
    e=Q.base[Q.front];
    Q.front=Q.front+1;
    return e;
}

void CreateUDG(Algraph*G)//建立無向圖的鄰接表 
{  
    int i,j,k,w,v,s,d;
	Linkarc p,q; 
    printf("輸入頂點數：");  
    scanf("%d",&G->vexnum);  
	printf("輸入邊數：");  
    scanf("%d",&G->arcnum);   
    for (i=1;i<=G->vexnum;i++)//頂點表 
    { 
	   G->adjlist[i].tag=0;//初始化為0 
       G->adjlist[i].firstarc=NULL;
    }  
    for (k=1;k<=G->arcnum;k++)//頂點所包含的連結串列
    {  
        printf("輸入邊%d的一對頂點：",k);  
		scanf("%d%d",&s,&d);
        p=(arcnode*)malloc(sizeof(arcnode)); 
        q=(arcnode*)malloc(sizeof(arcnode));
        p->adjvex=d;   q->adjvex=s;		 
        p->nextarc=G->adjlist[s].firstarc;G->adjlist[s].firstarc=p;
        q->nextarc=G->adjlist[d].firstarc;G->adjlist[d].firstarc=q;
    }
}

void Dfs(Algraph*G,int v)  //深度優先遍歷
{
	int w;
	arcnode *p;
	printf("%5d",v);
	G->adjlist[v].tag=1;
	p=G->adjlist[v].firstarc;
	while(p!=NULL)
	{
		w=p->adjvex;
      	if(G->adjlist[w].tag==0)
        Dfs(G,w);
      	p=p->nextarc;
    }
}

void Bfs(Algraph*G,int v) //廣度優先遍歷
{
	int v1,w;
    arcnode *p;
    Q.base=NULL;
    Initqueue(Q);
    printf("%5d",v);
    G->adjlist[v].tag=1;
    Enqueue(Q,v);
    while(Q.front!=Q.rear)
	{
		v1=Dequeue(Q);
      	p=G->adjlist[v1].firstarc;
        while(p!=NULL)
        {
			w=p->adjvex;
	    	if(G->adjlist[w].tag==0)
	        {
				printf("%5d",w);
		        G->adjlist[w].tag=1;
	            Enqueue(Q,w);
	        }
            p=p->nextarc;          
        }
     }
}

int main()  
{
	int v=1;//題目沒有規定，預設從1結點開始遍歷 
    Algraph*G=(Algraph*)malloc(sizeof(Algraph));  
    CreateUDG(G); 
    printf("深度優先遍歷為：");
    Dfs(G,v);
    for (int i=1;i<=G->vexnum;i++)
	G->adjlist[i].tag=0;//將全部tag重新賦0 
    printf("\n廣度優先遍歷為：");
    Bfs(G,v);
    return 0;
}  
 

//2.鄰接矩陣和prim 
#include<stdio.h>
#include<stdlib.h>
 
#define INFINITY 0x7FFFFFFF //定義最大值∞
#define MAX_VEX_NUM 50
#define MAX_VERTEX_NUM 2500

typedef struct  
{
	int vexs[MAX_VERTEX_NUM];//頂點名
	int cost[MAX_VEX_NUM][MAX_VEX_NUM];//各邊權值 
	int vexnum,arcnum;
}Mgraph;
Mgraph G;

typedef struct  ///輔助陣列
{
	int lowcost;  //權值
    int closest;  //點序號
}Closedge;
Closedge closedge[MAX_VEX_NUM];

int LocateVex(Mgraph &G,int x)
{
	for(int i=1;i<=G.vexnum;i++)
	{
		if(x==G.vexs[i])
		return i;
	}
}

void CreateUDN(Mgraph &G) //在鄰接矩陣儲存結構上，構造無向網G
{
	int i,j,k,w;
	int v1,v2;
	printf("輸入頂點數和邊數：");
	scanf("%d%d",&G.vexnum,&G.arcnum);//讀入頂點和邊數目
	printf("輸入各頂點名\n");	
	for(i=1;i<=G.vexnum;i++)//頂點名 
	{
		printf("點%d：",i);
		scanf("%d",&G.vexs[i]);
	}
	for(i=1;i<=G.vexnum;i++) //鄰接矩陣初始化
	   for(j=1;j<=G.vexnum;j++)
	   {
	   		if(i==j) G.cost[i][j]=0; 
	   		else G.cost[i][j]=INFINITY; 
	   }
	printf("輸入各頂點對和權值\n");
	for(k=1;k<=G.arcnum;k++)//構造鄰接矩陣
	{
		scanf("%d%d%d",&v1,&v2,&w);
		i=LocateVex(G,v1); j=LocateVex(G,v2);//確定v1、v2在圖中的位置
		G.cost[i][j]=w;
		G.cost[j][i]=G.cost[i][j];
	} 
}

void Prim(Mgraph G,int v)
{
    int i,j,k,min,x,y;
    int sum=0;//總權值 
    x=LocateVex(G,v); 
    for(i=1;i<=G.vexnum;i++)//初始化陣列closedge
	{
		if(i!=x)
		{
			closedge[i].lowcost=G.cost[x][i];
        	closedge[i].closest=G.vexs[x];
    	}
	} 
    closedge[x].lowcost=0; //初始U={v}
    for(i=1;i<G.vexnum;i++)
    {
        min=INFINITY;
        for(j=1;j<=G.vexnum;j++)
        if(closedge[j].lowcost!=0&&closedge[j].lowcost<min)
        {
			min=closedge[j].lowcost;
	        k=j;
        }
        printf("%d-%d:%d\n",closedge[k].closest,k,min); //輸出最小邊
        sum+=min;
        closedge[k].lowcost=0;
        for(j=1;j<=G.vexnum;j++)
	    if (closedge[j].lowcost!=0&&G.cost[k][j]<closedge[j].lowcost)
	    {
	   		closedge[j].lowcost=G.cost[k][j];
	    	closedge[j].closest=k;
        } 
    }
    printf("總權值為%d\n",sum);
}

int main()
{
	int v=1;//題目沒有規定，預設從A結點開始遍歷 
	CreateUDN(G);
	printf("最小生成樹為：\n"); 
	Prim(G,v);
}
 

五、程式執行結果

1. 鄰接表、DFS和BFS  

//其實遍歷結果有很多種，不一定是這個，我湊巧和書上一樣了。。。

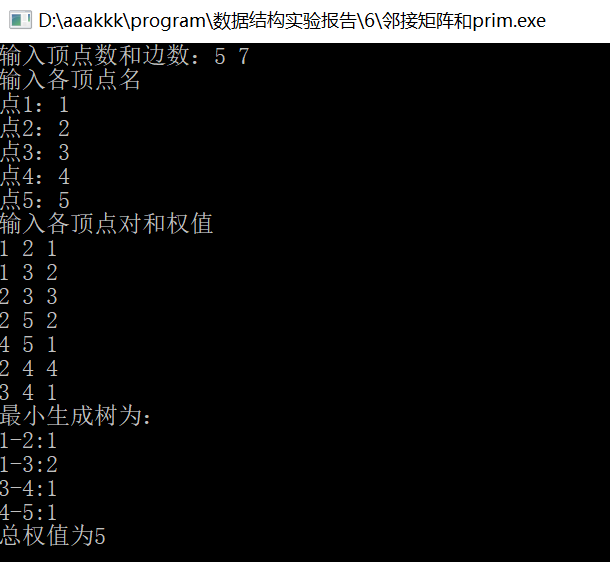
2. 鄰接矩陣和prim

六、實驗心得體會
1. 在儲存稀疏圖的時候，用鄰接表比鄰接矩陣更省空間。
2. 在鄰接表上容易找到任一頂點的第一個鄰接點和下一個鄰接點，但要判斷任一兩個點之間是否相連，則需搜尋第i或第j個連結串列，此時用鄰接矩陣更方便。
3. DFS和BFS的遍歷結果不一定唯一。
4. C語言是沒有無窮大的，因此，一般用一個很大的數來近似替代無窮大：#define INFINITY 0x7FFFFFFF。
5. Prim演算法的時間複雜度為O(n²)，與網的邊數無關，於是適合於稠密圖；而Kruskal演算法的時間主要取決於邊數，於是更適合於稀疏圖。