在講義《線性迴歸、梯度下降》和《邏輯迴歸》中我們提到可以用梯度下降或梯度上升的方式求解θ。在本文中將講解另一種求解θ的方法：牛頓方法（Newton's method）。

牛頓方法（Newton's method）

     邏輯迴歸中利用Sigmoid函式g(z)和梯度上升來最大化ℓ(θ)。現在我們討論另一個最大化ℓ(θ)的演算法----牛頓方法。

     牛頓方法是使用迭代的方法尋找使f(θ)=0的θ值，在這裡θ是一個真實的值，不是一個引數，只不過θ的真正取值不確定。牛頓方法數學表示式為：

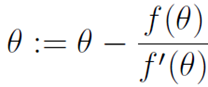
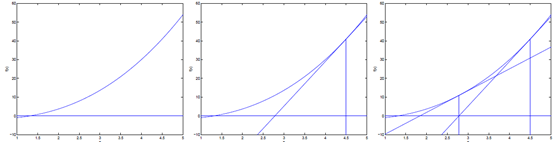
      牛頓方法簡單的理解方式為：先隨機選一個點，然後求出f在該點的切線，即f在該點的導數。該切線等於0的點，即該切線與x軸相交的點為下一次迭代的值。直至逼近f等於0的點。過程如下圖：

牛頓方法最大化Likelihood

      牛頓方法提供了一種尋找f(θ)=0的θ值的方法。怎麼用於最大化似然函式ℓ (θ)呢？ℓ的最大值對應點處的一階導數ℓ'(θ)為零。所以讓f(θ) = ℓ'(θ)，最大化ℓ (θ)就可以轉化為：用牛頓方法求ℓ'(θ)=0的θ的問題。由牛頓方法的表示式，θ的迭代更新公式為：

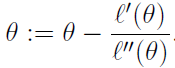
牛頓-拉夫森迭代法（Newton-Raphson method）

     邏輯迴歸中θ是一個向量，所以我們把上面的表示式推廣到多維的情況就是牛頓-拉夫森迭代法（Newton-Raphson method），表示式如下：

      表示式中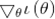表示的ℓ(θ)對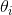的偏導數；H是一個n*n的矩陣，稱為Hessian矩陣。Hessian矩陣的表示式為：

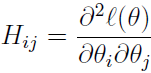
牛頓方法VS梯度下降

      如下圖是一個最小化一個目標方程的例子，紅色曲線是利用牛頓法迭代求解，綠色曲線是利用梯度下降法求解：

      牛頓方法通常比梯度下降收斂速度快，迭代次數也少。

      但因為要計算Hessian矩陣的逆，所以每次迭代計算量比較大。當Hessian矩陣不是很大時牛頓方法要優於梯度下降。