牛頓法(Newton‘s method)和擬牛頓法(quasi Newton method)
阿新 • • 發佈:2018-12-11
簡述
在看伊恩·古德費洛的深度學習,4.3節基於梯度的優化方法時提到
僅使用梯度資訊的優化演算法稱為 一階優化演算法 ,如梯度下降。
使用Hessian矩陣的優化演算法稱為 二階最優化演算法 ,如牛頓法。
牛頓法和擬牛頓法時求解無約束最優化問題的常用方法,收斂速度快。
牛頓法是迭代演算法,每一步需要求解目標函式的海賽矩陣的逆矩陣,計算比較複雜;
擬牛頓法通過正定矩陣近似海賽矩陣的逆矩陣或海賽矩陣,簡化這一計算過程。
下面記錄一下對牛頓法的一點理解
牛頓法(Newton‘s method)
儲備知識:泰勒展開式
當=0時就是麥克勞倫展開式
以及常見函式的展開式
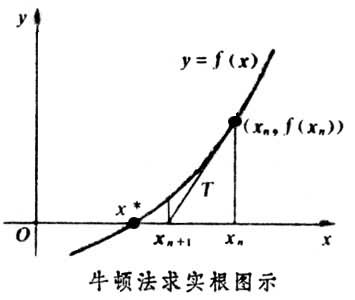
應用A:求解方程
將利用泰勒公式在處展開到一階
令=0,求解得到
比
更接近於
=0
可以推出
應用B:最優化
將利用泰勒公式展開到二階
當趨向於0時,
求解
得到迭代公式 ,n=0,1,2……
可以看到牛頓法的迭代步長為
常見的最優化方法有:梯度下降法、牛頓法、擬牛頓法、共軛梯度法等等
如下圖紅色曲線是利用牛頓法迭代求解;綠色曲線是利用梯度下降法迭代求解。
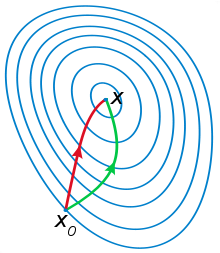
從本質上來講,最優化求解問題的迭代形式都是
最優化問題的標準形式是:求目標函式最小值,只要每次迭代沿著下降的方向可以逐漸達到最優
參考博文:Newton法(牛頓法 Newton Method)
待補充



