最短路徑演算法——Dijkstra演算法的JS實現
一、Dijkstra演算法的思路
Dijkstra演算法是針對單源點求最短路徑的演算法。
其主要思路如下:
1. 將頂點分為兩部分:已經知道當前最短路徑的頂點集合Q和無法到達頂點集合R。
2. 定義一個距離陣列(distance)記錄源點到各頂點的距離,下標表示頂點,元素值為距離。源點(start)到自身的距離為0,源點無法到達的頂點的距離就是一個大數(比如Infinity)。
3. 以距離陣列中值為非Infinity的頂點V為中轉跳點,假設V跳轉至頂點W的距離加上頂點V至源點的距離還小於頂點W至源點的距離,那麼就可以更新頂點W至源點的距離。即下面distance[V] + matrix[V][W] < distance[W],那麼distance[W] = distance[V] + matrix[V][W]。
4. 重複上一步驟,即遍歷距離陣列,同時無法到達頂點集合R為空。
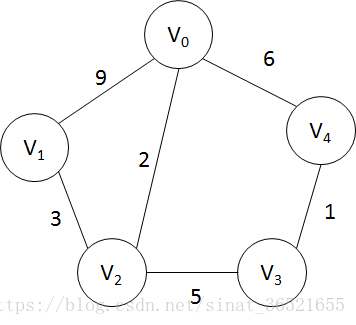
二、具體例子
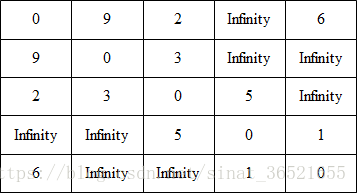
它的鄰接矩陣如下:
求解步驟
第一步:假設源點為V0,那麼目前最短路徑的頂點集合Q中就只有{V0}和無法到達頂點集合R中有{V1, V2, V3, V4}
第二步:初始化distance陣列,就是下面這樣
第三步:以distance陣列中值為非Infinity的頂點為中轉跳點,這一步就是V0,依照如果distance[V] + matrix[V][W] < distance[W],那麼distance[W] = distance[V] + matrix[V][W]的規則,distance陣列就會變成下面這樣,同時集合Q變成了{V0, V1, V2, V4},集合R變成了{V3}
第四步:因為集合R中還有1個頂點,所以重複第三步的方法,然後變成以V1為中轉跳點,但是以V1為中轉頂點都不滿足distance[V] + matrix[V][W] < distance[W],所以沒更新distance和兩個集合
第五步:因為集合R中還有1個頂點,所以重複第三步的方法,此時變成以V2為中轉跳點,然後發現V0到達V3的距離可以更新,因為2 + 3 < 9,所以distance更新,集合也更新。
之後同理,遍歷完distance之後,輸出
三、程式碼實現
這個程式碼沒有考慮權值為負數的情況,還沒驗證負數的情況,目前是按照權值為正數實現的,之後考慮完善。
同時這是針對單源點求最短路徑,如果求全圖各頂點的最短路徑,只需要遍歷頂點然後使用Dijkstra演算法,這樣算上Dijkstra演算法本身的時間複雜度,總的複雜度會是O(n^3)。
/**
* Dijkstra演算法:單源最短路徑
* 思路:
* 1. 將頂點分為兩部分:已經知道當前最短路徑的頂點集合Q和無法到達頂點集合R。
* 2. 定義一個距離陣列(distance)記錄源點到各頂點的距離,下標表示頂點,元素值為距離。源點(start)到自身的距離為0,源點無法到達的頂點的距離就是一個大數(比如Infinity)。
* 3. 以距離陣列中值為非Infinity的頂點V為中轉跳點,假設V跳轉至頂點W的距離加上頂點V至源點的距離還小於頂點W至源點的距離,那麼就可以更新頂點W至源點的距離。即下面distance[V] + matrix[V][W] < distance[W],那麼distance[W] = distance[V] + matrix[V][W]。
* 4. 重複上一步驟,即遍歷距離陣列,同時無法到達頂點集合R為空。
*
* @param matrix 鄰接矩陣,表示圖
* @param start 起點
*
*
*
* 如果求全圖各頂點作為源點的全部最短路徑,則遍歷使用Dijkstra演算法即可,不過時間複雜度就變成O(n^3)了
* */
function Dijkstra(matrix, start = 0) {
const rows = matrix.length,//rows和cols一樣,其實就是頂點個數
cols = matrix[0].length;
if(rows !== cols || start >= rows) return new Error("鄰接矩陣錯誤或者源點錯誤");
//初始化distance
const distance = new Array(rows).fill(Infinity);
distance[start] = 0;
for(let i = 0; i < rows; i++) {
//達到不了的頂點不能作為中轉跳點
if(distance[i] < Infinity) {
for(let j = 0; j < cols; j++) {
//比如通過比較distance[i] + matrix[i][j]和distance[j]的大小來決定是否更新distance[j]。
if(matrix[i][j] + distance[i] < distance[j]) {
distance[j] = matrix[i][j] + distance[i];
}
}
console.log(distance);
}
}
return distance;
}
/**
* 鄰接矩陣
* 值為頂點與頂點之間邊的權值,0表示無自環,一個大數表示無邊(比如10000)
* */
const MAX_INTEGER = Infinity;//沒有邊或者有向圖中無法到達
const MIN_INTEGER = 0;//沒有自環
const matrix= [
[MIN_INTEGER, 9, 2, MAX_INTEGER, 6],
[9, MIN_INTEGER, 3, MAX_INTEGER, MAX_INTEGER],
[2, 3, MIN_INTEGER, 5, MAX_INTEGER],
[MAX_INTEGER, MAX_INTEGER, 5, MIN_INTEGER, 1],
[6, MAX_INTEGER, MAX_INTEGER, 1, MIN_INTEGER]
];
console.log(Dijkstra(matrix, 0));//[ 0, 5, 2, 7, 6 ]相關推薦
最短路徑之Dijkstra演算法 C語言實現
Dijkstra演算法(單源點路徑演算法,要求:圖中不存在負權值邊): 步驟: a. 初始時,S只包含源點,即S={v},v的距離為0。U包含除v外的其他頂點,即: U={其餘頂點},若v與U中頂點u有邊,則u的距離設定為相應的權值,若u v之間不存在邊,則
最短路徑之Dijkstra演算法的概念與實現
基本概念 要找出最短路徑,其實就是從起點遍歷所有能到達的頂點,然後計算他們的權重。Dijkstra演算法核心在於邊的鬆弛(relax),可以想象成一根繃緊的橡皮筋,讓它放鬆下來。即是計算源點(s)經過當前點(v)到目標點(w)的權重,如果比目標點(w)之前的權
最短路徑之Dijkstra演算法Java實現
Dijkstra演算法步驟 以下圖為例,求頂點v1到其他頂點的最短路徑 初始化dis陣列,怎麼初始化呢?v1→v1設定為0,不能直接到達的設定為無窮大,能直接到達的附權值,並且定義集合T,初始
單元最短路徑問題---Dijkstra演算法
最短路徑—Dijkstra演算法和Floyd演算法(理解):https://blog.csdn.net/m0_37345402/article/details/76695930 理解最短路徑——迪傑斯特拉(dijkstra)演算法:https://www.cnblogs.com/iambupu/
最短路徑問題---Dijkstra演算法詳解
前言 Nobody can go back and start a new beginning,but anyone can start today and make a new ending. Name:Willam Time:2017/3/8 1、最短路徑問題介紹
A.pro讀演算法の11:最短路徑之Dijkstra演算法
此文是獻給OIer看的。講的東西比較基礎(其實我理解Dijkstra花了很長時間)。NOIP2018結束約有1個月了,但是我們仍要繼續前進,為NOIP2019做準備。本節學習Dijkstra的演算法思想和實現,以及優先佇列和堆優化。線段樹也可以做到優化,甚至可能還更快,但是我太弱了不會。。
最短路徑問題-Dijkstra演算法
前言: 最短路徑演算法用於計算一個節點到其他所有節點的最短路徑。主要特點是以起始點為中心向外層層擴充套件,直到擴充套件到終點為止。 最短路徑問題是圖論研究中的一個經典演算法問題,是尋找圖(由結點和路徑組成的)中兩結點之間的最短路徑。 文章為了通俗易懂,避免使用一些複雜詞
Java資料結構:單源最短路徑問題---Dijkstra演算法
嚶擊長空 如圖: 思路:先任意找一個根節點,然後開始迴圈找連線該點所有邊,然後找到權值最小的一項,標記被訪問,然後再次迴圈找除了根節點和被訪問過的結點的邊,找到權值最小的。具體開註釋,非常詳細喲。 上程式碼: public void shortesPath(int i) { in
最短路徑之Dijkstra演算法
Dijkstra(迪傑斯特拉)演算法是典型的最短路徑路由演算法,用於計算一個節點到其他所有節點的最短路徑。主要特點是以起始點為中心向外層層擴充套件,直到擴充套件到終點為止(BFS、prime演算法都有類似思想)。Dijkstra演算法能得出最短路徑的最優解,但由於它遍歷計算
圖結構練習——最短路徑(Dijkstra演算法)
think: 1注意重複邊的覆蓋 2注意map陣列的初始化 3注意dist陣列的初始化 圖結構練習——最短路徑 Time Limit: 1000MS Memory Limit: 65536KB Problem Description 給定一個
獲取多條最短路徑的Dijkstra演算法
Dijkstra演算法是單源最短路徑經典演算法,一般用於所有邊的權為非負數的情況下,有向圖和無向圖均可。 效率方面:儲存圖模型的資料結構有很多種,使用鄰接矩陣的話其空間複雜度都為O(E^2)。而如果是稀疏圖,使用鄰接連結串列更划算,空間複雜度為O(V+E)。在
【演算法導論】單源最短路徑之Dijkstra演算法
Dijkstra演算法解決了有向圖上帶正權值的單源最短路徑問題,其執行時間要比Bellman-Ford演算法低,但適用範圍比Bellman-Ford演算法窄。 迪傑斯特拉提出的按路徑長度遞增次序來產生源點到各頂點的最短路徑的演算法思想是:對有n個頂點的有向連
【ACM】帶權有向圖單源最短路徑(Dijkstra演算法)
最短路徑的第一類問題 求從單個源點到其餘各頂點的最短路徑。這是一種貪心策略,不可以存在負權邊。 演算法簡介 給定帶權有向圖G和源點v0,求從源點v0到G中其餘各頂點的最短路徑。迪傑斯特拉演算法是對
Java資料結構----圖--最短路徑解法Dijkstra演算法和Floyd演算法
最短路徑—Dijkstra演算法和Floyd演算法 1、Dijkstra演算法 1.1、定義概覽 Dijkstra(迪傑斯特拉)演算法是典型的單源最短路徑演算法,用於計算一個節點到其他所有節點的最短路徑。主要特點是以起始點為中心向外層層擴充套件,直到擴充套件到終點為止。Di
【最短路徑】dijkstra演算法 pascal
dijkstra演算法適用於無負邊的圖 var f:array[1..100] of boolean; cost:array[1..100,1..100] of longint; f
最短路徑之Dijkstra演算法及例項分析
Dijkstra演算法迪科斯徹演算法 Dijkstra演算法描述為:假設用帶權鄰接矩陣來表示帶權有向圖。首先引進一個輔助向量D,它的每個分量D[i]表示當前所找到的從始點v到每個終點Vi的最短路徑。它的初始狀態為:若兩頂點之間有弧,則D[i]為弧上的權值;否則置D[i]為無
最短路徑的Dijkstra演算法(鄰接表)
描述 以鄰接表作為儲存結構實現,求解從給定源點到給定結束點的最短路徑。 輸入 從1開始表示第一個節點。 第一行輸入:頂點數n(2<=n<=100),邊數m(2<=m<=100) 第二行輸入有向邊:起始點s1,結束點 s2,邊權值 w 第三
最短路徑之Dijkstra演算法思想講解
1 最短路徑演算法 在日常生活中,我們如果需要常常往返A地區和B地區之間,我們最希望知道的可能是從A地區到B地區間的眾多路徑中,那一條路徑的路途最短。最短路徑問題是圖論研究中的一個經典演算法問題, 旨在尋找圖(由結點和路徑組成的)中兩結點之間的最短路徑。 演算法具體的
最短路徑的Dijkstra演算法
1 /* 2 * Copyright (c) 2013 eryar All Rights Reserved. 3 * 4 * File : Main.cpp 5 * Author : [email protected] 6 *
演算法筆記--最短路徑之dijkstra演算法
1 最短路徑演算法 在日常生活中,我們如果需要常常往返A地區和B地區之間