掃描線演算法適合對向量圖形進行區域填充，只需要直到多邊形區域的幾何位置，不需要指定種子點，適合計算機自動進行圖形處理的場合使用，比如電腦遊戲和三維CAD軟體的渲染等等。

        對向量多邊形區域填充，演算法核心還是求交。《計算幾何與圖形學有關的幾種常用演算法》一文給出了判斷點與多邊形關係的演算法――掃描交點的奇偶數判斷演算法，利用此演算法可以判斷一個點是否在多邊形內，也就是是否需要填充，但是實際工程中使用的填充演算法都是隻使用求交的思想，並不直接使用這種求交演算法。究其原因，除了演算法效率問題之外，還存在一個光柵圖形裝置和向量之間的轉換問題。比如某個點位於非常靠近邊界的臨界位置，用向量演算法判斷這個點應該是在多邊形內，但是光柵化後，這個點在光柵圖形裝置上看就有可能是在多邊形外邊（向量點沒有大小概念，光柵圖形裝置的點有大小概念），因此，適用於向量圖形的填充演算法必須適應光柵圖形裝置。

2.1掃描線演算法的基本思想

        掃描線填充演算法的基本思想是：用水平掃描線從上到下（或從下到上）掃描由多條首尾相連的線段構成的多邊形，每根掃描線與多邊形的某些邊產生一系列交點。將這些交點按照x座標排序，將排序後的點兩兩成對，作為線段的兩個端點，以所填的顏色畫水平直線。多邊形被掃描完畢後，顏色填充也就完成了。掃描線填充演算法也可以歸納為以下4個步驟：

（1）       求交，計算掃描線與多邊形的交點

（2）       交點排序，對第2步得到的交點按照x值從小到大進行排序；

（3）       顏色填充，對排序後的交點兩兩組成一個水平線段，以畫線段的方式進行顏色填充；

（4）       是否完成多邊形掃描？如果是就結束演算法，如果不是就改變掃描線，然後轉第1步繼續處理；

        整個演算法的關鍵是第1步，需要用盡量少的計算量求出交點，還要考慮交點是線段端點的特殊情況，最後，交點的步進計算最好是整數，便於光柵裝置輸出顯示。

        對於每一條掃描線，如果每次都按照正常的線段求交演算法進行計算，則計算量大，而且效率底下，如圖（6）所示：

圖（6） 多邊形與掃描線示意圖

觀察多邊形與掃描線的交點情況，可以得到以下兩個特點：

（1）       每次只有相關的幾條邊可能與掃描線有交點，不必對所有的邊進行求交計算；

（2）       相鄰的掃描線與同一直線段的交點存在步進關係，這個關係與直線段所在直線的斜率有關；

        第一個特點是顯而易見的，為了減少計算量，掃描線演算法需要維護一張由“活動邊”組成的表，稱為“活動邊表（AET）”。例如掃描線4的“活動邊表”由P1P2和P3P4兩條邊組成，而掃描線7的“活動邊表”由P1P2、P6P1、P5P6和P4P5四條邊組成。

        第二個特點可以進一步證明，假設當前掃描線與多邊形的某一條邊的交點已經通過直線段求交演算法計算出來，得到交點的座標為（x, y），則下一條掃描線與這條邊的交點不需要再求交計算，通過步進關係可以直接得到新交點座標為（x + △x, y + 1）。前面提到過，步進關係△x是個常量，與直線的斜率有關，下面就來推導這個△x。

        假設多邊形某條邊所在的直線方程是：ax + by + c = 0，掃描線y_i和下一條掃描線y_i+1與該邊的兩個交點分別是（x_i，y_i）和（x_i+1，y_i+1），則可得到以下兩個等式：

ax_i + by_i + c = 0                        (等式 1)

ax_i+1 + by_i+1 + c = 0                     (等式 2)

由等式1可以得到等式3：

x_i = -(by_i + c) / a                           (等式 3)

同樣，由等式2可以得到等式4：

x_i+1 = -(by_i+1 + c) / a                      (等式 4)

由等式 4 – 等式3可得到

x_i+1 – x_i = -b (y_i+1 - y_i) / a

由於掃描線存在y_i+1 = y_i + 1的關係，將代入上式即可得到：

x_i+1 – x_i = -b / a

即△x = -b / a，是個常量（直線斜率的倒數）。

        “活動邊表”是掃描線填充演算法的核心，整個演算法都是圍繞者這張表進行處理的。要完整的定義“活動邊表”，需要先定義邊的資料結構。每條邊都和掃描線有個交點，掃描線填充演算法只關注交點的x座標。每當處理下一條掃描線時，根據△x直接計算出新掃描線與邊的交點x座標，可以避免複雜的求交計算。一條邊不會一直待在“活動邊表”中，當掃描線與之沒有交點時，要將其從“活動邊表”中刪除，判斷是否有交點的依據就是看掃描線y是否大於這條邊兩個端點的y座標值，為此，需要記錄邊的y座標的最大值。根據以上分析，邊的資料結構可以定義如下：

 根據EDGE的定義，掃描線4和掃描線7的“活動邊表”就分別如圖（7）和圖(8)所示：

 圖（7） 掃描線4的活動邊表

 圖（8） 掃描線7的活動邊表

        前面提到過，掃描線演算法的核心就是圍繞“活動邊表（AET）”展開的，為了方便活性邊表的建立與更新，我們為每一條掃描線建立一個“新邊表（NET）”，存放該掃描線第一次出現的邊。當演算法處理到某條掃描線時，就將這條掃描線的“新邊表”中的所有邊逐一插入到“活動邊表”中。“新邊表”通常在演算法開始時建立，建立“新邊表”的規則就是：如果某條邊的較低端點（y座標較小的那個點）的y座標與掃描線y相等，則該邊就是掃描線y的新邊，應該加入掃描線y的“新邊表”。上例中各掃描線的“新邊表”如下圖所示：

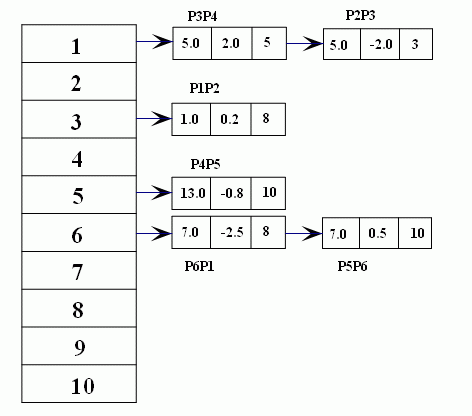
圖（9） 各掃描線的新邊表

        討論完“活動邊表（AET）”和“新邊表（NET）”，就可以開始演算法的具體實現了，但是在進一步詳細介紹實現演算法之前，還有以下幾個關鍵的細節問題需要明確：

（1）      多邊形頂點處理

        在對多邊形的邊進行求交的過程中，在兩條邊相連的頂點處會出現一些特殊情況，因為此時兩條邊會和掃描線各求的一個交點，也就是說，在頂點位置會出現兩個交點。當出現這種情況的時候，會對填充產生影響，因為填充的過程是成對選擇交點的過程，錯誤的計算交點個數，會造成填充異常。

        假設多邊形按照頂點P1、P2和P3的順序產生兩條相鄰的邊，P2就是所說的頂點。多邊形的頂點一般有四種情況，如圖（10）所展示的那樣，分別被稱為左頂點、右頂點、上頂點和下頂點：

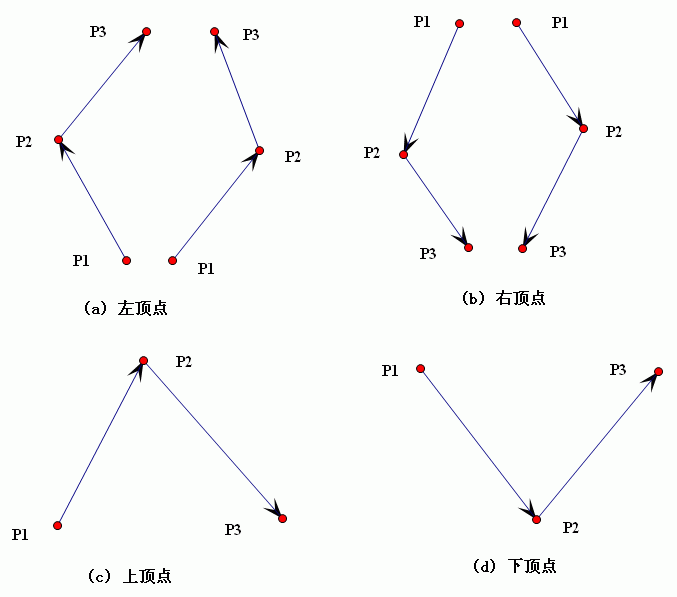
圖（10） 多邊形頂點的四種類型

左頂點――P1、P2和P3的y座標滿足條件 ：y1 < y2 < y3；

右頂點――P1、P2和P3的y座標滿足條件 ：y1 > y2 > y3；

上頂點――P1、P2和P3的y座標滿足條件 ：y2 > y1 && y2 > y3；

下頂點――P1、P2和P3的y座標滿足條件 ：y2 < y1 && y2 < y3；

        對於左頂點和右頂點的情況，如果不做特殊處理會導致奇偶奇數錯誤，常採用的修正方法是修改以頂點為終點的那條邊的區間，將頂點排除在區間之外，也就是刪除這條邊的終點，這樣在計算交點時，就可以少計算一個交點，平衡和交點奇偶個數。結合前文定義的“邊”資料結構：EDGE，只要將該邊的ymax修改為ymax – 1就可以了。

        對於上頂點和下頂點，一種處理方法是將交點計算做0個，也就是修正兩條邊的區間，將交點從兩條邊中排除；另一種處理方法是不做特殊處理，就計算2個交點，這樣也能保證交點奇偶個數平衡。

（2）      水平邊的處理

    水平邊與掃描線重合，會產生很多交點，通常的做法是將水平邊直接畫出（填充），然後在後面的處理中就忽略水平邊，不對其進行求交計算。

（3）      如何避免填充越過邊界線

        邊界畫素的取捨問題也需要特別注意。多邊形的邊界與掃描線會產生兩個交點，填充時如果對兩個交點以及之間的區域都填充，容易造成填充範圍擴大，影響最終光柵圖形化顯示的填充效果。為此，人們提出了“左閉右開”的原則，簡單解釋就是，如果掃描線交點是1和9，則實際填充的區間是[1,9），即不包括x座標是9的那個點。

2.2掃描線演算法實現

        掃描線演算法的整個過程都是圍繞“活動邊表（AET）”展開的，為了正確初始化“活動邊表”，需要初始化每條掃描線的“新邊表（NET）”，首先定義“新邊表”的資料結構。定義“新邊表”為一個數組，陣列的每個元素存放對應掃描線的所有“新邊”。因此定義“新邊表”如下：

ymax和ymin是多邊形所有頂點中y座標的最大值和最小值，用於界定掃描線的範圍。slNet 中的第一個元素對應的是ymin所在的掃描線，以此類推，最後一個元素是ymax所在的掃描線。在開始對每條掃描線處理之前，需要先計算出多邊形的ymax和ymin並初始化“新邊表”：

        InitScanLineNewEdgeTable()函式根據多邊形的頂點和邊的情況初始化“新邊表”，實現過程中體現了對左頂點和右頂點的區間修正原則：

多邊形的定義Polygon和本系列第一篇《計算幾何與圖形學有關的幾種常用演算法》一文中的定義一致，此處就不再重複說明。演算法通過遍歷所有的頂點獲得邊的資訊，然後根據與此邊有關的前後兩個頂點的情況確定此邊的ymax是否需要-1修正。ps和pe分別是當前處理邊的起點和終點，pss是起點的前一個相鄰點，pee是終點的後一個相鄰點，pss和pee用於輔助判斷ps和pe兩個點是否是左頂點或右頂點，然後根據判斷結果對此邊的ymax進行-1修正，演算法實現非常簡單，注意與掃描線平行的邊是不處理的，因為水平邊直接在HorizonEdgeFill()函式中填充了。

         ProcessScanLineFill()函式開始對每條掃描線進行處理，對每條掃描線的處理有四個操作，如下程式碼所示，四個操作分別被封裝到四個函式中：

InsertNetListToAet()函式負責將掃描線對應的所有新邊插入到aet中，插入操作到保證aet還是有序表，應用了插入排序的思想，實現簡單，此處不多解釋。FillAetScanLine()函式執行具體的填充動作，它將aet中的邊交點成對取出組成填充區間，然後根據“左閉右開”的原則對每個區間填充，實現也很簡單，此處不多解釋。RemoveNonActiveEdgeFromAet()函式負責將對下一條掃描線來說已經不是“活動邊”的邊從aet中刪除，刪除的條件就是當前掃描線y與邊的ymax相等，如果有多條邊滿足這個條件，則一併全部刪除：

UpdateAndResortAet()函式更新邊表中每項的xi值，就是根據掃描線的連貫性用dx對其進行修正，並且根據xi從小到大的原則對更新後的aet表重新排序：

        其實更新完xi後對aet表的重新排序是可以避免的，只要在維護aet時，除了保證xi從小到大的排序外，在xi相同的情況下如果能保證修正量dx也是從小到大有序，就可以避免每次對aet進行重新排序。演算法實現也很簡單，只需要對InsertNetListToAet()函式稍作修改即可，有興趣的朋友可以自行修改。

        至此，掃描線演算法就介紹完了，演算法的思想看似複雜，實際上並不難，從具體演算法的實現就可以看出來，整個演算法實現不足百行程式碼。

<下一篇：一種改進的掃描線演算法>