算法系列之十二:多邊形區域填充演算法--遞迴種子填充演算法
平面區域填充演算法是計算機圖形學領域的一個很重要的演算法,區域填充即給出一個區域的邊界(也可以是沒有邊界,只是給出指定顏色),要求將邊界範圍內的所有象素單元都修改成指定的顏色(也可能是圖案填充)。區域填充中最常用的是多邊形填色,本文中我們就討論幾種多邊形區域填充演算法。
一、種子填充演算法(Seed Filling)
如果要填充的區域是以影象元資料方式給出的,通常使用種子填充演算法(Seed Filling)進行區域填充。種子填充演算法需要給出影象資料的區域,以及區域內的一個點,這種演算法比較適合人機互動方式進行的影象填充操作,不適合計算機自動處理和判斷填色。根據對影象區域邊界定義方式以及對點的顏色修改方式,種子填充又可細分為幾類,比如注入填充演算法(Flood Fill Algorithm)、邊界填充演算法(Boundary Fill Algorithm)以及為減少遞迴和壓棧次數而改進的掃描線種子填充演算法等等。
所有種子填充演算法的核心其實就是一個遞迴演算法,都是從指定的種子點開始,向各個方向上搜索,逐個畫素進行處理,直到遇到邊界,各種種子填充演算法只是在處理顏色和邊界的方式上有所不同。在開始介紹種子填充演算法之前,首先也介紹兩個概念,就是“4-聯通演算法”和“8-聯通演算法”。既然是搜尋就涉及到搜尋的方向問題,從區域內任意一點出發,如果只是通過上、下、左、右四個方向搜尋到達區域內的任意畫素,則用這種方法填充的區域就稱為四連通域,這種填充方法就稱為“4-聯通演算法”。如果從區域內任意一點出發,通過上、下、左、右、左上、左下、右上和右下全部八個方向到達區域內的任意畫素,則這種方法填充的區域就稱為八連通域,這種填充方法就稱為“8-聯通演算法”。如圖1(a)所示,假設中心的藍色點是當前處理的點,如果是“4-聯通演算法”,則只搜尋處理周圍藍色標識的四個點,如果是“8-聯通演算法”則除了處理上、下、左、右四個藍色標識的點,還搜尋處理四個紅色標識的點。兩種搜尋演算法的填充效果分別如如圖1(b)和圖1(c)所示,假如都是從黃色點開始填充,則“4-聯通演算法”如圖1(b)所示只搜尋填充左下角的區域,而“8-聯通演算法”則如圖1(c)所示,將左下角和右上角的區域都填充了。
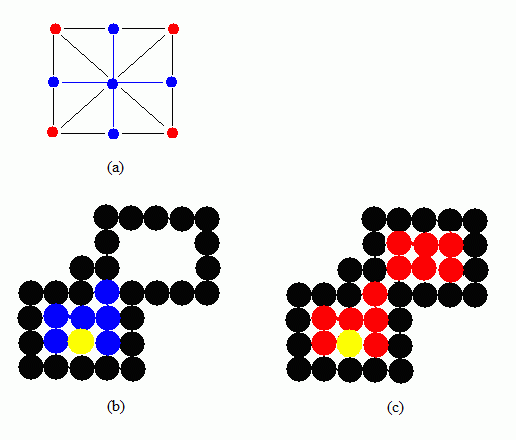
圖(1) “4-聯通”和“8-聯通”填充效果
並不能僅僅因為圖1的填充效果就認為“8-聯通演算法”一定比“4-聯通演算法”好,應該根據應用環境和實際的需求選擇聯通搜尋方式,在很多情況下,只有“4-聯通演算法”才能得到正確的結果。
1.1 注入填充演算法(Flood Fill Algorithm)
注入填充演算法不特別強調區域的邊界,它只是從指定位置開始,將所有聯通區域內某種指定顏色的點都替換成另一種顏色,從而實現填充效果。注入填充演算法能夠實現顏色替換之類的功能,這在影象處理軟體中都得到了廣泛的應用。注入填充演算法的實現非常簡單,核心就是遞迴和搜尋,以下就是注入填充演算法的一個實現:
164 void FloodSeedFill(int x, int y, int old_color, int new_color) 165 { 166 if(GetPixelColor(x, y) == old_color) 167 { 168 SetPixelColor(x, y, new_color); 169 for(int i = 0; i < COUNT_OF(direction_8); i++) 170 { 171 FloodSeedFill(x + direction_8[i].x_offset, 172 y + direction_8[i].y_offset, old_color, new_color); 173 } 174 } 175 } |
for迴圈實現了向8個聯通方向的遞迴搜尋,祕密就在direction_8的定義:
15 typedef struct tagDIRECTION 16 { 17 int x_offset; 18 int y_offset; 19 }DIRECTION; |
79 DIRECTION direction_8[] = { {-1, 0}, {-1, 1}, {0, 1}, {1, 1}, {1, 0}, {1, -1}, {0, -1}, {-1, -1} }; |
這個是搜尋類演算法中常用的技巧,無需做太多說明,其實只要將其替換成如下direction_4的定義,就可以將演算法改成4個聯通方向填充演算法:
80 DIRECTION direction_4[] = { {-1, 0}, {0, 1}, {1, 0}, {0, -1} }; |
圖2就是應用本演算法實現的“4-聯通”和“8-聯通”填充效果:

圖(2) 注入填充演算法實現
1.2 邊界填充演算法(Boundary Fill Algorithm)
邊界填充演算法與注入填充演算法的本質其實是一樣的,都是遞迴和搜尋,區別只在於對邊界的確認,也就是遞迴的結束條件不一樣。注入填充演算法沒有邊界的概念,只是對聯通區域內指定的顏色進行替換,而邊界填充演算法恰恰強調邊界的存在,只要是邊界內的點無論是什麼顏色,都替換成指定的顏色。邊界填充演算法在應用上也非常的廣泛,畫圖軟體中的“油漆桶”功能就是邊界填充演算法的例子。以下就是邊界填充演算法的一個實現:
177 void BoundarySeedFill(int x, int y, int new_color, int boundary_color) 178 { 179 int curColor = GetPixelColor(x, y); 180 if( (curColor != boundary_color) 181 && (curColor != new_color) ) 182 { 183 SetPixelColor(x, y, new_color); 184 for(int i = 0; i < COUNT_OF(direction_8); i++) 185 { 186 BoundarySeedFill(x + direction_8[i].x_offset, 187 y + direction_8[i].y_offset, new_color, boundary_color); 188 } 189 } 190 } |
關於direction_8的說明請參考上一節,圖3就是應用本演算法實現的“4-聯通”和“8-聯通”填充效果(其中顏色值是1的點就是指定的邊界):

圖(3) 邊界填充演算法實現
<下一篇:掃描線種子填充演算法>
