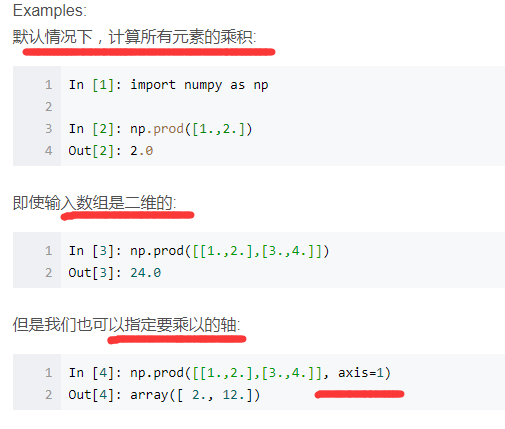
np.prod() 函式計算陣列元素乘積等
np.prod()函式用來計算所有元素的乘積,對於有多個維度的陣列可以指定軸,如axis=1指定計算每一行的乘積。
Python format 格式化函式:
例1: >>>"{} {}".format("hello", "world") # 不設定指定位置,按預設順序 'hello world' >>> "{0} {1}".format("hello", "world") # 設定指定位置 'hello world' >>> "{1} {0} {1}".format("hello", "world") # 設定指定位置 'world hello world' 例2: #!/usr/bin/python # -*- coding: UTF-8 -*- print("網站名:{name}, 地址 {url}".format(name="菜鳥教程", url="www.runoob.com")) # 通過字典設定引數 site = {"name": "菜鳥教程", "url": "www.runoob.com"} print("網站名:{name}, 地址 {url}".format(**site)) # 通過列表索引設定引數 my_list = ['菜鳥教程', 'www.runoob.com'] print("網站名:{0[0]}, 地址 {0[1]}".format(my_list)) # "0" 是必須的
python進階發現的資源,後續有實際應用另行更新:
KNN 分類器的K值選取:K值不能過大,也不能過小,K值的選取取決於學習難度與訓練樣本的規模,通常,K取3~10。一種常見的做法就是設定K等於訓練樣本數的“平方根”。更好的一種方法是“交叉驗證”:設定多個測試樣本集,用這些樣本集來測試多個K值,根據分類效能選擇最合適的K值。
從知乎上看到的資料清洗方面的知識:
資料探勘中常用的資料清洗方法有哪些?
python排序,保留索引值
: 比如對a = [3,4,1,7,2]用a.sort()排序得到a = [1,2,3,4,7],請問如何得到排序後的
: 陣列元素的索引系列,是說,在原來陣列中的索引。在這個例子裡應該是[2,4,0,1,3].
In [1]: a = [3,4,1,7,2]
In [2]: enumerate(a)
Out[2]: <enumerate object at 0x8591f0c>
In [3]: list(enumerate(a))
Out[3]: [(0, 3), (1, 4), (2, 1), (3, 7), (4, 2)]
In [4]: from operator import itemgetter
In [5]: sorted(enumerate(a), key=itemgetter(1))
Out[5]: [(2, 1), (4, 2), (0, 3), (1, 4), (3, 7)]
In [6]: [index for index, value in sorted(enumerate(a), key=itemgetter(1))]
Out[6]: [2, 4, 0, 1, 3]
大殺器:
In [7]: import numpy as np
In [8]: np.argsort([3,4,1,7,2])
Out[8]: array([2, 4, 0, 1, 3])
注意的是,對於 [(索引,值),...,(索引,值)]這種形式的情況我以為對任意的索引值都可以用,但其實不是,例如:
# 使用jupyter notebook a=[(12,4),(100,3),(1000,1),(9832,2)] from operator import itemgetter [index for index,value in sorted(enumerate(a),key=itemgetter(1))] Output[1]:[0, 1, 2, 3] # 注意,我是把12,100,1000,9832當做索引值的,即“任意索引值”,但是發現輸出的不是例子中給出的那樣,實際情況仍然是索引從0開始的情況。後來我是用for迴圈解決的: Input:a=sorted(a,key=itemgetter(1)) a Output:[(1000, 1), (9832, 2), (100, 3), (12, 4)] # a排序後的效果 #接著上面提取任意索引: Input: indx=[] a=a[:len(a)/2] for i in a: indx.append(i[0]) Output: indx [1000, 9832] # 提取出值最小的兩個值對應的索引。
其他關於python排序的高階技巧請自行搜尋
python面向物件:
現在面向物件的思維用的很多,大到實際生活工作中的問題或小/具體到程式設計問題,你要時時注意到你討論的問題的物件是什麼,是對什麼討論的這個問題。比如今天下午討論的影象聚類和影象劃分,一個面向的物件是一張張圖片,目的是把相似的圖片進行聚類;另一個問題的物件是圖片中的一個個畫素點的值,目的是對一張圖片的不同區域進行劃分。問題的物件就不一樣,要是一下子就能意識到問題的物件變了,就可以流暢的在不同的問題場景中轉換。
好了,扯遠了,,回來回來,說到python面向物件我本意是想說python面向物件中的類,類中屬性是可以直接通過類名進行訪問的,而類的方法如果沒有加“@classmethod”這樣的裝飾器的話需要先把類例項化一個具體的類的例項物件,即要通過一個類的實體才能去呼叫這個方法;對於有些方法不需要傳入引數的,可以用裝飾器“@property” 把這個方法裝飾成類的一個屬性,這樣就可以通過類名直接呼叫了,而且不用加方法的“()”,就像呼叫類的一般屬性的方式那樣呼叫就行了。
好,這部分今天就說到這裡~
python & tensorflow 設定學習率:
先設定一個learning_rate 例項,再傳入優化器Optimizer()中。
import tensorflow as tf
from numpy.random import RandomState
if __name__ == "__main__":
#設定每次跌打資料的大小
batch_size = 8
#定義輸入節點
x = tf.placeholder(tf.float32,shape=(None,1),name="x_input")
#定義預測值的輸出節點
y_ = tf.placeholder(tf.float32,shape=(None,1),name="y_output")
#定義引數變數
w = tf.Variable(50.,trainable=True)
# 定義神經網路的傳播過程
y = x * w
#定義損失函式
loss = tf.reduce_sum(tf.square(y-y_))
#定義global_step
global_step = tf.Variable(0,trainable=False)
#通過指數衰減函式來生成學習率
learing_rate = tf.train.exponential_decay(0.1,global_step,100,0.96,staircase=False)
#使用梯度下降演算法來最優化損失值
learing_step = tf.train.GradientDescentOptimizer(learing_rate).minimize(loss,global_step)
#隨機產生一個數據集
rdm = RandomState(1)
#設定資料集的大小
dataset_size = 200
#產生輸入資料
X = rdm.rand(dataset_size,1)
#定義真實的輸出資料Y,
Y = [x1 + rdm.rand()/5.0 - 0.05 for x1 in X]
#訓練模型
with tf.Session() as sess:
#初始化所有的引數
all_init = tf.initialize_all_variables()
sess.run(all_init)
#設定迭代次數
STEPS = 5000
for i in range(STEPS):
start = (i * batch_size) % batch_size
end = min(start+batch_size,dataset_size)
#訓練模型
sess.run(fetches=learing_step,feed_dict={x:X[start:end],y_:Y[start:end]})
#沒迭代100次輸出一次引數值
if i % 100 == 0:
print("w:%f,learing_rate:%f"%(w.eval(session=sess),learing_rate.eval(session=sess)))
深度學習中的“batch_size”引數:
如果資料集比較小,則可以採用全資料集(即‘Full Batch Learing’),但是對於更大的資料集並不適用。相對於Full Batch Learning的另一個極端就是一個batch只有一個數據,叫“線上學習(Online Learning)”, 線性神經元在均方誤差代價函式的錯誤面是一個拋物面,橫截面是橢圓。對於多層神經元、非線性網路,在區域性依然是近似拋物面。使用線上學習(online learning)每次修正的方向以各自樣本的梯度方向修正,橫衝直撞,難以達到收斂。
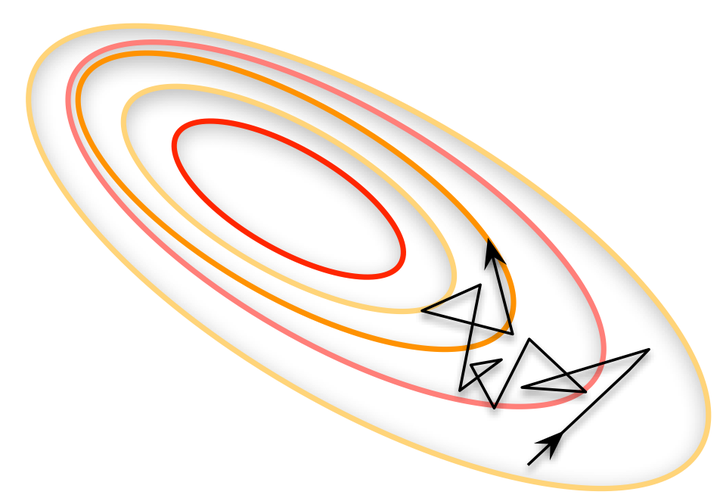
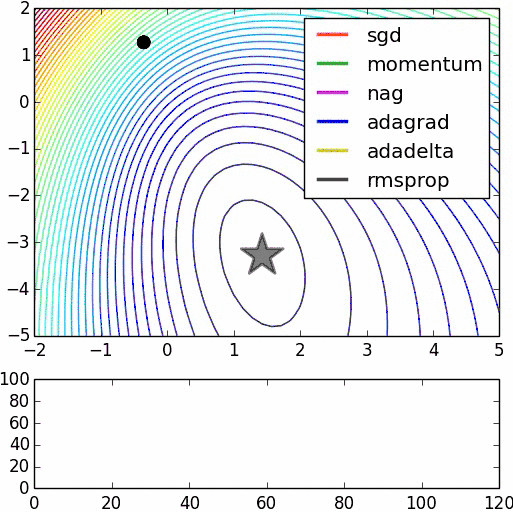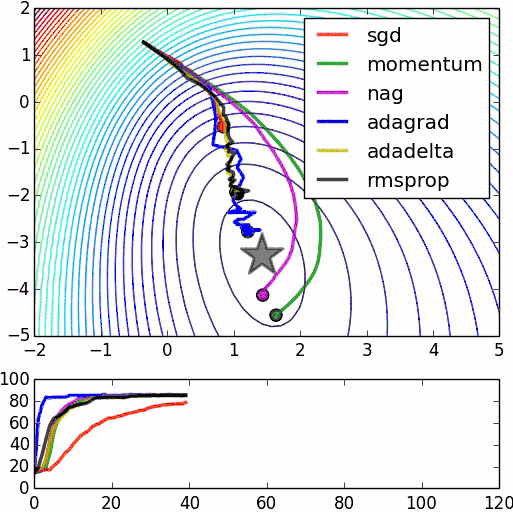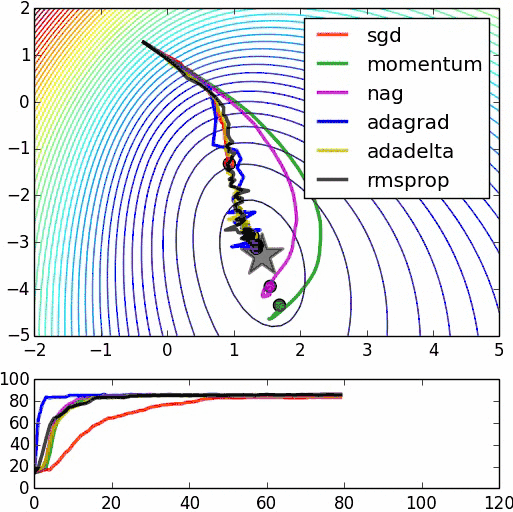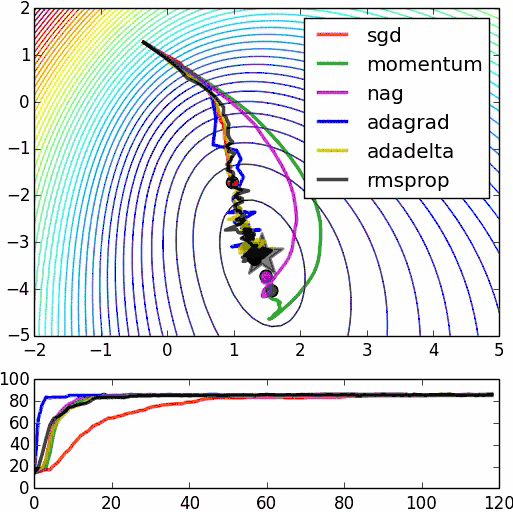 不同隨機優化器的比較:
不同隨機優化器的比較: