因為本人是自學深度學習的，有什麼說的不對的地方望大神指出

指數加權平均演算法的原理

TensorFlow中的滑動平均模型使用的是滑動平均（Moving Average）演算法，又稱為指數加權移動平均演算法（exponenentially weighted average），這也是ExponentialMovingAverage()函式的名稱由來。
先來看一個簡單的例子，這個例子來自吳恩達老師的DeepLearning課程，個人強烈推薦初學者都看一下。
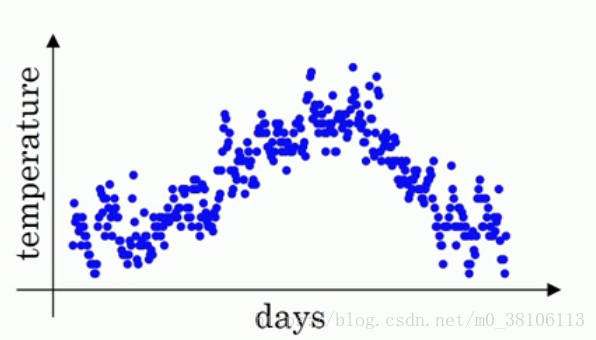
開始例子。首先這是一年365天的溫度散點圖，以天數為橫座標，溫度為縱座標，你可以看見各個小點分佈在圖上，有一定的曲線趨勢，但是並不明顯

接著，如果我們要看出這個溫度的變化趨勢，很明顯需要做一點處理，也即是我們的主題，用滑動平均演算法處理。
首先給定一個值v0，然後我們定義每一天的溫度是a1，a2，a3·····
接著，我們計算出v1，v2，v3····來代替每一天的溫度，也就是上面的a1，a2，a3
計算方法是：v1 = v0 * 0.9 + a1 （1-0.9），v2= v1 0.9 + a2 （1-0.9），v3= v2 0.9 + a3 （1-0.9）···，也就是說，每一天的溫度改變為前一天的v值 0.9 + 當天的溫度 * 0.1，vt = v(t-1) * 0.9 + at * 0.1，把所有的v計算完之後畫圖，紅線就是v的曲線：

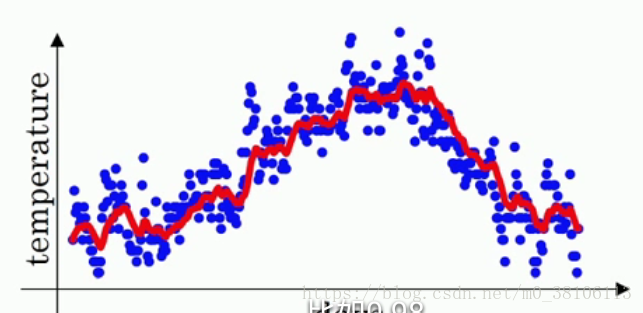
v值就是指數加權平均數，整個過程就是指數加權平均演算法，它很好的把一年的溫度曲線給擬合了出來。把0.9抽象為β，總結為vt = v(t-1) * β + at * (1-β)。

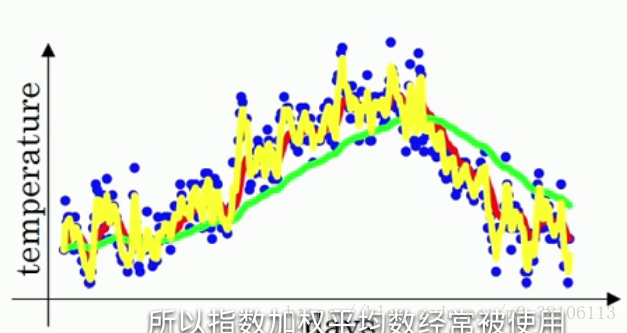
β這個值的意義是什麼？實際上vt ≈ 1/(1 - β) 天的平均溫度，例如：假設β等於0.9，1/(1 - β) 就等於10，也就是vt等於前十天的平均溫度，這個說可能不太看得出來；假設把β值調大道接近1，例如，將β等於0.98，1/(1-β)=50，按照剛剛的說法也就是前50天的平均溫度，然後求出v值畫出曲線，如圖所示：

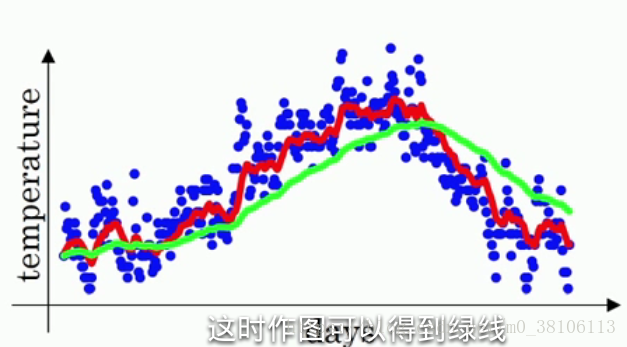
綠線就是β等於0.98時候的曲線，可以明顯看到綠線比紅線的變化更遲，紅線達到某一溫度，綠線要過一陣子才能達到相同溫度。因為綠線是前50天的平均溫度，變化就會更加緩慢，而紅線是最近十天的平均溫度，只要最近十天的溫度都是上升，紅線很快就能跟著變化。所以直觀的理解就是，vt是前1/(1-β)天的平均溫度。
再看看另一個極端情況：β等於0.5，意味著vt≈最近兩天的平均溫度，曲線如下黃線：

和原本的溫度很相似，但曲線的波動幅度也相當大！

然後說一下這個滑動平均模型和深度學習有什麼關係：通常來說，我們的資料也會像上面的溫度一樣，具有不同的值，如果使用滑動平均模型，就可以使得整體資料變得更加平滑——這意味著資料的噪音會更少，而且不會出現異常值。但是同時β太大也會使得資料的曲線右移，和資料不擬合。需要不斷嘗試出一個β值，既可以擬合數據集，又可以減少噪音。
滑動平均模型在深度學習中還有另一個優點：它只佔用極少的記憶體
當你在模型中計算最近十天（有些情況下遠大於十天）的平均值的時候，你需要在記憶體中載入這十天的資料然後進行計算，但是指數加權平均值約等於最近十天的平均值，而且根據vt = v(t-1) * β + at * (1-β)，你只需要提供at這一天的資料，再加上v(t-1)的值和β值，相比起十天的資料這是相當小的資料量，同時佔用更少的記憶體。

偏差修正

指數加權平均值通常都需要偏差修正，TensorFlow中提供的ExponentialMovingAverage()函式也帶有偏差修正。

首先看一下為什麼會出現偏差，再來說怎麼修正。當β等於0.98的時候，還是用回上面的溫度例子，曲線實際上不是像綠線一樣，而是像紫線：

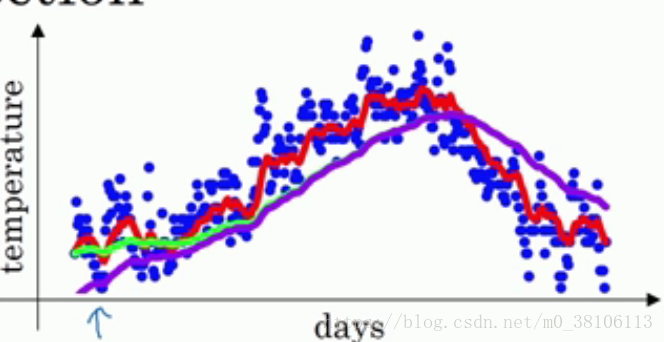
你可以注意到在紫線剛剛開始的時候，曲線的值相當的低，這是因為在一開始的時候並沒有50天（1/(1-β)為50）的資料，而是隻有寥寥幾天的資料，相當於少加了幾十天的資料，所以vt的值很小，這和實際情況的差距是很大的，也就是出現的偏差。
而在TensorFlow中的ExponentialMovingAverage()採取的偏差修正方法是：使用num_updates來動態設定β的大小

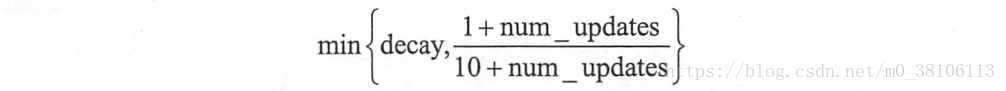
在資料迭代的前期，資料量比較少的時候，(1+num_updates)/(10+num_updates)的值比較小，使用這個值作為β來進行vt的計算，所以在迭代前期就會像上面的紅線一樣，和原資料更加接近。舉個例子，當天數是第五天，β為0.98，那麼(1+num_updates)/(10+num_updates) = 6/15 = 0.4，相當於最近1.6天的平均溫度，而不是β=0.98時候的50天，這樣子就做到了偏差修正。

滑動平均模型的程式碼實現

看到這裡你應該大概瞭解了滑動平均模型和偏差修正到底是怎麼回事了，接下來把這個想法對應到TensorFlow的程式碼中。

首先明確一點，TensorFlow中的ExponentialMovingAverage()是針對權重weight和偏差bias的，而不是針對訓練集的。如果你現在訓練集中實現這個效果，需要自己設計程式碼。
為什麼要對w和b使用滑動平均模型呢？因為在神經網路中，
更新的引數時候不能太大也不能太小，更新的引數跟你之前的引數有聯絡，不能發生突變。一旦訓練的時候遇到個“瘋狂”的引數，有了滑動平均模型，瘋狂的引數就會被抑制下來，回到正常的隊伍裡。這種對於突變引數的抑制作用，用專業術語講叫魯棒性，魯棒性就是對突變的抵抗能力，魯棒性越好，這個模型對惡性引數的提抗能力就越強。
在TensorFlow中，ExponentialMovingAverage()可以傳入兩個引數：衰減率（decay）和資料的迭代次數（step），這裡的decay和step分別對應我們的β和num_updates，所以在實現滑動平均模型的時候，步驟如下：
1、定義訓練輪數step
2、然後定義滑動平均的類
3、給這個類指定需要用到滑動平均模型的變數（w和b）
4、執行操作，把變數變為指數加權平均值

    # 1、定義訓練的輪數，需要用trainable=False引數指定不訓練這個變數，
    # 避免這個變數被計算滑動平均值
    global_step = tf.Variable(0, trainable=False)

    # 2、給定滑動衰減率和訓練輪數，初始化滑動平均類
    # 定訓練輪數的變數可以加快訓練前期的迭代速度
    variable_averages = tf.train.ExponentialMovingAverage(MOVING_AVERAGE_DECAY,
                                                          global_step)
    # 3、用tf.trainable_variable()獲取所有可以訓練的變數列表，也就是所有的w和b
    # 全部指定為使用滑動平均模型
    variables_averages_op = variable_averages.apply(tf.trainable_variables())

    # 反向傳播更新引數之後，再更新每一個引數的滑動平均值，用下面的程式碼可以一次完成這兩個操作
    with tf.control_dependencies([train_step, variables_averages_op]):
        train_op = tf.no_op(name="train")

設定完使用滑動平均模型之後，只需要在每次使用反向傳播的時候改為使用run.(train_op)就可以正常執行了。