在採用隨機梯度下降（SGD）演算法訓練神經網路時，使用滑動平均模型可以一定程度增強引數的穩定性，提高最終模型在測試資料上的表現，使模型在測試資料上更健壯。

在TensorFlow中提供了tf.train.ExponentialMovingAverage(decay, steps)來實現滑動平均模型。ExponentialMovingAverage對每一個變數會維護一個影子變數，並且儲存在ExponentialMovingAverage.average(variable)，這個影子變數的初始值就是相應變數的初始值，而多次執行變數跟新時，影子變數的值會更新為：
影子變數=衰減率x影子變數+（1-衰減率）x待更新的變數

從公式中可以看到，衰減率決定了模型更新的速度，衰減率越大模型就越趨於穩定。在實際應用中，衰減率一般會設成非常接近1的數（比如0.999或0.9999）。為了使得模型在訓練前期可以更新的更快，ExponentialMovingAverage還提供了num_updates引數來動態設定decay的大小。如果在ExponentialMovingAverage初始化時提供了num_updates引數，那麼每次使用的衰減率將是：
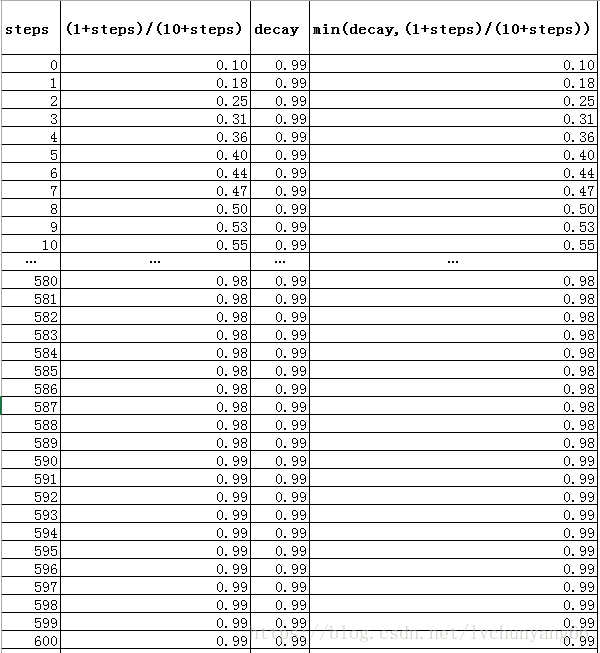
decay= min(decay,(1+steps)/(10+steps))
其中這裡的steps等於ExponentialMovingAverage中的引數num_updates，函式會內部自動計算min(decay,(1+steps)/(10+steps))從而確定decay的值。decay變化如下圖：

確定好ExponentialMovingAverage中的引數後，通過ExponentialMovingAverage(decay,num_updatas).apply([v1])來對變數v1進行滑動平均的操作。
下面是用python演示的一個案例：

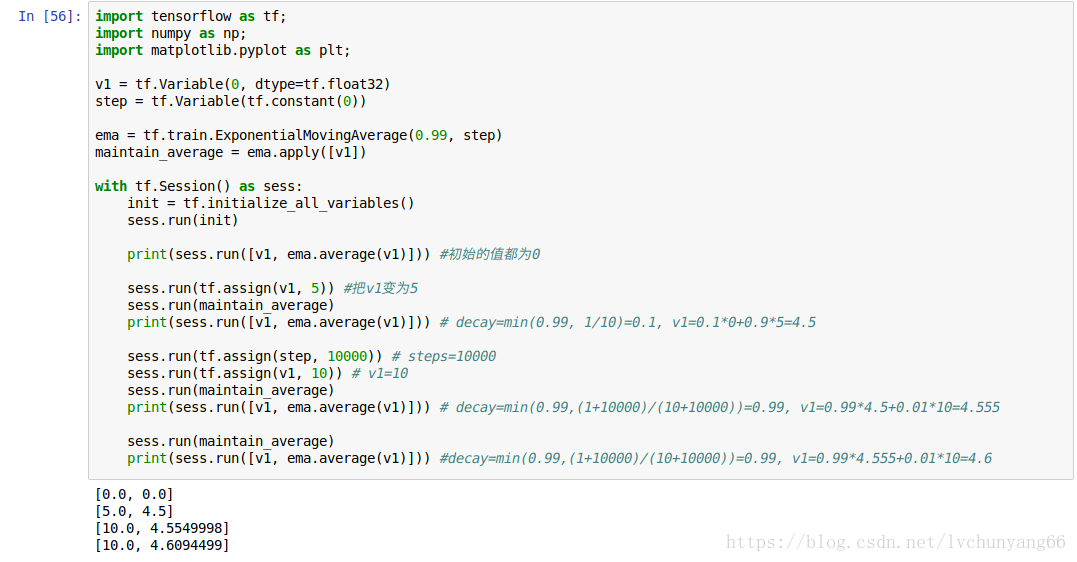
每次更新為以後，影子變數(ema.average(v1))的值會更新，待更新的變數為你設定的值。如果在下一次執行這個函式的時候你不再指定新的變數值，那麼待更新的變數值不變，影子變數會更新，如果待更新的變數值改變，影子變數也改變。

在梯度下降優化的幾個演算法裡，滑動加權平均的思想體現在動量梯度下降法（Gradient descent with Momentum）中。