線段樹學習(3)離散化 POJ 2528
阿新 • • 發佈:2019-01-22
看了好多關於線段樹離散化的資料,對離散化還是很陌生,於是嘗試著做一道需要離散化的線段樹題,來找一找感覺。資料上的離散化的知識,用不到題中(我好笨。。。),於是在網上找到了這題的程式碼,經過一番研究後,頓悟。
POJ 2528 對於初學者來說,是道不錯的題。
-----------------------------------------題目----------------------------------------------------------
They have built a wall 10000000 bytes long (such that there is enough place for all candidates). When the electoral campaign was restarted, the candidates were placing their posters on the wall and their posters differed widely in width. Moreover, the candidates started placing their posters on wall segments already occupied by other posters. Everyone in Bytetown was curious whose posters will be visible (entirely or in part) on the last day before elections.
Your task is to find the number of visible posters when all the posters are placed given the information about posters' size, their place and order of placement on the electoral wall.
The picture below illustrates the case of the sample input.
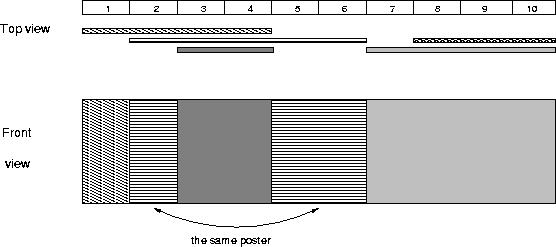
離散化的目的就是要將線段的長度適當的縮小,但不破壞題意。
比如:
------ (1,6)
------------ (1,12 )
像這樣這樣的兩條線段,可以把它們看作:
-- (1,2)
--- ( 1,3 )
這樣,縮短了線段的長度,但是他們的覆蓋關係並沒有改變。
關鍵我們要重新給壓縮後的線段標記起點和終點。
按照通用的離散化方法。。。。
首先依次讀入線段端點座標,存於post[MAXN][2]中,post[i][0]存第一條線段的起點,post[i][1]存第一條線段的終點,然後用一個結構題陣列line[MAXN]記錄資訊,line[i].li記錄端點座標,line[i].num記錄這個點屬於哪條線段(可以用正負數表示,負數表示起點,正數表示終點)。假如有N條線段,就有2*N個端點。然後將line陣列排序,按照端點的座標,從小到大排。接著要把線段賦予新的端點座標了。從左到右按照遞增的次序,依次更新端點,假如2*N個點中,共有M個不同座標的點,那麼線段樹的範圍就是[1,M]。
----------------------------------------------code------------------------------------------------------------
POJ 2528 對於初學者來說,是道不錯的題。
-----------------------------------------題目----------------------------------------------------------
Description
The citizens of Bytetown, AB, could not stand that the candidates in the mayoral election campaign have been placing their electoral posters at all places at their whim. The city council has finally decided to build an electoral wall for placing the posters and introduce the following rules:- Every candidate can place exactly one poster on the wall.
- All posters are of the same height equal to the height of
the wall; the width of a poster can be any integer number of bytes
(byte is the unit of length in Bytetown).
- The wall is divided into segments and the width of each segment is one byte.
- Each poster must completely cover a contiguous number of wall segments.
They have built a wall 10000000 bytes long (such that there is enough place for all candidates). When the electoral campaign was restarted, the candidates were placing their posters on the wall and their posters differed widely in width. Moreover, the candidates started placing their posters on wall segments already occupied by other posters. Everyone in Bytetown was curious whose posters will be visible (entirely or in part) on the last day before elections.
Your task is to find the number of visible posters when all the posters are placed given the information about posters' size, their place and order of placement on the electoral wall.
Input
Output
For each input data set print the number of visible posters after all the posters are placed.The picture below illustrates the case of the sample input.

Sample Input
1
5
1 4
2 6
8 10
3 4
7 10
Sample Output
4假如不離散化,那線段樹的上界是10e7,假如建一個那麼大的線段樹的話。。。必然MLE。於是要考慮離散化。
離散化的目的就是要將線段的長度適當的縮小,但不破壞題意。
比如:
------ (1,6)
------------ (1,12 )
像這樣這樣的兩條線段,可以把它們看作:
-- (1,2)
--- ( 1,3 )
這樣,縮短了線段的長度,但是他們的覆蓋關係並沒有改變。
關鍵我們要重新給壓縮後的線段標記起點和終點。
按照通用的離散化方法。。。。
首先依次讀入線段端點座標,存於post[MAXN][2]中,post[i][0]存第一條線段的起點,post[i][1]存第一條線段的終點,然後用一個結構題陣列line[MAXN]記錄資訊,line[i].li記錄端點座標,line[i].num記錄這個點屬於哪條線段(可以用正負數表示,負數表示起點,正數表示終點)。假如有N條線段,就有2*N個端點。然後將line陣列排序,按照端點的座標,從小到大排。接著要把線段賦予新的端點座標了。從左到右按照遞增的次序,依次更新端點,假如2*N個點中,共有M個不同座標的點,那麼線段樹的範圍就是[1,M]。
----------------------------------------------code------------------------------------------------------------
- #include<iostream>
- #include<algorithm>
- usingnamespace std;
- constint MAXN = 30000 ;
- struct NODE
- {
- int l,r,c;
- }tree[MAXN*5];
- struct L
- {
- int li,num;
- bool operator < ( const L& r ) const
- {
- return li<r.li;
- };
- };
- L line[MAXN];
- int post[MAXN][2];
- bool vis[MAXN];
- int cnt;
- void build ( int v , int l, int r )
- {
- int m;
- tree[v].c=0,tree[v].l=l,tree[v].r=r;
- if ( l>=r )
- return;
- m=(l+r)/2;
- build( v*2, l,m );
- build(v*2+1,m+1,r);
- }
- void ins (int v , int l , int r , int c )
- {
- int m;
- if ( tree[v].l==l && tree[v].r==r )
- {
- tree[v].c=c;
- return;
- }
- if ( tree[v].c>0 && tree[v].c!=c )
- {
- tree[v*2].c=tree[v].c;
- tree[v*2+1].c=tree[v].c;
- tree[v].c=0;
- }
- m=(tree[v].l+tree[v].r)>>1;
- if ( r<=m )
- ins(v*2,l,r,c);
- else
- if ( l>m )
- ins( v*2+1,l,r,c);
- else
- {
- ins(v*2,l,m,c);
- ins(v*2+1,m+1,r,c);
- }
- }
- void sum ( int v )
- {
- if ( tree[v].c )
- {
- if ( !vis[tree[v].c] )
- {
- vis[tree[v].c]=true;
- cnt++;
- }
- return;
- }
- sum(v*2);
- sum(v*2+1);
- }
- int main ( )
- {
- int n,N,i;
- scanf("%d",&N);
- while ( N-- )
- {
- cnt=0;
- scanf("%d",&n);
- memset(vis,false,sizeof(vis));
- //記錄端點
- for ( i=0 ; i<n ; i++ )
- {
- scanf("%d%d",&post[i][0],&post[i][1]);
- line[i*2].li=post[i][0],line[i*2].num=-(i+1),line[i*2+1].li=post[i][1],line[i*2+1].num=i+1;
- }
- //離散化座標
- sort(line,line+n*2);
- int tp=1,temp=line[0].li;
- for(i=0;i<2*n;i++)
- {
- if(line[i].li!=temp)
- {
- tp++;
- temp=line[i].li;
- }
- if(line[i].num<0)
- post[-line[i].num-1][0]=tp;
- else
- post[line[i].num-1][1]=tp;
- }
- build(1,1,tp);
- for ( i=0 ; i<n ; i++ )
- ins(1,post[i][0],post[i][1],i+1);
- sum(1);
- printf("%d/n",cnt);
- }
- }
