c# 四則混合運算演算法
阿新 • • 發佈:2019-01-22
對於四則混合運算其實在大三的時候就接觸過,但是由於當時自己太菜,只顧著玩遊戲跳課了。所以這個演算法一直沒有用程式碼實現過。當時學霸還給我簡單的講了一下方法,只因身為學渣的我,只想對學霸說一句,道理我都懂,但是用程式碼怎麼實現的呢。
這次寫這個實現四則混合運算功能的原因是,在專案中看到大牛寫了一個關於這個的功能,但是他用的是遍歷二叉樹和遞迴的原理,並且這段程式碼是在一個比較大的專案中層次結構比較複雜,實話說,我看得是似懂非懂,所以想自己實現一下,在下面可以提一下我對大牛寫的程式碼的原理的理解,可能不是很對。
今天說的也是利用了二叉樹遍歷的知識,不過沒有對二叉樹進行操作,只是利用了二叉樹的中序與後序遍歷的知識。下面將講解一下四則混合運算的原理,然後上部分程式碼。
一 . 原理
1. 中序表示式和後序表示式
例如表示式(A+B)*C+E/D,我們試圖將它分解,放到一個二叉樹中,那麼怎麼放到一個二叉樹中的,我們可以將這個表示式中的元素拆解成三個部分:
(A+B),C,E/D
我們發現A+B是二叉樹A+B中序遍歷的結果。令A+B的結果是F,則F*C是F*C中序遍歷的結果,依次類推,可以得出二叉樹如下:
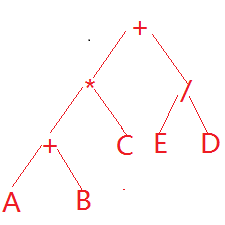
我們將這個二叉樹進行中序遍歷得到的就是如上的表示式。那麼為什麼要說這個呢。我們光看這個二叉樹中序遍歷的結果,對這個表示式進行詞法分析,是得不出什麼演算法的。但是我們可以對這個二叉樹的後序遍歷得到的表示式進行詞法分析的。
這個二叉樹後序遍歷的結果是:AB+C*ED/+
通過對後序表示式的詞法分析,我們令F=A+B,G=F*C,H=E/D,I=G*H,這樣我們就可以得到一個解決方法:每次遇到一個操作符,就將操作符的前兩個運算元與該操作符進行計算。
現在大概的思路有了,那麼中間需要解決的核心問題有如何將中序表示式轉換成後序表示式?如何對後序表示式進行計算?那麼且往下看。
2. 運算子優先順序
首先要說明的是這裡的優先順序不是四則運算中優先順序那麼簡單。我先列出一張優先順序表,然後再說明情況:
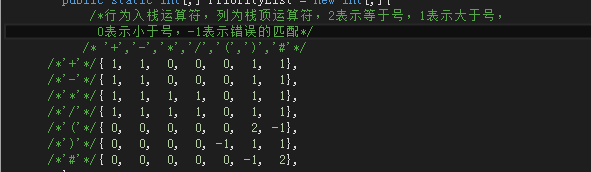
這個表顯示的是棧外的運算子與棧內運算子之間對比的優先順序表。
我們可以將上面的表示式入隊,然後進行壓棧和出棧操作,來得出後序表示式。在表示式後面加一個“#”運算子,那麼表示式就是(A+B)*C+E/D#,入隊後就是#D/E+C*)B+A(,“#”為隊尾元素,”(“為隊頭元素。設定一個棧,棧頂元素為”#”。
轉化規則:將佇列中的元素進行遍歷,如果是操作符則直接出隊,遇到操作符的時候要與棧頂進行比較,如果優先順序大於棧頂元素則該操作符出隊,如果小於棧頂元素,則棧頂元素出棧,該元素入棧,成為新的棧頂,這樣直到遍歷結束,最後得到的結果就是後序表示式。這裡如果優先順序相等則直接將棧頂元素出棧,該元素也出隊,並且不加入到後序表示式中。
這裡用了

可以參照優先順序看懂上面的圖的就說明你理解了實現原理。這就是著名的逆波蘭表示式。
3. 程式碼
//判斷是否為操作符
public bool isOperateors(string input)
{
if (input == "+" || input == "-" || input == "*" || input == "/"|| input == "(" || input == ")" || input == "#")
{
return true;
}
else return false;
}
/// <summary>
/// 分割表示式,併入佇列
/// </summary>
/// <param name="express"></param>
/// <returns>Queue</returns>
public Queue<string> SplitExpress(string express)
{
express += "#";
Queue<string> q = new Queue<string>();
string tempNum=string.Empty;
char[] arryExpress = express.ToArray<char>();
int i = 0;
int j = 0;
while (j<express.Length)
{
if (isOperateors(arryExpress[j].ToString()))
{
if (i != j)
{
tempNum = express.Substring(i, j - i);
q.Enqueue(tempNum);
q.Enqueue(arryExpress[j].ToString());
i = j + 1;
}
else
{
q.Enqueue(arryExpress[j].ToString());
i++;
}
}
j++;
}
//q.Enqueue("#");
return q;
}
/// <summary>
/// 中序表示式轉換為後序表示式
/// </summary>
/// <param name="q"></param>
/// <returns>string:後序表示式</returns>
public List<string> InorderToPostorder(Queue<string> q)
{
List<string> posterOrder = new List<string>();
Stack<string> inOrder = new Stack<string>();
inOrder.Push("#");
int count = q.Count;
for (int i = 0; i < count;i++ )
{
string item = q.Dequeue();
if (isOperateors(item))
{
string m = inOrder.First();
int n = Priority.isPriority(Priority.dicOperators[inOrder.First()],
Priority.dicOperators[item]);
while (n == 1)
{
string temp = inOrder.Pop();
if (temp != "(" && temp != ")")
{
posterOrder.Add(temp);
}
n = Priority.isPriority(Priority.dicOperators[inOrder.First()],
Priority.dicOperators[item]);
}
if (n == 2)
{
inOrder.Pop();
}
else if (n != -1)
{
inOrder.Push(item);
}
else
{
return null;
}
}
else
{
posterOrder.Add(item);
}
}
return inOrder.Count == 0 ? posterOrder : null;
}
/// <summary>
/// 計算後序表示式
/// </summary>
/// <param name="PostorderExpress"></param>
/// <param name="result"></param>
/// <returns></returns>
public bool IsResult(List<string> PostorderExpress, out decimal result)
{
if (PostorderExpress != null)
{
try
{
PostorderExpress.Add("#");
string[] tempArry = PostorderExpress.ToArray();
int length = tempArry.Length;
int i = 0;
while (tempArry[i] != "#")
{
if (isOperateors(tempArry[i]))
{
tempArry[i - 2] = Arithmetic(tempArry[i - 2], tempArry[i - 1], tempArry[i]);
for (int j = i; j < length; j++)
{
if (j + 1 < length)
tempArry[j - 1] = tempArry[j + 1];
}
length -= 2;
i -= 2;
}
i++;
}
result = decimal.Parse(tempArry[0]);
return true;
}
catch (Exception e)
{
result = 0;
return false;
}
}
else
{
result = 0;
return false;
}
}
//計算方法
public string Arithmetic(string x,string y,string operators)
{
decimal a = decimal.Parse(x);
decimal b = decimal.Parse(y);
decimal result = 0;
switch (operators)
{
case "+":
result = a + b;
break;
case "-":
result = a - b;
break;
case "*":
result = a * b;
break;
case "/":
result = a / b;
break;
}
return result.ToString();
}
下面給出原始碼下載連結:
http://download.csdn.net/detail/u012058778/9350639
說明:原始碼是本人用多半天時間純手寫的,如果各位測試的時候出現bug可以在回覆中說明一下,或者程式碼有不妥的地方都可以回覆一下,博主一定虛心接受。請不吝賜教。
然後上面說到大牛使用的方法,我是這樣理解的,他可能是遞迴生成二叉樹,然後對二叉樹進行計算(這裡的二叉樹只有三個結點),將計算的結果在與後面的表示式進行遞迴生成二叉樹,然後計算,直到得出結果。具體實現方法還有待研究,不過我覺得上面的壓棧方法效率會高些。
