十種常見的排序演算法
1.常見演算法分類
十種常見排序演算法一般分為以下幾種:
(1)非線性時間比較類排序:交換類排序(快速排序和氣泡排序)、插入類排序(簡單插入排序和希爾排序)、選擇類排序(簡單選擇排序和堆排序)、歸併排序(二路歸併排序和多路歸併排序);
(2)線性時間非比較類排序:計數排序、基數排序和桶排序。
總結:
(1)在比較類排序中,歸併排序號稱最快,其次是快速排序和堆排序,兩者不相伯仲,但是有一點需要注意,資料初始排序狀態對堆排序不會產生太大的影響,而快速排序卻恰恰相反。
(2)線性時間非比較類排序一般要優於非線性時間比較類排序,但前者對待排序元素的要求較為嚴格,比如計數排序要求待排序數的最大值不能太大,桶排序要求元素按照hash分桶後桶內元素的數量要均勻。線性時間非比較類排序的典型特點是以空間換時間。
注:本博文的示例程式碼均已遞增排序為目的。
2.演算法描述與實現
2.1交換類排序
交換排序的基本方法是:兩兩比較待排序記錄的排序碼,交換不滿足順序要求的偶對,直到全部滿足位置。常見的氣泡排序和快速排序就屬於交換類排序。
2.1.1氣泡排序
演算法思想:
從陣列中第一個數開始,依次遍歷陣列中的每一個數,通過相鄰比較交換,每一輪迴圈下來找出剩餘未排序數的中的最大數並”冒泡”至數列的頂端。
演算法步驟:
(1)從陣列中第一個數開始,依次與下一個數比較並次交換比自己小的數,直到最後一個數。如果發生交換,則繼續下面的步驟,如果未發生交換,則陣列有序,排序結束,此時時間複雜度為O(n);
(2)每一輪”冒泡”結束後,最大的數將出現在亂序數列的最後一位。重複步驟(1)。
穩定性:穩定排序。
時間複雜度: O(n)至O(n2)(function () {。
最好的情況:如果待排序資料序列為正序,則一趟冒泡就可完成排序,排序碼的比較次數為n-1次,且沒有移動,時間複雜度為O(n)。
最壞的情況:如果待排序資料序列為逆序,則氣泡排序需要n-1次趟起泡,每趟進行n-i次排序碼的比較和移動,即比較和移動次數均達到最大值:
比較次數:Cmax=∑i=1n−1(n−i)=n(n−1)/2=O(n2)
移動次數等於比較次數,因此最壞時間複雜度為O(n2)。
示例程式碼:
void bubbleSort(int array[],int len){
//迴圈的次數為陣列長度減一,剩下的一個數不需要排序
for(int i=0;i<len-1;++i){
bool noswap=true;
//迴圈次數為待排序數第一位數冒泡至最高位的比較次數
for(int j=0;j<len-i-1;++j){
if(array[j]>array[j+1]){
array[j]=array[j]+array[j+1];
array[j+1]=array[j]-array[j+1];
array[j]=array[j]-array[j+1];
//交換或者使用如下方式
//a=a^b;
//b=b^a;
//a=a^b;
noswap=false;
}
}
if(noswap) break;
}
}- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20

- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
2.1.2快速排序
氣泡排序是在相鄰的兩個記錄進行比較和交換,每次交換隻能上移或下移一個位置,導致總的比較與移動次數較多。快速排序又稱分割槽交換排序,是對氣泡排序的改進,快速排序採用的思想是分治思想。。
演算法原理:
(1)從待排序的n個記錄中任意選取一個記錄(通常選取第一個記錄)為分割槽標準;
(2)把所有小於該排序列的記錄移動到左邊,把所有大於該排序碼的記錄移動到右邊,中間放所選記錄,稱之為第一趟排序;
(3)然後對前後兩個子序列分別重複上述過程,直到所有記錄都排好序。
穩定性:不穩定排序。
時間複雜度: O(nlog2n)。
最好的情況:是每趟排序結束後,每次劃分使兩個子檔案的長度大致相等,時間複雜度為O(nlog2n)。
最壞的情況:是待排序記錄已經排好序,第一趟經過n-1次比較後第一個記錄保持位置不變,並得到一個n-1個元素的子記錄;第二趟經過n-2次比較,將第二個記錄定位在原來的位置上,並得到一個包括n-2個記錄的子檔案,依次類推,這樣總的比較次數是:
示例程式碼:
//a:待排序陣列,low:最低位的下標,high:最高位的下標
void quickSort(int a[],int low, int high)
{
if(low>=high)
{
return;
}
int left=low;
int right=high;
int key=a[left]; /*用陣列的第一個記錄作為分割槽元素*/
while(left!=right){
while(left<right&&a[right]>=key) /*從右向左掃描,找第一個碼值小於key的記錄,並交換到key*/
--right;
a[left]=a[right];
while(left<right&&a[left]<=key)
++left;
a[right]=a[left]; /*從左向右掃描,找第一個碼值大於key的記錄,並交換到右邊*/
}
a[left]=key; /*分割槽元素放到正確位置*/
quickSort(a,low,left-1);
quickSort(a,left+1,high);
}- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22

- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
2.2插入類排序
插入排序的基本方法是:每步將一個待排序的記錄,按其排序碼大小,插到前面已經排序的檔案中的適當位置,直到全部插入完為止。
2.2.1直接插入排序
原理:從待排序的n個記錄中的第二個記錄開始,依次與前面的記錄比較並尋找插入的位置,每次外迴圈結束後,將當前的數插入到合適的位置。
穩定性:穩定排序。
時間複雜度: O(n)至O(n2)。
最好情況:當待排序記錄已經有序,這時需要比較的次數是Cmin=n−1=O(n)。
最壞情況:如果待排序記錄為逆序,則最多的比較次數為Cmax=∑i=1n−1(i)=n(n−1)2=O(n2)。
示例程式碼:
//A:輸入陣列,len:陣列長度
void insertSort(int A[],int len)
{
int temp;
for(int i=1;i<len;i++)
{
int j=i-1;
temp=A[i];
//查詢到要插入的位置
while(j>=0&&A[j]>temp)
{
A[j+1]=A[j];
j--;
}
if(j!=i-1)
A[j+1]=temp;
}
}- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18

- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
2.2.2 Shell排序
Shell 排序又稱縮小增量排序, 由D. L. Shell在1959年提出,是對直接插入排序的改進。
原理: Shell排序法是對相鄰指定距離(稱為增量)的元素進行比較,並不斷把增量縮小至1,完成排序。
Shell排序開始時增量較大,分組較多,每組的記錄數目較少,故在各組內採用直接插入排序較快,後來增量di分組排序,檔案叫接近於有序狀態,所以新的一趟排序過程較快。因此Shell排序在效率上比直接插入排序有較大的改進。
在直接插入排序的基礎上,將直接插入排序中的1全部改變成增量d即可,因為Shell排序最後一輪的增量d就為1。
穩定性:不穩定排序。
時間複雜度:O(n1.3)。
對於增量的選擇,Shell 最初建議增量選擇為n/2,並且對增量取半直到 1;D. Knuth教授建議di+1=⌊di−13⌋序列。
//A:輸入陣列,len:陣列長度,d:初始增量(分組數)
void shellSort(int A[],int len, int d)
{
for(int inc=d;inc>0;inc/=2){ //迴圈的次數為增量縮小至1的次數
for(int i=inc;i<len;++i){ //迴圈的次數為第一個分組的第二個元素到陣列的結束
int j=i-inc;
int temp=A[i];
while(j>=0&&A[j]>temp)
{
A[j+inc]=A[j];
j=j-inc;
}
if((j+inc)!=i)//防止自我插入
A[j+inc]=temp;//插入記錄
}
}
}- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17

- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
注意:從程式碼中可以看出,增量每次變化取前一次增量的一般,當增量d等於1時,shell排序就退化成了直接插入排序了。
2.3選擇類排序
選擇類排序的基本方法是:每步從待排序記錄中選出排序碼最小的記錄,順序放在已排序的記錄序列的後面,知道全部排完。
2.3.1簡單選擇排序(又稱直接選擇排序)
原理:從所有記錄中選出最小的一個數據元素與第一個位置的記錄交換;然後在剩下的記錄當中再找最小的與第二個位置的記錄交換,迴圈到只剩下最後一個數據元素為止。
穩定性:不穩定排序。
時間複雜度: 最壞、最好和平均複雜度均為O(n2)。
示例程式碼:
void selectSort(int A[],int len)
{
int i,j,k;
for(i=0;i<len;i++){
k=i;
for(j=i+1;j<len;j++){
if(A[j]<A[k])
k=j;
}
if(i!=k){
A[i]=A[i]+A[k];
A[k]=A[i]-A[k];
A[i]=A[i]-A[k];
}
}
}- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16

- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
2.3.2堆排序
直接選擇排序中,第一次選擇經過了n-1次比較,只是從排序碼序列中選出了一個最小的排序碼,而沒有儲存其他中間比較結果。所以後一趟排序時又要重複許多比較操作,降低了效率。J. Willioms和Floyd在1964年提出了堆排序方法,避免這一缺點。
堆的性質:
(1)性質:完全二叉樹或者是近似完全二叉樹;
(2)分類:大頂堆:父節點不小於子節點鍵值,小頂堆:父節點不大於子節點鍵值;圖展示一個最小堆:
(3)左右孩子:沒有大小的順序。
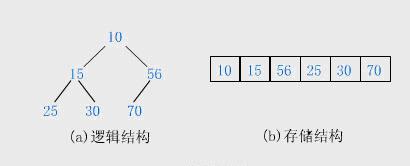
(4)堆的儲存
一般都用陣列來儲存堆,i結點的父結點下標就為(i–1)/2。如第0個結點左右子結點下標分別為1和2。
(5)堆的操作
建立:
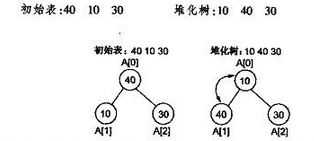
以最小堆為例,如果以陣列儲存元素時,一個數組具有對應的樹表示形式,但樹並不滿足堆的條件,需要重新排列元素,可以建立“堆化”的樹。
插入:
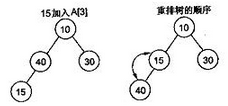
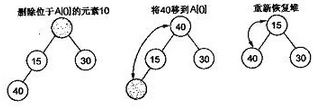
將一個新元素插入到表尾,即陣列末尾時,如果新構成的二叉樹不滿足堆的性質,需要重新排列元素,下圖演示了插入15時,堆的調整。
刪除:
堆排序中,刪除一個元素總是發生在堆頂,因為堆頂的元素是最小的(小頂堆中)。表中最後一個元素用來填補空缺位置,結果樹被更新以滿足堆條件。
穩定性:不穩定排序。
插入程式碼實現:
每次插入都是將新資料放在陣列最後。可以發現從這個新資料的父結點到根結點必然為一個有序的數列,現在的任務是將這個新資料插入到這個有序資料中,這就類似於直接插入排序中將一個數據併入到有序區間中,這是節點“上浮”調整。不難寫出插入一個新資料時堆的調整程式碼:
//新加入i結點,其父結點為(i-1)/2
//引數:a:陣列,i:新插入元素在陣列中的下標
void minHeapFixUp(int a[], int i)
{
int j, temp;
temp = a[i];
j = (i-1)/2; //父結點
while (j >= 0 && i != 0)
{
if (a[j] <= temp)//如果父節點不大於新插入的元素,停止尋找
break;
a[i]=a[j]; //把較大的子結點往下移動,替換它的子結點
i = j;
j = (i-1)/2;
}
a[i] = temp;
} - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17

- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
因此,插入資料到最小堆時:
//在最小堆中加入新的資料data
//a:陣列,index:插入的下標,
void minHeapAddNumber(int a[], int index, int data)
{
a[index] = data;
minHeapFixUp(a, index);
} - 1
- 2
- 3
- 4
- 5
- 6
- 7

- 1
- 2
- 3
- 4
- 5
- 6
- 7
刪除程式碼實現:
按定義,堆中每次都只能刪除第0個數據。為了便於重建堆,實際的操作是將陣列最後一個數據與根結點,然後再從根結點開始進行一次從上向下的調整。
調整時先在左右兒子結點中找最小的,如果父結點不大於這個最小的子結點說明不需要調整了,反之將最小的子節點換到父結點的位置。此時父節點實際上並不需要換到最小子節點的位置,因為這不是父節點的最終位置。但邏輯上父節點替換了最小的子節點,然後再考慮父節點對後面的結點的影響。相當於從根結點將一個數據的“下沉”過程。下面給出程式碼:
//a為陣列,從index節點開始調整,len為節點總數 從0開始計算index節點的子節點為 2*index+1, 2*index+2,len/2-1為最後一個非葉子節點
void minHeapFixDown(int a[],int len,int index){
if(index>(len/2-1))//index為葉子節點不用調整
return;
int tmp=a[index];
int lastIndex=index;
while(index<=(len/2-1)){ //當下沉到葉子節點時,就不用調整了
if(a[2*index+1]<tmp) //如果左子節點大於該節點
lastIndex = 2*index+1;
//如果存在右子節點且大於左子節點和該節點
if(2*index+2<len && a[2*index+2]<a[2*index+1]&& a[2*index+2]<tmp)
lastIndex = 2*index+2;
if(lastIndex!=index){ //如果左右子節點有一個小於該節點則設定該節點的下沉位置
a[index]=a[lastIndex];
index=lastIndex;
}else break; //否則該節點不用下沉調整
}
a[lastIndex]=tmp;//將該節點放到最後的位置
}- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19

- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
根據思想,可以有不同版本的程式碼實現,以上是和孫凜同學一起討論出的一個版本,在這裡感謝他的參與,讀者可另行給出。個人體會,這裡建議大家根據對堆調整的過程的理解,寫出自己的程式碼,切勿看示例程式碼去理解演算法,而是理解演算法思想寫出程式碼,否則很快就會忘記。
建堆:
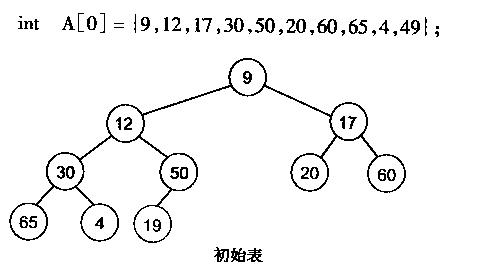
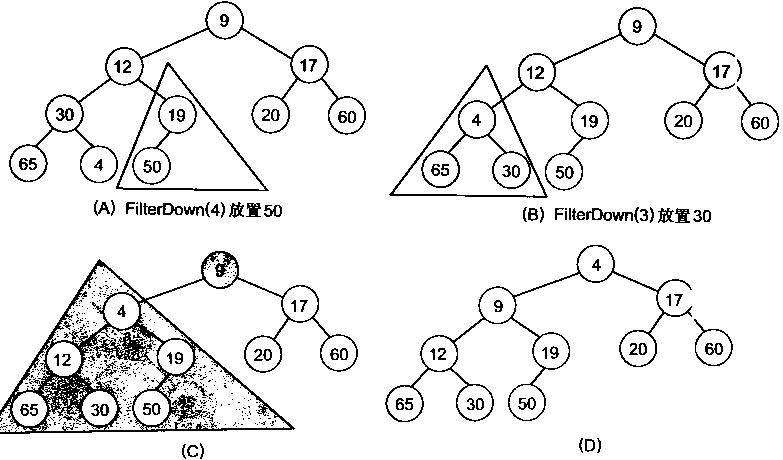
有了堆的插入和刪除後,再考慮下如何對一個數據進行堆化操作。要一個一個的從陣列中取出資料來建立堆吧,不用!先看一個數組,如下圖:
很明顯,對葉子結點來說,可以認為它已經是一個合法的堆了即20,60, 65, 4, 49都分別是一個合法的堆。只要從A[4]=50開始向下調整就可以了。然後再取A[3]=30,A[2] = 17,A[1] = 12,A[0] = 9分別作一次向下調整操作就可以了。下圖展示了這些步驟:
寫出堆化陣列的程式碼:
//建立最小堆
//a:陣列,n:陣列長度
void makeMinHeap(int a[], int n)
{
for (int i = n/2-1; i >= 0; i--)
minHeapFixDown(a, i, n);
} - 1
- 2
- 3
- 4
- 5
- 6
- 7

- 1
- 2
- 3
- 4
- 5
- 6
- 7
(6)堆排序的實現
由於堆也是用陣列來儲存的,故對陣列進行堆化後,第一次將A[0]與A[n - 1]交換,再對A[0…n-2]重新恢復堆。第二次將A[0]與A[n – 2]交換,再對A[0…n - 3]重新恢復堆,重複這樣的操作直到A[0]與A[1]交換。由於每次都是將最小的資料併入到後面的有序區間,故操作完成後整個陣列就有序了。有點類似於直接選擇排序。
因此,完成堆排序並沒有用到前面說明的插入操作,只用到了建堆和節點向下調整的操作,堆排序的操作如下:
//array:待排序陣列,len:陣列長度
void heapSort(int array[],int len){
//建堆
makeMinHeap(array, len);
//根節點和最後一個葉子節點交換,並進行堆調整,交換的次數為len-1次
for(int i=0;i<len-1;++i){
//根節點和最後一個葉子節點交換
array[0] += array[len-i-1];
array[len-i-1] = array[0]-array[len-i-1];
array[0] = array[0]-array[len-i-1];
//堆調整
minHeapFixDown(array, 0, len-i-1);
}
} - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15

- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
(7)堆排序的效能分析
由於每次重新恢復堆的時間複雜度為O(logN),共N - 1次堆調整操作,再加上前面建立堆時N / 2次向下調整,每次調整時間複雜度也為O(logN)。兩次次操作時間相加還是O(N * logN)。故堆排序的時間複雜度為O(N * logN)。
最壞情況:如果待排序陣列是有序的,仍然需要O(N * logN)複雜度的比較操作,只是少了移動的操作;
最好情況:如果待排序陣列是逆序的,不僅需要O(N * logN)複雜度的比較操作,而且需要O(N * logN)複雜度的交換操作。總的時間複雜度還是O(N * logN)。
因此,堆排序和快速排序在效率上是差不多的,但是堆排序一般優於快速排序的重要一點是,資料的初始分佈情況對堆排序的效率沒有大的影響。
2.4歸併排序
演算法思想:
歸併排序屬於比較類非線性時間排序,號稱比較類排序中效能最佳者,在資料中應用中較廣。
歸併排序是分治法(Divide and Conquer)的一個典型的應用。將已有序的子序列合併,得到完全有序的序列;即先使每個子序列有序,再使子序列段間有序。若將兩個有序表合併成一個有序表,稱為二路歸併。
穩定性:穩定排序演算法;
時間複雜度: 最壞,最好和平均時間複雜度都是Θ(nlgn)。
2.5線性時間非比較類排序
2.5.1計數排序
計數排序是一個非基於比較的排序演算法,該演算法於1954年由 Harold H. Seward 提出,它的優勢在於在對於較小範圍內的整數排序。它的複雜度為Ο(n+k)(其中k是待排序數的範圍),快於任何比較排序演算法,缺點就是非常消耗空間。很明顯,如果而且當O(k)>O(n*log(n))的時候其效率反而不如基於比較的排序,比如堆排序和歸併排序和快速排序。
演算法原理:
基本思想是對於給定的輸入序列中的每一個元素x,確定該序列中值小於x的元素的個數。一旦有了這個資訊,就可以將x直接存放到最終的輸出序列的正確位置上。例如,如果輸入序列中只有17個元素的值小於x的值,則x可以直接存放在輸出序列的第18個位置上。當然,如果有多個元素具有相同的值時,我們不能將這些元素放在輸出序列的同一個位置上,在程式碼中作適當的修改即可。
演算法步驟:
(1)找出待排序的陣列中最大的元素;
(2)統計陣列中每個值為i的元素出現的次數,存入陣列C的第i項;
(3)對所有的計數累加(從C中的第一個元素開始,每一項和前一項相加);
(4)反向填充目標陣列:將每個元素i放在新陣列的第C(i)項,每放一個元素就將C(i)減去1。
時間複雜度:Ο(n+k)。
空間複雜度:Ο(k)。
要求:待排序數中最大數值不能太大。
穩定性:穩定。
程式碼示例:
#define MAXNUM 20 //待排序數的最大個數
#define MAX 100 //待排序數的最大值
int sorted_arr[MAXNUM]={0};
相關推薦
八種常見排序演算法的比較和實現
首先排序演算法大的可以分為:
1、關鍵字比較 2、非關鍵字比較
關鍵字比較 關鍵字比較就是通過關鍵字之間的比較和移動,從而使整個序列有序, 而關鍵字比較的演算法,又可以像下面這樣劃分:
對於排序演算法之間的比較,無異於時間複雜度和空間複雜度。
從上表可以看出: 1、從平均時
十大常見排序演算法
一、排序演算法概述
排序演算法最常用操作:交換元素
public void sort(int[] arr, int i, int j){
int temp = arr[i];
arr[i] = arr[j];
arr[j]
資料結構(一):幾種常見排序演算法比較
排序
0. 常見排序演算法效率比較
時間複雜度及穩定性比較
排序方法
平均方法
最優複雜度
最壞複雜度
輔助空間
穩定性
氣泡排序
O(
幾種常見排序演算法及其效率
介紹了幾種交換排序的演算法
1。氣泡排序(Bubble Sort)是一種簡單的排序演算法。它重複地走訪過要排序的數列,一次比較兩個元素,如果他們的順序錯誤就把他們交換過來。走訪數列的工作是重複地進行直到沒有再需要交換,也就是說該數列已經排序完成。這個演算法的名字由來是因為越小的元素會經由交換慢慢“浮”到數列
自己整理的幾種常見排序演算法,及時間複雜度空間複雜度。c++程式設計
/*****************************************************
copyright (C), 2014-2015, Lighting Studio. Co., Ltd.
File name:
Author:fhb
六種常見排序演算法Java實現
一、氣泡排序
氣泡排序實現簡單,但執行效率較慢。演算法思想是,設要排序的為陣列A中的元素,遍歷A.length-1次,每次找出待排序元素中最小的值放在相應位置,如:第一次遍歷陣列下標為A.length-1 到0的元素,將最小的值放在A[0]的位置,第二次遍歷
C語言中冒泡法、選擇法、插入法三種常見排序演算法分析
一、冒泡法(起泡法)
演算法要求:用起泡法對10個整數按升序排序。
演算法分析:如果有n個數,則要進行n-1趟比較。在第1趟比較中要進行n-1次相鄰元素的兩兩比較,在第j趟比較中要進行n-j次兩兩比較。比較的順序從前往後,經過一趟比較後,將最值沉底(換到最後一個元
幾種常見排序演算法java實現
public class sort {
public static void main(String[] args) {
int[] a= {10,1,35,14,9,12,11};
int c=(int)Math.floor(Math.random()*7);
7種常見排序演算法的c++實現
今天心血來潮複習了一下基本的排序演算法,實現了一下,就順便發上來咯。。在程式碼裡做了註釋了-。-也就不多說了,直接上程式碼吧。。// order_algorithm.cpp: 定義控制檯應用程式的入口點。
//author: netbin
#include "stdafx.
1T資料快速排序!十種經典排序演算法總結
# 1 氣泡排序
每次迴圈都比較前後兩個元素的大小,如果前者大於後者,則將兩者進行交換。這樣做會將每次迴圈中最大的元素替換到末尾,逐漸形成有序集合。將每次迴圈中的最大元素逐漸由隊首**轉移**到隊尾的過程形似“冒泡”過程,故因此得名。
一個優化氣泡排序的方法就是如果在一次迴圈的過程中沒有發生交換,則可以立
十種常見的排序演算法
1.常見演算法分類
十種常見排序演算法一般分為以下幾種:
(1)非線性時間比較類排序:交換類排序(快速排序和氣泡排序)、插入類排序(簡單插入排序和希爾排序)、選擇類排序(簡單選擇排序和堆排序)、歸併排序(二路歸併排序和多路歸併排序);
(2)線性時間非比較類排序:計數排序、基數排序和桶排序。
總結:
八種常見的演算法排序
一、排序演算法的分類(列舉7種):
1.氣泡排序
2.選擇排序
3.插入排序
4.快速排序
5.歸併排序 (歸併排序需要額外的記憶體空間來儲存資料,其他的方式都是在原來資料上做交換)
6.希爾排序
7.堆排序
1、最基礎的排序——氣泡排序 (時間複雜度
常見14種經典排序演算法(Java程式碼實現)
尊重原創,轉載請標明出處 http://blog.csdn.net/abcdef314159 ,想了解更多演算法題可以關注微信公眾號“資料結構和演算法”,每天一題為你精彩解答。
一,氣泡排序
排序演算法其實有很多,氣泡排序基本上算是最簡單的一種
Python的十種常見演算法
十種排序演算法
1. 常見演算法分類
十種常見排序演算法一般分為以下幾種:
(1)非線性時間比較類排序:
a. 交換類排序(快速排序、氣泡排序)
b. 插入類排序(簡單插入排序、希爾排序)
c. 選擇類排序(簡單選擇排序、堆排序)
d. 歸併排序(二路歸併排序、多路歸併排序)
常見的幾種內排序演算法以及實現(C語言)
所有未排序的陣列是經過檢查合法的
主要的內排序包括冒泡、插入、希爾、堆排序、歸併、快速、桶排序等
其C語言實現的原始檔下載地址:http://download.csdn.net/detail/mcu_tian/9530227
氣泡排序
氣泡排序應該是排序中最簡單的演算法了
【知了堂學習筆記】java 編寫幾種常見排序算法
第一個 public 調用 ati print 所有 eth string quick 排序的分類:
一.交換排序
所謂交換,就是根據序列中兩個記錄鍵值的比較結果來對換這兩個記錄在序列中的位置,交換排序的特點是:將鍵值較大的記錄向序列的尾部移動,鍵值較小的記錄向序列的前部
php實現7種常見排序
tar AI eap continue nds UNC reat pub HP
class test{
public function main()
{
$data = $this->createData();
$th
7種常見排序算法
算法 元素 歸並排序 最後一個元素 中間 刪除 二叉 節點 個數 1. 冒泡排序從第一個元素開始與右側元素兩兩比較並交換,直到右側成為有序部分。
2. 選擇排序有序部分在左側,在剩余元素中找到最小的那個元素,並與剩余元素中第一個元素交換。
3. 插入排序有序部分在左側,將剩
常見排序演算法之歸併排序
文章目錄
常見排序演算法之歸併排序
原地歸併方法
自頂向下的歸併排序
自底向上的歸併排序
特點
複雜度分析
參考資料
常見排序演算法之歸併排序
原地歸併方法
該方法將兩個不同的
十大經典排序演算法(動圖演示) 十大經典排序演算法(動圖演示)
十大經典排序演算法(動圖演示)
0、演算法概述
0.1 演算法分類
十種常見排序演算法可以分為兩大類:
非線性時間比較類排序:通過比較來決定元素間的相對次序,由於其時間複雜度不能突破O(nlogn),因此稱為非線性時間比較類排序。
線性