一.再看線性迴歸

之前我們選擇線性迴歸的時候，只是認為那些資料看上去很符合線性的樣子，選擇最小平方損失函式的時候，也是直接提出來的，沒有考慮過為什麼會是這個樣子。接下來就從概率的角度來解釋這些問題。
首先假設目標變數和輸入與下面這個方程相關：

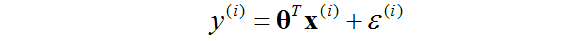
其中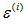是一個誤差項（error term），來捕捉一些我們建模的時候故意或者無意忽略但是對於預測有影響的因素。有時候也可以作為一個隨機的噪聲（random noise）。“誤差項（噪聲項）”的引入允許我們獲得引數值和預測的置信程度。
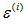
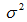
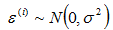
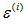
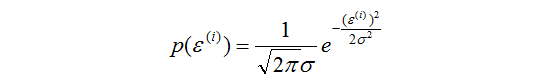
我們進一步假設獨立同分布且服從均值為0，方差為高斯分佈，那麼我們能夠把這個假設寫為，即的概率密度是：

那麼根據高斯分佈的性質，這時候的輸出y也是一個隨機變數。且有

，即：

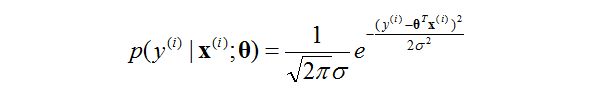
這裡提示一下，很重要的一個記號，在論文裡面經常看見。表示θ做引數，隨機變數下的分佈。
這裡再提示一下，連續隨機變數密度函式上的取值並不代表概率。連續隨機變數在每一點上面的概率都是0。這是基礎知識，別忘了。要是密度函式上面A點的值很大，B點的值很小。只能夠說明在A點附近的可能性很大。也就是說，雖然在某點上的概率是多少是錯的，但是我們還是需要在密度函式上面找最值，因為這個點“附近”的概率是最大的。

一般來說，我們感興趣的並不是單個數據點的似然值，而是整個資料集上面所有點的似然值。要是有m個數據點，我們感興趣的就是他們的聯合條件密度，且因為各自獨立，有：

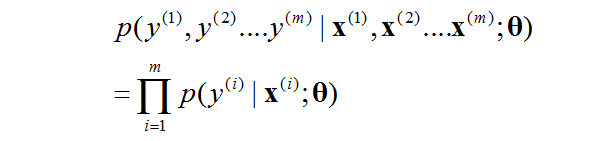
上面那個記號就是聯合條件密度的記號，不要在其中想太多。
寫成向量更緊縮的形式：

其中，

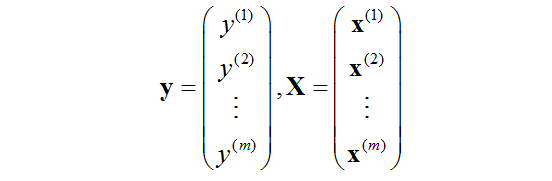
同樣也僅僅是寫的更加簡潔一點，也別在上面想太多。
令：

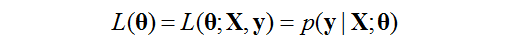
我們把這個函式叫做似然函式（likelihood function），是以θ為變數的函式。
通過前面的原理可以知道

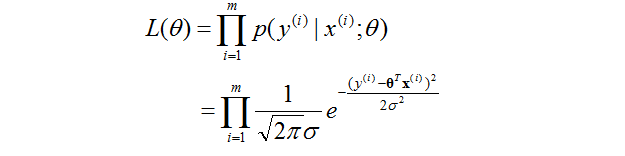
本質就是把之前的幾個公式代進去了而已，不用解釋了。
這個公式的意思也很容易理解。怎麼選擇θ使得整個似然函式有最大的值，也就是讓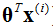更加接近於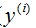。這個地方有點難想，多理解幾遍。
學過概率論的都知道，接下來要對數化一下，使得方程更加容易解出來。沒有什麼技巧，暴力推導如下：

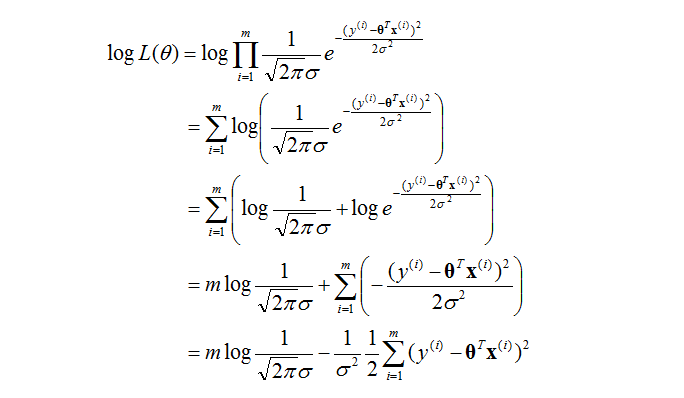
我們的目的是要大化L(θ),那麼只需要最小化

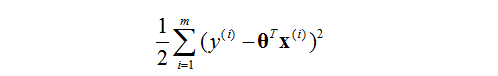
這個函式就行了。
對於這個函式是不是有點眼熟呢？就是之前的最小均方誤差了。
因為這裡是這種形式，剛好和之前的是反的。所以在用梯度法求的時候，就不是梯度下降法了，而是梯度上升法。
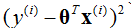
到這裡，對於線性迴歸的回顧就到這裡了，這裡引出了概率的方法來做機器學習的推導，對於理解下面的logistic的推導是有幫助的。

二.logistic迴歸

Ⅰ.背景

logistic迴歸是非常進經典的分類的方法，分類問題在第一個筆記有詳細的介紹。他和迴歸的區別就是他的y值是離散的值，比如有3個類，分別是0類，1類和2類這樣子。
我們這裡討論的分類問題主要是2分類問題，就是最後的結果只有兩類，姑且定做0類（負類）和1類（正類）。那麼y的值就為0或者1。
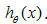
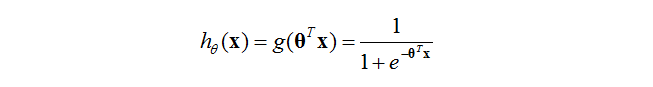
把hypotheses 改寫成另外的形式

其中

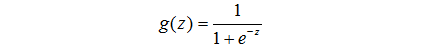
這個函式就叫做logistic函式或者sigmoid函式

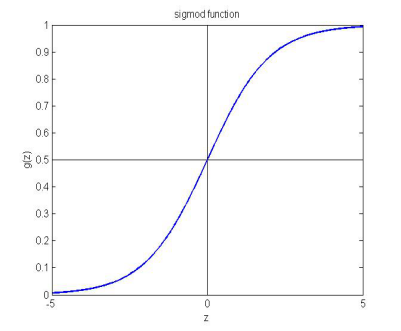
當的時候,sigmoid函式值為0.5.然後隨著z的值越大,函式越趨向於1;隨著x的值越小,x的值越趨向於0.
因為這樣,那麼當一個數據丟進sigmoid函式中得到的值大於0.5,那麼就可以把它歸為1類.反之,當得到的值小於0.5,那麼就把它歸為0類.
最終，不管你丟進去什麼值，最終的結果就會在0和1之間。
然後這個函式的導數可以很容易推得

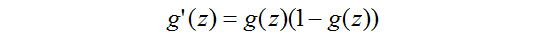
這個性質很重要，不管是在計算裡面還是在證明裡面。

Ⅱ.梯度下降學習

首先我們假設

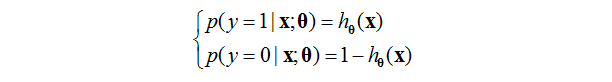
這個限制表示有且只會有兩個結果。
上面的可以寫為

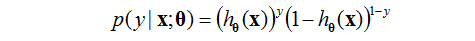
假設我們提供的訓練的例子都是獨立同分布的。我們能夠寫出似然函式為：

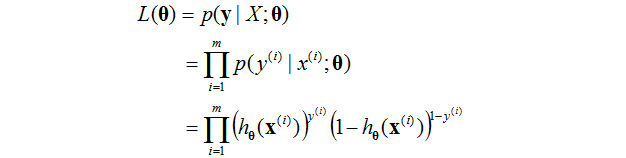
對數似然函式為：

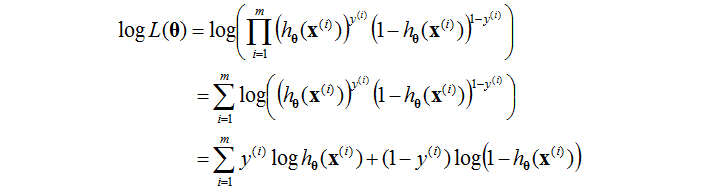
之前我們說過，我們想要得到引數的表示式，需要最大化（對數）似然函式。
如果你數學足夠好的話，你也許能夠手推上面這個似然函式的最值。但是，這幾乎是沒有意義的。
我們可以使用梯度上升的方法來逼近近似，這是計算機容易實現的，擴充套件性比手算要好的方式。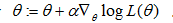
那麼問題就轉化為怎麼算出某個的偏導。
暴力手推：

在上面的推導中，用到了前面提到的那個logistic函式導數的公式。
最終的梯度更新公式為

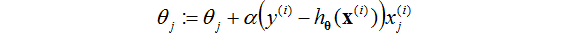
這個更新公式和線性迴歸的公式是差不多的。

Ⅲ.例子