手眼標定問題描述

       在機器人校準測量、機器人手眼協調以及機器人輔助測量等領域，都要求知道機器人執行器末端（抓取臂）座標系和感測器（比如用來測量三維空間中目標位置和方向並固定在機器人手上的攝像機）座標系之間的相互關係，確定這種轉換關係在機器人領域就是通常所說的手眼標定。

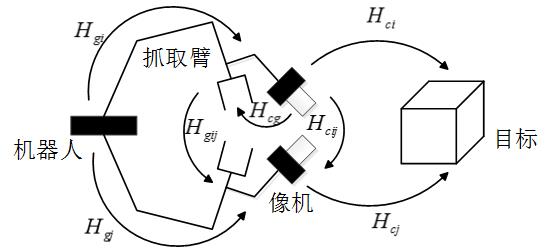
       將手眼標定系統如下圖所示，其中Hgij為機器人執行器末端座標系之間相對位置姿態的齊次變換矩陣；Hcij為攝像機座標系之間相對位置姿態的齊次變換矩陣；Hcg為像機與機器人執行器末端之間的相對位置姿態齊次矩陣。

       經過座標系變換，Hgij、Hcij和Hcg滿足如下關係：

HgijH

cg=HcgHcij⇔(Rgij0Tgij1)(Rcg0Tcg1)=(Rcg0Tcg1)(Rcij0Tcij1)
       將上式展開，可以得到手眼標定的基本方程：
{RgijRcg=RcgRcij(Rgij−I)Tcg=RcgTcij−Tgij
       因此，手眼標定問題也就轉化為從上述方程組中求解出Rcg和Tcg，下面就按照TSAI文獻所述求解該方程組。

“兩步法”手眼標定

       一般用“兩步法”求解基本方程，即先從基本方程上式求解出Rcg，再代入下式求解出Tcg。在TSAI文獻中引入旋轉軸-旋轉角系統來描述旋轉運動來進行求解該方程組，具體的公式推導可以檢視原始文獻，這裡只歸納計算步驟，不明白的地方可閱讀文獻，計算步驟如下：

Step1：利用羅德里格斯變換將旋轉矩陣轉換為旋轉向量

{rgij=rodrigues(Rgij)rcij=rodrigues(Rcij)

Step2：向量歸一化

⎧⎩⎨⎪⎪⎪⎪⎪⎪θgij=∥∥rgij∥∥2Nr

相關推薦

經典手眼標定演算法之Tsai-Lenz的OpenCV實現

手眼標定問題描述        在機器人校準測量、機器人手眼協調以及機器人輔助測量等領域，都要求知道機器人執行器末端（抓取臂）座標系和感測器（比如用來測量三維空間中目標位置和方向並固定在機器人手上的攝像機）座標系之間的相互關係，確定這種轉換關係在機器人

經典整合學習演算法和部分python實現

Boosting Boosting的大概思想是先從初始訓練集中訓練出一個基學習器，再根據這個基學習器對訓練集的判斷重新調整訓練集，讓當前分類器判斷錯誤的樣本在後續學習中受到更高的關注，如此不斷迭代，直到生成目標數目的基學習器，然後根據權重相加，獲得一個強學習器

合婚演算法之用JAVA實現本命卦合婚法

  問題:我輸入 男方的生日:1980-01-01  01:01:01 女方生日：1980-01-01  01:01:01    跪求這樣一個八字合婚演算法    合婚軟體似乎很多，關鍵是怎麼去寫或者說演算法，網路上幾乎沒有類似文章   作為易學高手的我（大師♂羅莊）對告

【乾貨】10道經典的java演算法之面試題

對於演算法題，大家都很熟悉，無論在企業中還是在面試的時候，演算法依然是考研我們的一個標準. 根據實際情況，大家可能會認為 公司裡幾乎用不到演算法。我覺得這種說法是片面的。我們在熟練寫一段程式碼的時候，如果對其進行用優雅的方式實現出來，這就是演算法。個人對演算法的理解： 演算法只是解決問題

手眼標定演算法---Navy演算法（Robot sensor calibration: solving AX=XB on the Euclidean group）

本文主要介紹Frank C. Park and Bryan J. Martin在文獻Robot sensor calibration: solving AX=XB on the Euclidean group中提出的手眼標定演算法，該演算法也被稱為Navy手眼標定演算法，該演算法的主要創新點為利用李

手眼標定演算法---Sai-Lenz(A New Technique for Fully Autonomous and Efficient 3D Robotics Hand/Eye Calibrati)

 本文主要是講解經典手眼標定問題中的TSAI-LENZ 文獻方法，參考文獻為“A New Technique for Fully Autonomous and Efficient 3D Robotics Hand/Eye Calibration”  轉自：https://blog

八字易經演算法之用JAVA實現 地藏十神排法

  序：我們的排盤系統基本做好了。就剩下兩個問題 地藏十神排法 大運起始或者說幾歲上運演算法了   需要的文章：   這裡說下就可以了      地支藏幹 子藏癸 卯藏乙 午藏丁己  酉藏辛             寅藏 甲丙戊  巳藏 丙庚戊  申藏 庚壬戊 

BP神經網路演算法之matlab具體實現

之前的幾篇部落格的一個共同點就是梯度下降法，梯度下降法是用來求解無約束最優化問題的一個數值方法，簡單實用，幾乎是大部分演算法的基礎，下面來利用梯度下降法優化BP神經網路。 [TOC] 梯度公式 下面的BP神經網路結構為最簡單的三層網路，各層的神經元數量

資料結構演算法之C語言實現

單鏈表演算法大全（包含所有常見操作）：單鏈表演算法連結 二叉樹演算法大全（包含所有常見操作）：二叉樹演算法連結 矩陣無向圖演算法（生成、BFS、DFS）：矩陣無向圖演算法連結 鄰接表無向圖

考研資料結構與演算法之利用堆疊實現行編輯程式

今天我的部落格終於迎來了第一位關注著，但是同時我也發現了之前的程式在出棧時是有一些問題的，但是還沒找到確切的原因，然後這一段程式碼是今天晚上實現的行編輯的demo，但是現在是不完善的，明天或者後天我將會將它徹底修復。 #include <stdio.h> #i

排序演算法之——優先佇列經典實現（基於二叉堆）

許多應用都需要處理有序的元素，但有時，我們不要求所有元素都有序，或是一定要一次就將它們排序，許多情況下，我們會收集這些元素裡的最大值或最小值。 這種情況下一個合適的資料結構應該支援兩種操作：插入元素、刪除最大元素。 優先佇列與棧和佇列類似，但它有自己的奇妙之處。 在本文中，會講解基於二叉堆的一種優先佇列

經典演算法研究系列 九之續 sift演算法的編譯與實現

                九之續、sift演算法的編譯與實現作者：July 、二零一一年三月一日。程式碼：Rob Hess維護的sift 庫，July updated。環境：windows xp+vc6.0。條件：opencv1.0、gsl-1.8.exe------------------------

經典演算法之希爾排序（三種實現）

希爾排序的實質就是分組插入排序，該方法又稱縮小增量排序，因DL．Shell於1959年提出而得名。 該方法的基本思想是：先將整個待排元素序列分割成若干個子序列（由相隔某個“增量”的元素組成的）分別進行直接插入排序，然後依次縮減增量再進行排序，待整個序列中的元素

經典演算法之歸併排序的C實現方法

以前寫過歸併排序的演算法，但是時間過了好久，忘記怎麼寫的了，（也是醉了）。正好複習演算法的時候遇到這個問題，就重新寫了一下，把遇到的一些問題順便記錄一下。 核心就是用兩個子陣列記錄分割後的兩個陣列中的變數， 然後依次比較大小即可。 這裡有個細節需要注意一下，

經典演算法之非遞迴演算法實現二叉樹前、中、後序遍歷

/************************ author's email:[email protected] date:2017.12.24 非遞迴演算法實現二叉樹前、中、後序遍歷 ************************/ #include<

聚類演算法之DBSCAN演算法之一：經典DBSCAN

DBSCAN是基於密度空間的聚類演算法，與KMeans演算法不同，它不需要確定聚類的數量，而是基於資料推測聚類的數目，它能夠針對任意形狀產生聚類。 1.epsilon-neighborhood epsoiln-neighborhood(簡稱e-nbhd）可理解為密度空間，表示半徑為e

經典排序演算法之--選擇排序

瞭解了前兩種排序演算法，再來看選擇排序已經很簡單了，它的思路是：       從一堆序列中，選擇一個最小的數，作為新的有序序列的頭，剩下的元素依次重複這一過程。 核心程式碼如下： for(int i=0;i<a.length;i++

經典排序演算法之--快速排序

快速排序是一種高效但不穩的排序演算法，不穩性取決於比較基數的選擇帶有隨機性，其排序原理應用百度百科如下： 設要排序的陣列是A[0]……A[N-1]，首先任意選取一個數據（通常選用陣列的第一個數）作為關鍵資料，然後將所有比它小的數都放到它前面，所有比它大的數都放到它後面，這個過程稱為一趟快速排

c#程式碼實現排序演算法之歸併排序

歸併排序的平均時間複雜度為O(nlogn)，最好時間複雜度為O(nlogn)，最壞時間複雜度為O(nlogn)，空間複雜度為O(n)，是一種穩定的演算法。 1.將待排序序列r(1)，r(2)，…，r(n)劃分為兩個長度相等的子序列r(1)，…r(n/2)和r(n/2+1)，…，r

c#程式碼實現排序演算法之快速排序

快速排序的平均時間複雜度為O（nlog2n），最好時間複雜度為O（nlog2n），最壞時間複雜度為O（n²），空間複雜度為O（log2n），是一種不穩定的演算法。 1.劃分：選定一個記錄作為軸值，以軸值為基準將整個序列劃分為兩個子序列r(1)…r(i-1)和r(i+1)…r(n)