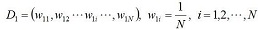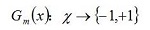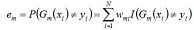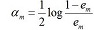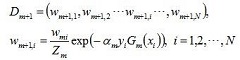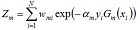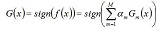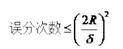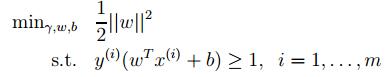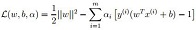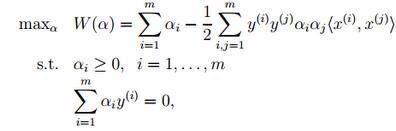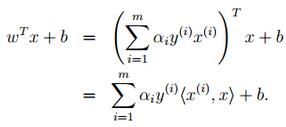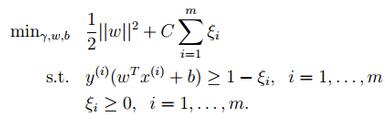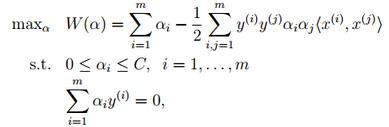機器學習常見演算法總結(二)
5. Adaboost
adaboost演算法通俗地講,就是在一個數據集上的隨機資料使用一個分類訓練多次,每次對分類正確的資料賦權值較小,同時增大分類錯誤的資料的權重,如此反覆迭代,直到達到所需的要求。Adaboost演算法步驟如下:
步驟1. 首先初始化訓練資料的權值分佈,每一個訓練樣本開始時被賦予相同的權重:1/N。
步驟2. 進行多輪迭代,用m=1,2,3,…,M表示迭代的第多少輪
a. 使用權值分佈Dm的訓練資料集學習,得到基本分類器
b. 計算Gm(x)在訓練資料集上的分類誤差率
由上述公式可得:Gm(x)在訓練資料集上的誤分率em=被Gm(x)誤分類樣本的權值之和。
c. 計算Gm(x)係數,am表示Gm(x)在最終分類器中的重要程度
當em<=1/2時am>=0,且am隨著em的減小而增大,這意味著誤分率越小的基本分類器在最終的分類器中作用越大。
d. 更新訓練資料集的權值分佈,得到新的Dm分佈,使得誤分類樣本權值增加,正確分類樣本權值減小,這樣,adaboost方法聚焦於那些較難分類的樣本上。
其中,Zm為規範化因子,使得Dm+1成為一個概率分佈。步驟3. 組合m個弱分類器
,從而得到級聯強分類器
效能評價
優點:簡單,泛化錯誤率低,可以將不同的分類演算法作為弱分類器,充分考慮每個分類器的權重。
缺點:弱分類器數目不好設定,可以使用交叉驗證確定;資料不平衡導致分類精度下降;訓練比較耗時,每次重新選擇當前分類器最好切分點。
應用領域:模式識別、計算機視覺領域、分類問題。
6. SVM
SVM是基於結構風險(經驗風險和置信風險)最小化的機器學習演算法,支援向量機方法是建立在統計學習理論的VC 維理論和結構風險最小原理基礎上的,根據有限的樣本資訊在模型的複雜性(即對特定訓練樣本的學習精度,Accuracy)和學習能力(即無錯誤地識別任意樣本的能力)之間尋求最佳折衷,以期獲得最好的推廣能力[14](或稱泛化能力)。
- 選擇最大間隔分類器的原因
幾何間隔與樣本的誤分次數間存在關係:
其中的分母就是樣本到分類間隔距離,分子中的R是所有樣本中的最長向量值。 - 演算法流程
- 原始目標函式:
- 引入拉格朗日系數α:
- 將上述的公式採用對偶優化理論可以 轉換為下面的目標函式(約束條件來自於上述的公式對w和b求導):
- 而這個函式可以用常用的優化方法求得α,進而求得w和b。
- 按照道理,svm簡單理論應該到此結束。不過還是要補充一點,即在預測時有:
關於鬆弛變數的引入,因此原始的目標優化公式為:
此時對應的對偶優化公式為:
與前面的相比只是α多了個上界。效能評價及應用領域
- 優點:可用於線性/非線性分類,也可以用於迴歸;低泛化誤差;容易解釋;計算複雜度較低;無區域性極小值問題。(相對於神經網路等演算法);解決小樣本下機器學習問題;可以很好的處理高維資料集。
- 缺點:對引數和核函式的選擇比較敏感;原始的SVM只比較擅長處理二分類問題;對缺失資料敏感;對於核函式的高維對映解釋力不強,尤其是徑向基函式。
- 應用:文字分類、影象識別、主要二分類領域
7. K-Means
K-means演算法是聚類分析中使用最廣泛的演算法之一。它把n個物件根據他們的屬性分為k個聚類以便使得所獲得的聚類滿足:同一聚類中的物件相似度較高;而不同聚類中的物件相似度較小。
Kmeans的計算過程大概表示如下:
- step1. 隨機選擇k個聚類中心. 最終的類別個數<= k
- step2. 計算每個樣本到各個中心的距離
- step3.每個樣本聚類到離它最近的中心
- step4.重新計算每個新類的中心
- step5.重複以上步驟直到滿足收斂要求。(通常就是中心點不再改變或滿足一定迭代次數).
虛擬碼如下:
時間複雜度:O(tKmn),其中,t為迭代次數,K為簇的數目,m為記錄數,n為維數
空間複雜度:O((m+K)n),其中,K為簇的數目,m為記錄數,n為維數
這裡在看一下,K-Means的一些問題:
1. k的選擇
k是使用者自己定義的初始化引數,一般表示資料的一種分佈方式。
2. 距離度量(看KNN)
3. 效能評價:
優點:本演算法確定的K 個劃分到達平方誤差最小。當聚類是密集的,且類與類之間區別明顯時,效果較好。對於處理大資料集,這個演算法是相對可伸縮和高效的,計算的複雜度為O(NKt),其中N是資料物件的數目,t是迭代的次數。一般來說,K遠遠小於N,t遠遠小於N 。
缺點:聚類中心的個數K 需要事先給定,但在實際中這個 K 值的選定是非常難以估計的,很多時候,事先並不知道給定的資料集應該分成多少個類別才最合適;Kmeans需要人為地確定初始聚類中心,不同的初始聚類中心可能導致完全不同的聚類結果。(可以使用Kmeans++演算法來解決)